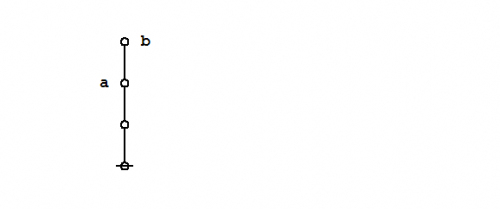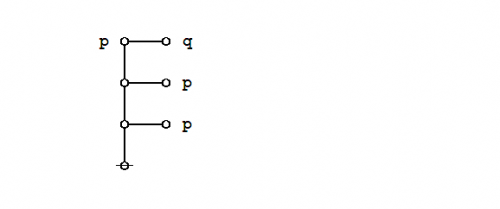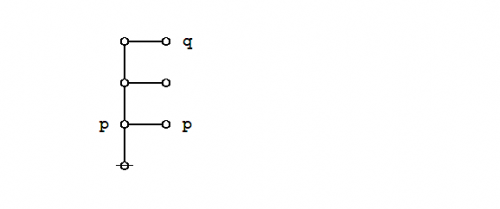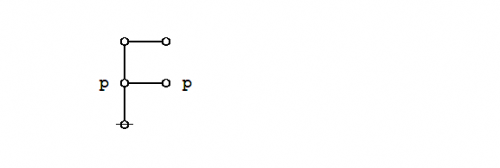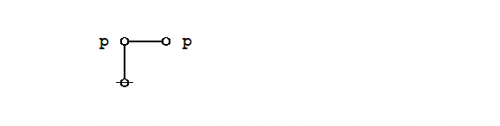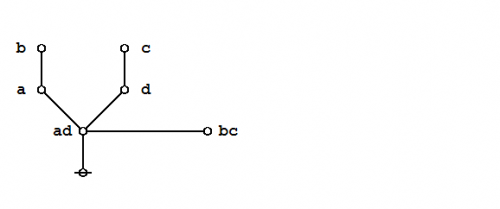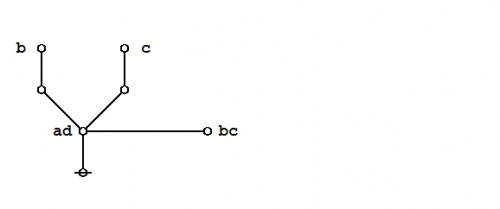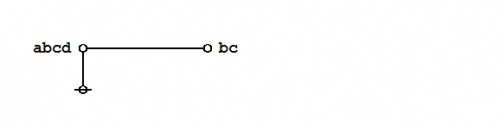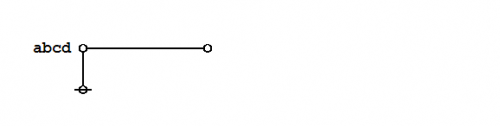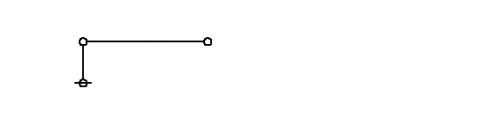Difference between revisions of "Logical graph"
Jon Awbrey (talk | contribs) (→Quick tour of the neighborhood: rework introduction) |
Jon Awbrey (talk | contribs) (spacing in TeX <math>a \texttt{( )} = \texttt{( )},~\!</math>) |
||
| (188 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <font size="3">☞</font> This page belongs to resource collections on [[Logic Live|Logic]] and [[Inquiry Live|Inquiry]]. | |
| − | In his papers on '' | + | A '''logical graph''' is a graph-theoretic structure in one of the systems of graphical syntax that Charles Sanders Peirce developed for logic. |
| + | |||
| + | In his papers on ''qualitative logic'', ''entitative graphs'', and ''existential graphs'', Peirce developed several versions of a graphical formalism, or a graph-theoretic formal language, designed to be interpreted for logic. | ||
In the century since Peirce initiated this line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph-theoretic structures. This article examines the common basis of these formal systems from a bird's eye view, focusing on those aspects of form that are shared by the entire family of algebras, calculi, or languages, however they happen to be viewed in a given application. | In the century since Peirce initiated this line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph-theoretic structures. This article examines the common basis of these formal systems from a bird's eye view, focusing on those aspects of form that are shared by the entire family of algebras, calculi, or languages, however they happen to be viewed in a given application. | ||
| Line 7: | Line 9: | ||
==Abstract point of view== | ==Abstract point of view== | ||
| − | + | {| width="100%" cellpadding="2" cellspacing="0" | |
| − | + | | width="60%" | | |
| + | | width="40%" | ''Wollust ward dem Wurm gegeben …'' | ||
| + | |- | ||
| + | | | ||
| + | | align="right" | — Friedrich Schiller, ''An die Freude'' | ||
| + | |} | ||
| − | The bird's eye view in question is more formally known as the perspective of formal equivalence, from which remove one cannot see many distinctions that appear momentous from lower levels of abstraction. In particular, expressions of different formalisms whose syntactic structures are | + | The bird's eye view in question is more formally known as the perspective of formal equivalence, from which remove one cannot see many distinctions that appear momentous from lower levels of abstraction. In particular, expressions of different formalisms whose syntactic structures are isomorphic from the standpoint of algebra or topology are not recognized as being different from each other in any significant sense. Though we may note in passing such historical details as the circumstance that Charles Sanders Peirce used a ''streamer-cross symbol'' where George Spencer Brown used a ''carpenter's square marker'', the theme of principal interest at the abstract level of form is neutral with regard to variations of that order. |
==In lieu of a beginning== | ==In lieu of a beginning== | ||
| − | + | Consider the formal equations indicated in Figures 1 and 2. | |
| − | + | {| align="center" border="0" cellpadding="10" cellspacing="0" | |
| + | | [[Image:Logical_Graph_Figure_1_Visible_Frame.jpg|500px]] || (1) | ||
| + | |- | ||
| + | | [[Image:Logical_Graph_Figure_2_Visible_Frame.jpg|500px]] || (2) | ||
| + | |} | ||
| − | + | For the time being these two forms of transformation may be referred to as ''axioms'' or ''initial equations''. | |
| − | |||
| − | |||
==Duality : logical and topological== | ==Duality : logical and topological== | ||
| − | There are two types of | + | There are two types of duality that have to be kept separately mind in the use of logical graphs — logical duality and topological duality. |
| − | There is a standard way that graphs of the order that Peirce considered, those embedded in a continuous | + | There is a standard way that graphs of the order that Peirce considered, those embedded in a continuous manifold like that commonly represented by a plane sheet of paper — with or without the paper bridges that Peirce used to augment its topological genus — can be represented in linear text as what are called ''parse strings'' or ''traversal strings'' and parsed into ''pointer structures'' in computer memory. |
A blank sheet of paper can be represented in linear text as a blank space, but that way of doing it tends to be confusing unless the logical expression under consideration is set off in a separate display. | A blank sheet of paper can be represented in linear text as a blank space, but that way of doing it tends to be confusing unless the logical expression under consideration is set off in a separate display. | ||
| Line 32: | Line 41: | ||
For example, consider the axiom or initial equation that is shown below: | For example, consider the axiom or initial equation that is shown below: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_3_Visible_Frame.jpg|500px]] || (3) | ||
| + | |} | ||
| − | This can be written inline as | + | This can be written inline as <math>{}^{\backprime\backprime} \texttt{( ( ) )} = \quad {}^{\prime\prime}\!</math> or set off in a text display as follows: |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | width="33%" | <math>\texttt{( ( ) )}\!</math> | |
| − | + | | width="34%" | <math>=\!</math> | |
| + | | width="33%" | | ||
| + | |} | ||
| − | When we turn to representing the corresponding expressions in computer memory, where they can be manipulated with utmost facility, we begin by transforming the planar graphs into their | + | When we turn to representing the corresponding expressions in computer memory, where they can be manipulated with utmost facility, we begin by transforming the planar graphs into their topological duals. The planar regions of the original graph correspond to nodes (or points) of the dual graph, and the boundaries between planar regions in the original graph correspond to edges (or lines) between the nodes of the dual graph. |
| − | For example, overlaying the corresponding | + | For example, overlaying the corresponding dual graphs on the plane-embedded graphs shown above, we get the following composite picture: |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_4_Visible_Frame.jpg|500px]] || (4) | ||
| + | |} | ||
| − | Though it's not really there in the most abstract topology of the matter, for all sorts of pragmatic reasons we find ourselves compelled to single out the outermost region of the plane in a distinctive way and to mark it as the '' | + | Though it's not really there in the most abstract topology of the matter, for all sorts of pragmatic reasons we find ourselves compelled to single out the outermost region of the plane in a distinctive way and to mark it as the ''root node'' of the corresponding dual graph. In the present style of Figure the root nodes are marked by horizontal strike-throughs. |
Extracting the dual graphs from their composite matrices, we get this picture: | Extracting the dual graphs from their composite matrices, we get this picture: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_5_Visible_Frame.jpg|500px]] || (5) | ||
| + | |} | ||
| − | It is easy to see the relationship between the parenthetical expressions of Peirce's logical graphs, that somewhat clippedly picture the ordered containments of their formal contents, and the associated | + | It is easy to see the relationship between the parenthetical expressions of Peirce's logical graphs, that somewhat clippedly picture the ordered containments of their formal contents, and the associated dual graphs, that constitute the species of rooted trees here to be described. |
| − | In the case of our last example, a moment's contemplation of the following picture will lead us to see that we can get the corresponding parenthesis string by starting at the root of the tree, climbing up the left side of the tree until we reach the top, then climbing back down the right side of the tree until we return to the root, all the while reading off the symbols, in this case either | + | In the case of our last example, a moment's contemplation of the following picture will lead us to see that we can get the corresponding parenthesis string by starting at the root of the tree, climbing up the left side of the tree until we reach the top, then climbing back down the right side of the tree until we return to the root, all the while reading off the symbols, in this case either <math>{}^{\backprime\backprime} \texttt{(} {}^{\prime\prime}\!</math> or <math>{}^{\backprime\backprime} \texttt{)} {}^{\prime\prime},\!</math> that we happen to encounter in our travels. |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_6_Visible_Frame.jpg|500px]] || (6) | ||
| + | |} | ||
| − | This ritual is called '' | + | This ritual is called ''traversing'' the tree, and the string read off is called the ''traversal string'' of the tree. The reverse ritual, that passes from the string to the tree, is called ''parsing'' the string, and the tree constructed is called the ''parse graph'' of the string. The speakers thereof tend to be a bit loose in this language, often using ''parse string'' to mean the string that gets parsed into the associated graph. |
| − | We have | + | We have treated in some detail various forms of the initial equation or logical axiom that is formulated in string form as <math>{}^{\backprime\backprime} \texttt{( ( ) )} = \quad {}^{\prime\prime}.~\!</math> For the sake of comparison, let's record the plane-embedded and topological dual forms of the axiom that is formulated in string form as <math>{}^{\backprime\backprime} \texttt{( )( )} = \texttt{( )} {}^{\prime\prime}.\!</math> |
First the plane-embedded maps: | First the plane-embedded maps: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_7_Visible_Frame.jpg|500px]] || (7) | ||
| + | |} | ||
| − | Next the plane maps and their dual trees superimposed: | + | Next the plane-embedded maps and their dual trees superimposed: |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_8_Visible_Frame.jpg|500px]] || (8) | ||
| + | |} | ||
Finally the dual trees by themselves: | Finally the dual trees by themselves: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_9_Visible_Frame.jpg|500px]] || (9) | ||
| + | |} | ||
And here are the parse trees with their traversal strings indicated: | And here are the parse trees with their traversal strings indicated: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_10_Visible_Frame.jpg|500px]] || (10) | ||
| + | |} | ||
| − | We have at this point enough material to begin thinking about the forms of | + | We have at this point enough material to begin thinking about the forms of analogy, iconicity, metaphor, morphism, whatever you want to call them, that are pertinent to the use of logical graphs in their various logical interpretations, for instance, those that Peirce described as ''entitative graphs'' and ''existential graphs''. |
==Computational representation== | ==Computational representation== | ||
| Line 86: | Line 113: | ||
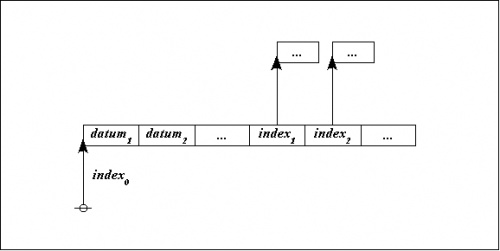
Nodes in a graph represent ''records'' in computer memory. A record is a collection of data that can be conceived to reside at a specific ''address''. The address of a record is analogous to a demonstrative pronoun, on which account programmers commonly describe it as a ''pointer'' and semioticians recognize it as a type of sign called an ''index''. | Nodes in a graph represent ''records'' in computer memory. A record is a collection of data that can be conceived to reside at a specific ''address''. The address of a record is analogous to a demonstrative pronoun, on which account programmers commonly describe it as a ''pointer'' and semioticians recognize it as a type of sign called an ''index''. | ||
| − | At the next level of concreteness, a pointer | + | At the next level of concreteness, a pointer-record structure is represented as follows: |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_11_Visible_Frame.jpg|500px]] || (11) | ||
| + | |} | ||
| − | This portrays <math> | + | This portrays the pointer <math>\mathit{index}_0\!</math> as the address of a record that contains the following data: |
| − | + | {| align="center" cellpadding="10" | |
| + | | <math>\mathit{datum}_1, \mathit{datum}_2, \mathit{datum}_3, \ldots,\!</math> and so on. | ||
| + | |} | ||
What makes it possible to represent graph-theoretical structures as data structures in computer memory is the fact that an address is just another datum, and so we may have a state of affairs like the following: | What makes it possible to represent graph-theoretical structures as data structures in computer memory is the fact that an address is just another datum, and so we may have a state of affairs like the following: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_12_Visible_Frame.jpg|500px]] || (12) | ||
| + | |} | ||
Returning to the abstract level, it takes three nodes to represent the three data records illustrated above: one root node connected to a couple of adjacent nodes. The items of data that do not point any further up the tree are then treated as labels on the record-nodes where they reside, as shown below: | Returning to the abstract level, it takes three nodes to represent the three data records illustrated above: one root node connected to a couple of adjacent nodes. The items of data that do not point any further up the tree are then treated as labels on the record-nodes where they reside, as shown below: | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_13_Visible_Frame.jpg|500px]] || (13) | ||
| + | |} | ||
Notice that drawing the arrows is optional with rooted trees like these, since singling out a unique node as the root induces a unique orientation on all the edges of the tree, with ''up'' being the same direction as ''away from the root''. | Notice that drawing the arrows is optional with rooted trees like these, since singling out a unique node as the root induces a unique orientation on all the edges of the tree, with ''up'' being the same direction as ''away from the root''. | ||
| Line 110: | Line 145: | ||
===Primary arithmetic as semiotic system=== | ===Primary arithmetic as semiotic system=== | ||
| − | Though it may not seem too exciting, logically speaking, there are many | + | Though it may not seem too exciting, logically speaking, there are many reasons to make oneself at home with the system of forms that is represented indifferently, topologically speaking, by rooted trees, balanced strings of parentheses, or finite sets of non-intersecting simple closed curves in the plane. |
| − | :* One reason is that it gives us a respectable example of a sign domain to cut our semiotic teeth | + | :* One reason is that it gives us a respectable example of a sign domain on which to cut our semiotic teeth, non-trivial in the sense that it contains a countable infinity of signs. |
| − | |||
| − | + | :* Another reason is that it allows us to study a simple form of computation that is recognizable as a species of ''[[semiosis]]'', or sign-transforming process. | |
| − | + | This space of forms, along with the two axioms that induce its partition into exactly two equivalence classes, is what George Spencer Brown called the ''primary arithmetic''. | |
| − | + | The axioms of the primary arithmetic are shown below, as they appear in both graph and string forms, along with pairs of names that come in handy for referring to the two opposing directions of applying the axioms. | |
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:Logical_Graph_Figure_14_Banner.jpg|500px]] || (14) | ||
| + | |- | ||
| + | | [[Image:Logical_Graph_Figure_15_Banner.jpg|500px]] || (15) | ||
| + | |} | ||
| + | |||
| + | Let <math>S\!</math> be the set of rooted trees and let <math>S_0\!</math> be the 2-element subset of <math>S\!</math> that consists of a rooted node and a rooted edge. | ||
| + | |||
| + | {| align="center" cellpadding="10" style="text-align:center" | ||
| + | | <math>S\!</math> | ||
| + | | <math>=\!</math> | ||
| + | | <math>\{ \text{rooted trees} \}\!</math> | ||
| + | |- | ||
| + | | <math>S_0\!</math> | ||
| + | | <math>=\!</math> | ||
| + | | <math>\{ \ominus, \vert \} = \{\!</math>[[Image:Rooted Node.jpg|16px]], [[Image:Rooted Edge.jpg|12px]]<math>\}\!</math> | ||
| + | |} | ||
| + | |||
| + | Simple intuition, or a simple inductive proof, assures us that any rooted tree can be reduced by way of the arithmetic initials either to a root node [[Image:Rooted Node.jpg|16px]] or else to a rooted edge [[Image:Rooted Edge.jpg|12px]] . | ||
For example, consider the reduction that proceeds as follows: | For example, consider the reduction that proceeds as follows: | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Logical_Graph_Figure_16.jpg|500px]] || (16) | |
| − | | | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Regarded as a semiotic process, this amounts to a sequence of signs, every one after the first | + | Regarded as a semiotic process, this amounts to a sequence of signs, every one after the first serving as the ''interpretant'' of its predecessor, ending in a final sign that may be taken as the canonical sign for their common object, in the upshot being the result of the computation process. Simple as it is, this exhibits the main features of any computation, namely, a semiotic process that proceeds from an obscure sign to a clear sign of the same object, being in its aim and effect an action on behalf of clarification. |
===Primary algebra as pattern calculus=== | ===Primary algebra as pattern calculus=== | ||
| − | Experience teaches that complex objects are best approached in a gradual, laminar, | + | Experience teaches that complex objects are best approached in a gradual, laminar, modular fashion, one step, one layer, one piece at a time, and it's just as much the case when the complexity of the object is irreducible, that is, when the articulations of the representation are necessarily at joints that are cloven disjointedly from nature, with some assembly required in the synthetic integrity of the intuition. |
That's one good reason for spending so much time on the first half of [[zeroth order logic]], represented here by the primary arithmetic, a level of formal structure that C.S. Peirce verged on intuiting at numerous points and times in his work on logical graphs, and that Spencer Brown named and brought more completely to life. | That's one good reason for spending so much time on the first half of [[zeroth order logic]], represented here by the primary arithmetic, a level of formal structure that C.S. Peirce verged on intuiting at numerous points and times in his work on logical graphs, and that Spencer Brown named and brought more completely to life. | ||
| − | There is one other reason for lingering a while longer in these primitive forests, and this is that an acquaintance with | + | There is one other reason for lingering a while longer in these primitive forests, and this is that an acquaintance with “bare trees”, those as yet unadorned with literal or numerical labels, will provide a firm basis for understanding what's really at issue in such problems as the “ontological status of variables”. |
| − | |||
| − | |||
| − | + | It is probably best to illustrate this theme in the setting of a concrete case, which we can do by reviewing the previous example of reductive evaluation shown in Figure 16. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The observation of several semioses of roughly this shape will most | + | The observation of several ''semioses'', or sign-transformations, of roughly this shape will most likely lead an observer with any observational facility whatever to notice that it doesn't really matter what sorts of branches happen to sprout from the side of the root aside from the lone edge that also grows there — the end result will always be the same. |
Our observer might think to summarize the results of many such observations by introducing a label or variable to signify any shape of branch whatever, writing something like the following: | Our observer might think to summarize the results of many such observations by introducing a label or variable to signify any shape of branch whatever, writing something like the following: | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Logical_Graph_Figure_17.jpg|500px]] || (17) | |
| − | + | |} | |
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
Observations like that, made about an arithmetic of any variety, germinated by their summarizations, are the root of all algebra. | Observations like that, made about an arithmetic of any variety, germinated by their summarizations, are the root of all algebra. | ||
| − | Speaking of algebra, and having encountered already one example of an algebraic law, we might as well introduce the axioms of the ''primary algebra'', once again deriving their substance and their name from the works of | + | Speaking of algebra, and having encountered already one example of an algebraic law, we might as well introduce the axioms of the ''primary algebra'', once again deriving their substance and their name from the works of Charles Sanders Peirce and George Spencer Brown, respectively. |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Logical_Graph_Figure_18.jpg|500px]] || (18) | |
| − | | | + | |- |
| − | + | | [[Image:Logical_Graph_Figure_19.jpg|500px]] || (19) | |
| − | + | |} | |
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | + | The choice of axioms for any formal system is to some degree a matter of aesthetics, as it is commonly the case that many different selections of formal rules will serve as axioms to derive all the rest as theorems. As it happens, the example of an algebraic law that we noticed first, <math>a \texttt{( )} = \texttt{( )},~\!</math> as simple as it appears, proves to be provable as a theorem on the grounds of the foregoing axioms. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The choice of axioms for any formal system is to some degree a matter of aesthetics, as it is commonly the case that many different selections of formal rules will serve as axioms to derive all the rest as theorems. As it happens, the example of an algebraic law that we noticed first, | ||
We might also notice at this point a subtle difference between the primary arithmetic and the primary algebra with respect to the grounds of justification that we have naturally if tacitly adopted for their respective sets of axioms. | We might also notice at this point a subtle difference between the primary arithmetic and the primary algebra with respect to the grounds of justification that we have naturally if tacitly adopted for their respective sets of axioms. | ||
| − | The arithmetic axioms were introduced by fiat, in a | + | The arithmetic axioms were introduced by fiat, in an ''a priori'' fashion, though of course it is only long prior experience with the practical uses of comparably developed generations of formal systems that would actually induce us to such a quasi-primal move. The algebraic axioms, in contrast, can be seen to derive their motive and their justice from the observation and summarization of patterns that are visible in the arithmetic spectrum. |
==Formal development== | ==Formal development== | ||
| Line 276: | Line 221: | ||
What precedes this point is intended as an informal introduction to the axioms of the primary arithmetic and primary algebra, and hopefully provides the reader with an intuitive sense of their motivation and rationale. | What precedes this point is intended as an informal introduction to the axioms of the primary arithmetic and primary algebra, and hopefully provides the reader with an intuitive sense of their motivation and rationale. | ||
| − | The next order of business is to give the exact forms of the axioms that are used in the following more formal development, devolving from Peirce's various systems of logical graphs via Spencer-Brown's ''Laws of Form'' (LOF). In formal proofs, a variation of the annotation scheme from LOF will be used to mark each step of the proof according to which axiom, or 'initial', is being invoked to justify the corresponding step of syntactic transformation, whether it applies to graphs or to strings. | + | The next order of business is to give the exact forms of the axioms that are used in the following more formal development, devolving from Peirce's various systems of logical graphs via Spencer-Brown's ''Laws of Form'' (LOF). In formal proofs, a variation of the annotation scheme from LOF will be used to mark each step of the proof according to which axiom, or ''initial'', is being invoked to justify the corresponding step of syntactic transformation, whether it applies to graphs or to strings. |
===Axioms=== | ===Axioms=== | ||
| − | The axioms are just four in number, divided into the ''arithmetic initials'' | + | The axioms are just four in number, divided into the ''arithmetic initials'', <math>I_1\!</math> and <math>I_2,\!</math> and the ''algebraic initials'', <math>J_1\!</math> and <math>J_2.\!</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | {| align="center" cellpadding=" | + | {| align="center" cellpadding="10" |
| − | + | | [[Image:Logical_Graph_Figure_20.jpg|500px]] || (20) | |
| − | |||
| − | | | ||
| − | | | ||
|- | |- | ||
| − | | | + | | [[Image:Logical_Graph_Figure_21.jpg|500px]] || (21) |
| − | | | ||
| − | | | ||
| − | | | ||
|- | |- | ||
| − | | | + | | [[Image:Logical_Graph_Figure_22.jpg|500px]] || (22) |
| − | | | ||
| − | | | ||
| − | | | ||
|- | |- | ||
| − | | | + | | [[Image:Logical_Graph_Figure_23.jpg|500px]] || (23) |
| − | | | ||
| − | | | ||
| − | | | ||
|} | |} | ||
| − | + | One way of assigning logical meaning to the initial equations is known as the ''entitative interpretation'' (EN). Under EN, the axioms read as follows: | |
| − | {| align="center" cellpadding=" | + | {| align="center" cellpadding="10" |
| − | + | | | |
| − | | | + | <math>\begin{array}{ccccc} |
| − | | | + | I_1 & : & |
| − | + | \operatorname{true}\ \operatorname{or}\ \operatorname{true} & = & | |
| − | | | + | \operatorname{true} \\ |
| − | + | I_2 & : & | |
| − | + | \operatorname{not}\ \operatorname{true}\ & = & | |
| − | + | \operatorname{false} \\ | |
| − | + | J_1 & : & | |
| − | + | a\ \operatorname{or}\ \operatorname{not}\ a & = & | |
| − | + | \operatorname{true} \\ | |
| − | + | J_2 & : & | |
| − | + | (a\ \operatorname{or}\ b)\ \operatorname{and}\ (a\ \operatorname{or}\ c) & = & | |
| − | + | a\ \operatorname{or}\ (b\ \operatorname{and}\ c) \\ | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | + | ||
| − | + | Another way of assigning logical meaning to the initial equations is known as the ''existential interpretation'' (EX). Under EX, the axioms read as follows: | |
| − | + | ||
| + | {| align="center" cellpadding="10" | ||
| + | | | ||
| + | <math>\begin{array}{ccccc} | ||
| + | I_1 & : & | ||
| + | \operatorname{false}\ \operatorname{and}\ \operatorname{false} & = & | ||
| + | \operatorname{false} \\ | ||
| + | I_2 & : & | ||
| + | \operatorname{not}\ \operatorname{false} & = & | ||
| + | \operatorname{true} \\ | ||
| + | J_1 & : & | ||
| + | a\ \operatorname{and}\ \operatorname{not}\ a & = & | ||
| + | \operatorname{false} \\ | ||
| + | J_2 & : & | ||
| + | (a\ \operatorname{and}\ b)\ \operatorname{or}\ (a\ \operatorname{and}\ c) & = & | ||
| + | a\ \operatorname{and}\ (b\ \operatorname{or}\ c) \\ | ||
| + | \end{array}</math> | ||
|} | |} | ||
| − | All of the axioms in this set have the form of equations. This means that all of the inference steps that they allow are reversible. The proof annotation scheme employed below makes use of a double bar | + | All of the axioms in this set have the form of equations. This means that all of the inference steps that they allow are reversible. The proof annotation scheme employed below makes use of a double bar <math>=\!=\!=\!=\!=\!=</math> to mark this fact, although it will often be left to the reader to decide which of the two possible directions is the one required for applying the indicated axiom. |
===Frequently used theorems=== | ===Frequently used theorems=== | ||
| − | The actual business of proof is a far more strategic affair than the simple cranking of inference rules might suggest. Part of the reason for this lies in the circumstance that the usual brands of inference rules combine the moving forward of a state of inquiry with the losing of information along the way that doesn't appear to be immediately relevant, at least, not as viewed in the local focus and the short run of the moment to moment proceedings of the proof in question. Over the long haul, this has the pernicious side-effect that one is forever strategically required to reconstruct much of the information that one had strategically thought to forget in earlier stages of the proof, if | + | The actual business of proof is a far more strategic affair than the simple cranking of inference rules might suggest. Part of the reason for this lies in the circumstance that the usual brands of inference rules combine the moving forward of a state of inquiry with the losing of information along the way that doesn't appear to be immediately relevant, at least, not as viewed in the local focus and the short run of the moment to moment proceedings of the proof in question. Over the long haul, this has the pernicious side-effect that one is forever strategically required to reconstruct much of the information that one had strategically thought to forget in earlier stages of the proof, if "before the proof started" can be counted as an earlier stage of the proof in view. |
| − | + | For this reason, among others, it is very instructive to study equational inference rules of the sort that our axioms have just provided. Although equational forms of reasoning are paramount in mathematics, they are less familiar to the student of conventional logic textbooks, who may find a few surprises here. | |
By way of gaining a minimal experience with how equational proofs look in the present forms of syntax, let us examine the proofs of a few essential theorems in the primary algebra. | By way of gaining a minimal experience with how equational proofs look in the present forms of syntax, let us examine the proofs of a few essential theorems in the primary algebra. | ||
| − | ====C<sub>1</sub>. | + | ====C<sub>1</sub>. Double negation==== |
| − | The first theorem goes under the names of ''Consequence 1'' | + | The first theorem goes under the names of ''Consequence 1'' <math>(C_1)\!</math>, the ''double negation theorem'' (DNT), or ''Reflection''. |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Double Negation 1.0 Splash Page.png|500px]] || (24) | |
| − | | | + | |} |
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The proof that follows is adapted from the one that was given by | + | The proof that follows is adapted from the one that was given by George Spencer Brown in his book ''Laws of Form'' (LOF) and credited to two of his students, John Dawes and D.A. Utting. |
| − | + | {| align="center" cellpadding="8" | |
| − | + | | | |
| − | | | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" |
| − | + | |- | |
| − | | | + | | [[Image:Double Negation 1.0 Marquee Title.png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Double Negation 1.0 Storyboard 1.png|500px]] | |
| − | | | + | |- |
| − | + | | [[Image:Equational Inference I2 Elicit (( )).png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Double Negation 1.0 Storyboard 2.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Equational Inference J1 Insert (a).png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Double Negation 1.0 Storyboard 3.png|500px]] | |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference J2 Distribute ((a)).png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Double Negation 1.0 Storyboard 4.png|500px]] | |
| − | | | + | |- |
| − | + | | [[Image:Equational Inference J1 Delete (a).png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Double Negation 1.0 Storyboard 5.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Equational Inference J1 Insert a.png|500px]] | |
| − | | | + | |- |
| − | | | + | | [[Image:Double Negation 1.0 Storyboard 6.png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Equational Inference J2 Collect a.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Double Negation 1.0 Storyboard 7.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Equational Inference J1 Delete ((a)).png|500px]] | |
| − | + | |- | |
| − | | | + | | [[Image:Double Negation 1.0 Storyboard 8.png|500px]] |
| − | + | |- | |
| − | + | | [[Image:Equational Inference I2 Cancel (( )).png|500px]] | |
| − | + | |- | |
| − | | | + | | [[Image:Double Negation 1.0 Storyboard 9.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Marquee QED.png|500px]] |
| − | + | |} | |
| − | + | | (25) | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | + | The steps of this proof are replayed in the following animation. | |
| − | + | {| align="center" cellpadding="8" | |
| + | | | ||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" | ||
| + | |- | ||
| + | | [[Image:Double Negation 2.0 Animation.gif]] | ||
| + | |} | ||
| + | | (26) | ||
| + | |} | ||
| − | < | + | ====C<sub>2</sub>. Generation theorem==== |
| − | + | ||
| − | + | One theorem of frequent use goes under the nickname of the ''weed and seed theorem'' (WAST). The proof is just an exercise in mathematical induction, once a suitable basis is laid down, and it will be left as an exercise for the reader. What the WAST says is that a label can be freely distributed or freely erased anywhere in a subtree whose root is labeled with that label. The second in our list of frequently used theorems is in fact the base case of this weed and seed theorem. In LOF, it goes by the names of ''Consequence 2'' <math>(C_2)\!</math> or ''Generation''. | |
| − | + | ||
| − | | | + | {| align="center" cellpadding="10" |
| − | + | | [[Image:Generation Theorem 1.0 Splash Page.png|500px]] || (27) | |
| − | + | |} | |
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
Here is a proof of the Generation Theorem. | Here is a proof of the Generation Theorem. | ||
| − | + | {| align="center" cellpadding="8" | |
| − | + | | | |
| − | | | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" |
| − | + | |- | |
| − | | | + | | [[Image:Generation Theorem 1.0 Marquee Title.png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Generation Theorem 1.0 Storyboard 1.png|500px]] | |
| − | + | |- | |
| − | | | + | | [[Image:Equational Inference C1 Reflect a(b).png|500px]] |
| − | + | |- | |
| − | + | | [[Image:Generation Theorem 1.0 Storyboard 2.png|500px]] | |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference I2 Elicit (( )).png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Generation Theorem 1.0 Storyboard 3.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Equational Inference J1 Insert a.png|500px]] | |
| − | | | + | |- |
| − | + | | [[Image:Generation Theorem 1.0 Storyboard 4.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Equational Inference J2 Collect a.png|500px]] | |
| − | | | + | |- |
| − | | | + | | [[Image:Generation Theorem 1.0 Storyboard 5.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference C1 Reflect a, b.png|500px]] |
| − | + | |- | |
| − | + | | [[Image:Generation Theorem 1.0 Storyboard 6.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Equational Inference Marquee QED.png|500px]] | |
| − | + | |} | |
| − | + | | (28) | |
| − | | | + | |} |
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | + | The steps of this proof are replayed in the following animation. | |
| − | The third of the frequently used theorems of service to this survey is one that Spencer-Brown annotates as ''Consequence 3'' | + | {| align="center" cellpadding="8" |
| + | | | ||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" | ||
| + | |- | ||
| + | | [[Image:Generation Theorem 2.0 Animation.gif]] | ||
| + | |} | ||
| + | | (29) | ||
| + | |} | ||
| + | |||
| + | ====C<sub>3</sub>. Dominant form theorem==== | ||
| + | |||
| + | The third of the frequently used theorems of service to this survey is one that Spencer-Brown annotates as ''Consequence 3'' <math>(C_3)\!</math> or ''Integration''. A better mnemonic might be ''dominance and recession theorem'' (DART), but perhaps the brevity of ''dominant form theorem'' (DFT) is sufficient reminder of its double-edged role in proofs. | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Dominant Form 1.0 Splash Page.png|500px]] || (30) | |
| − | | | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
Here is a proof of the Dominant Form Theorem. | Here is a proof of the Dominant Form Theorem. | ||
| − | + | {| align="center" cellpadding="8" | |
| − | + | | | |
| − | | | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" |
| − | + | |- | |
| − | | | + | | [[Image:Dominant Form 1.0 Marquee Title.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Dominant Form 1.0 Storyboard 1.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference C2 Regenerate a.png|500px]] |
| − | + | |- | |
| − | | | + | | [[Image:Dominant Form 1.0 Storyboard 2.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference J1 Delete a.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Dominant Form 1.0 Storyboard 3.png|500px]] |
| − | + | |- | |
| − | | | + | | [[Image:Equational Inference Marquee QED.png|500px]] |
| − | | | + | |} |
| − | | | + | | (31) |
| − | | | + | |} |
| − | | | + | |
| − | + | The following animation provides an instant re*play. | |
| − | + | ||
| + | {| align="center" cellpadding="8" | ||
| + | | | ||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" | ||
| + | |- | ||
| + | | [[Image:Dominant Form 2.0 Animation.gif]] | ||
| + | |} | ||
| + | | (32) | ||
| + | |} | ||
===Exemplary proofs=== | ===Exemplary proofs=== | ||
| − | + | Based on the axioms given at the outest, and aided by the theorems recorded so far, it is possible to prove a multitude of much more complex theorems. A couple of all-time favorites are given next. | |
====Peirce's law==== | ====Peirce's law==== | ||
| − | ''[[Peirce's law | + | : ''Main article'' : [[Peirce's law]] |
| + | |||
| + | Peirce's law is commonly written in the following form: | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | <math>((p \Rightarrow q) \Rightarrow p) \Rightarrow p\!</math> | |
| + | |} | ||
| − | The | + | The existential graph representation of Peirce's law is shown in Figure 33. |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Peirce's Law 1.0 Splash Page.png|500px]] || (33) | |
| − | | Peirce's Law | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | + | A graphical proof of Peirce's law is shown in Figure 34. | |
| − | + | {| align="center" cellpadding="8" | |
| − | + | | | |
| − | | Peirce's Law. | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" |
| − | + | |- | |
| − | | | + | | [[Image:Peirce's Law 1.0 Marquee Title.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Peirce's Law 1.0 Storyboard 1.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Band Collect p.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Peirce's Law 1.0 Storyboard 2.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Band Quit ((q)).png|500px]] |
| − | + | |- | |
| − | | | + | | [[Image:Peirce's Law 1.0 Storyboard 3.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Band Cancel (( )).png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Peirce's Law 1.0 Storyboard 4.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Band Delete p.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Peirce's Law 1.0 Storyboard 5.png|500px]] |
| − | + | |- | |
| − | + | | [[Image:Equational Inference Band Cancel (( )).png|500px]] | |
| − | + | |- | |
| − | | | + | | [[Image:Peirce's Law 1.0 Storyboard 6.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Marquee QED.png|500px]] |
| − | | | + | |} |
| − | | | + | | (34) |
| − | + | |} | |
| − | + | ||
| − | + | The following animation replays the steps of the proof. | |
| − | | | + | |
| − | + | {| align="center" cellpadding="8" | |
| − | | | + | | |
| − | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" | |
| − | + | |- | |
| − | + | | [[Image:Peirce's Law 2.0 Animation.gif]] | |
| − | | | + | |} |
| − | | | + | | (35) |
| − | | | + | |} |
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
====Praeclarum theorema==== | ====Praeclarum theorema==== | ||
| − | An illustrious example of a propositional theorem is the ''praeclarum theorema'', the ''admirable'', ''shining'', or ''splendid'' theorem of | + | An illustrious example of a propositional theorem is the ''praeclarum theorema'', the ''admirable'', ''shining'', or ''splendid'' theorem of Leibniz. |
| + | |||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| + | | | ||
| + | <p>If ''a'' is ''b'' and ''d'' is ''c'', then ''ad'' will be ''bc''.</p> | ||
| + | |||
| + | <p>This is a fine theorem, which is proved in this way:</p> | ||
| + | |||
| + | <p>''a'' is ''b'', therefore ''ad'' is ''bd'' (by what precedes),</p> | ||
| + | |||
| + | <p>''d'' is ''c'', therefore ''bd'' is ''bc'' (again by what precedes),</p> | ||
| + | |||
| + | <p>''ad'' is ''bd'', and ''bd'' is ''bc'', therefore ''ad'' is ''bc''. Q.E.D.</p> | ||
| − | + | <p>(Leibniz, ''Logical Papers'', p. 41).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
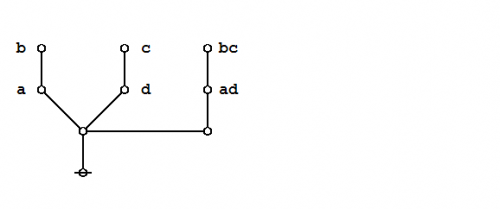
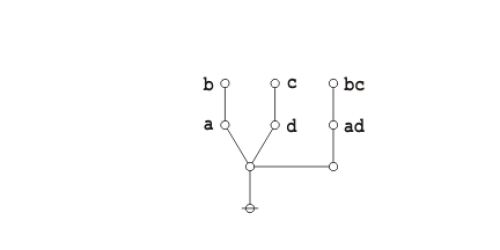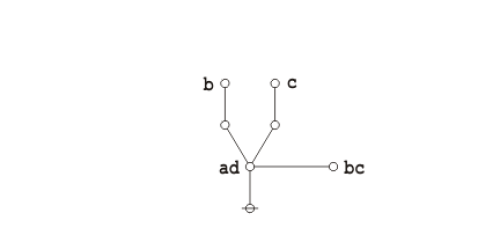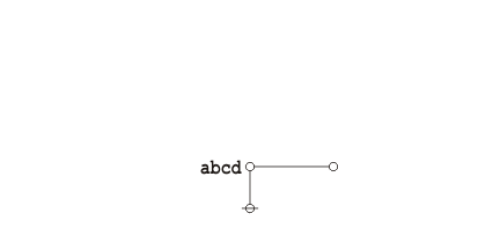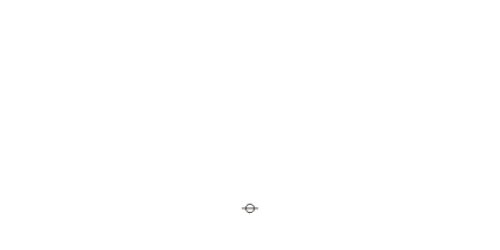
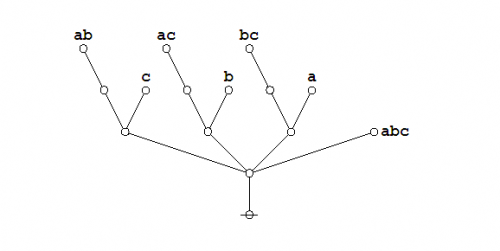
Under the existential interpretation, the praeclarum theorema is represented by means of the following logical graph. | Under the existential interpretation, the praeclarum theorema is represented by means of the following logical graph. | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Praeclarum Theorema 1.0 Splash Page.png|500px]] || (36) | |
| − | | Praeclarum Theorema | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
And here's a neat proof of that nice theorem. | And here's a neat proof of that nice theorem. | ||
| − | + | {| align="center" cellpadding="8" | |
| − | + | | | |
| − | | Praeclarum Theorema | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" |
| − | + | |- | |
| − | | | + | | [[Image:Praeclarum Theorema 1.0 Marquee Title.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 1.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Rule Reflect ad(bc).png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 2.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Rule Weed a, d.png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 3.png|500px]] | |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Rule Reflect b, c.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 4.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Rule Weed bc.png|500px]] |
| − | | | + | |- |
| − | | | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 5.png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Equational Inference Rule Quit abcd.png|500px]] | |
| − | + | |- | |
| − | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 6.png|500px]] | |
| − | + | |- | |
| − | | | + | | [[Image:Equational Inference Rule Cancel (( )).png|500px]] |
| − | | | + | |- |
| − | + | | [[Image:Praeclarum Theorema 1.0 Storyboard 7.png|500px]] | |
| − | | | + | |- |
| − | | | + | | [[Image:Equational Inference Marquee QED.png|500px]] |
| − | | | + | |} |
| − | | | + | | (37) |
| − | | | + | |} |
| − | + | ||
| − | | | + | The steps of the proof are replayed in the following animation. |
| − | | | + | |
| − | | | + | {| align="center" cellpadding="8" |
| − | | | + | | |
| − | | | + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" |
| − | | | + | |- |
| − | + | | [[Image:Praeclarum Theorema 2.0 Animation.gif]] | |
| − | | | + | |} |
| − | | | + | | (38) |
| − | | | + | |} |
| − | | | + | |
| − | | | + | ====Two-thirds majority function==== |
| − | | | + | |
| − | + | Consider the following equation in boolean algebra, posted as a [http://mathoverflow.net/questions/9292/newbie-boolean-algebra-question problem for proof] at [http://mathoverflow.net/ MathOverFlow]. | |
| − | | | + | |
| − | | | + | {| align="center" cellpadding="20" |
| − | | | + | | |
| − | | | + | <math>\begin{matrix} |
| − | | | + | a b \bar{c} + a \bar{b} c + \bar{a} b c + a b c |
| − | | | + | \\[6pt] |
| − | + | \iff | |
| − | | | + | \\[6pt] |
| − | | | + | a b + a c + b c |
| − | | | + | \end{matrix}</math> |
| − | + | | | |
| − | + | |} | |
| + | |||
| + | The required equation can be proven in the medium of logical graphs as shown in the following Figure. | ||
| + | |||
| + | {| align="center" cellpadding="8" | ||
| + | | | ||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority Eq 1 Pf 1 Banner Title.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 1.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Reflect ab, ac, bc.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 2.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Distribute (abc).png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 3.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Collect ab, ac, bc.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 4.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Quit (a), (b), (c).png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 5.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Cancel (( )).png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 6.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Weed ab, ac, bc.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 7.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Delete a, b, c.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 8.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Bar Cancel (( )).png|500px]] | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority 2.0 Eq 1 Pf 1 Storyboard 9.png|500px]] | ||
| + | |- | ||
| + | | [[Image:Equational Inference Banner QED.png|500px]] | ||
| + | |} | ||
| + | | (39) | ||
| + | |} | ||
| + | |||
| + | Here's an animated recap of the graphical transformations that occur in the above proof: | ||
| + | |||
| + | {| align="center" cellpadding="8" | ||
| + | | | ||
| + | {| align="center" cellpadding="0" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center" | ||
| + | |- | ||
| + | | [[Image:Two-Thirds Majority Function 500 x 250 Animation.gif]] | ||
| + | |} | ||
| + | | (40) | ||
| + | |} | ||
==Bibliography== | ==Bibliography== | ||
| − | * | + | * Leibniz, G.W. (1679–1686 ?), “Addenda to the Specimen of the Universal Calculus”, pp. 40–46 in G.H.R. Parkinson (ed. and trans., 1966), ''Leibniz : Logical Papers'', Oxford University Press, London, UK. |
| + | |||
| + | * Peirce, C.S. (1931–1935, 1958), ''Collected Papers of Charles Sanders Peirce'', vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA. Cited as (CP volume.paragraph). | ||
| + | |||
| + | * Peirce, C.S. (1981–), ''Writings of Charles S. Peirce : A Chronological Edition'', Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN. Cited as (CE volume, page). | ||
| + | |||
| + | * Peirce, C.S. (1885), “On the Algebra of Logic : A Contribution to the Philosophy of Notation”, ''American Journal of Mathematics'' 7 (1885), 180–202. Reprinted as CP 3.359–403 and CE 5, 162–190. | ||
| + | |||
| + | * Peirce, C.S. (''c.'' 1886), “Qualitative Logic”, MS 736. Published as pp. 101–115 in Carolyn Eisele (ed., 1976), ''The New Elements of Mathematics by Charles S. Peirce, Volume 4, Mathematical Philosophy'', Mouton, The Hague. | ||
| + | |||
| + | * Peirce, C.S. (1886 a), “Qualitative Logic”, MS 582. Published as pp. 323–371 in ''Writings of Charles S. Peirce : A Chronological Edition, Volume 5, 1884–1886'', Peirce Edition Project (eds.), Indiana University Press, Bloomington, IN, 1993. | ||
| + | |||
| + | * Peirce, C.S. (1886 b), “The Logic of Relatives : Qualitative and Quantitative”, MS 584. Published as pp. 372–378 in ''Writings of Charles S. Peirce : A Chronological Edition, Volume 5, 1884–1886'', Peirce Edition Project (eds.), Indiana University Press, Bloomington, IN, 1993. | ||
| + | |||
| + | * Spencer Brown, George (1969), ''Laws of Form'', George Allen and Unwin, London, UK. | ||
| + | |||
| + | ==Resources== | ||
| + | |||
| + | * [http://planetmath.org/ PlanetMath] | ||
| + | ** [http://planetmath.org/LogicalGraphIntroduction Logical Graph : Introduction] | ||
| + | ** [http://planetmath.org/LogicalGraphFormalDevelopment Logical Graph : Formal Development] | ||
| + | |||
| + | * Bergman and Paavola (eds.), [http://www.helsinki.fi/science/commens/dictionary.html Commens Dictionary of Peirce's Terms] | ||
| + | ** [http://www.helsinki.fi/science/commens/terms/graphexis.html Existential Graph] | ||
| + | ** [http://www.helsinki.fi/science/commens/terms/graphlogi.html Logical Graph] | ||
| + | |||
| + | * [http://dr-dau.net/index.shtml Dau, Frithjof] | ||
| + | ** [http://dr-dau.net/eg_readings.shtml Peirce's Existential Graphs : Readings and Links] | ||
| + | ** [http://web.archive.org/web/20070706192257/http://dr-dau.net/pc.shtml Existential Graphs as Moving Pictures of Thought] — Computer Animated Proof of Leibniz's Praeclarum Theorema | ||
| + | |||
| + | * [http://www.math.uic.edu/~kauffman/ Kauffman, Louis H.] | ||
| + | ** [http://www.math.uic.edu/~kauffman/Arithmetic.htm Box Algebra, Boundary Mathematics, Logic, and Laws of Form] | ||
| − | * [[ | + | * [http://mathworld.wolfram.com/ MathWorld : A Wolfram Web Resource] |
| + | ** [http://mathworld.wolfram.com/about/author.html Weisstein, Eric W.], [http://mathworld.wolfram.com/Spencer-BrownForm.html Spencer-Brown Form] | ||
| − | * [ | + | * Shoup, Richard (ed.), [http://www.lawsofform.org/ Laws of Form Web Site] |
| + | ** Spencer-Brown, George (1973), [http://www.lawsofform.org/aum/session1.html Transcript Session One], [http://www.lawsofform.org/aum/ AUM Conference], Esalen, CA. | ||
| − | + | ==Translations== | |
| − | * | + | * [http://pt.wikipedia.org/wiki/Grafo_l%C3%B3gico Grafo lógico], [http://pt.wikipedia.org/ Portuguese Wikipedia]. |
| − | + | ==Syllabus== | |
| − | + | ===Focal nodes=== | |
| − | * | + | * [[Inquiry Live]] |
| + | * [[Logic Live]] | ||
| − | + | ===Peer nodes=== | |
| − | + | * [http://intersci.ss.uci.edu/wiki/index.php/Logical_graph Logical Graph @ InterSciWiki] | |
| + | * [http://mywikibiz.com/Logical_graph Logical Graph @ MyWikiBiz] | ||
| + | * [http://ref.subwiki.org/wiki/Logical_graph Logical Graph @ Subject Wikis] | ||
| + | * [http://en.wikiversity.org/wiki/Logical_graph Logical Graph @ Wikiversity] | ||
| + | * [http://beta.wikiversity.org/wiki/Logical_graph Logical Graph @ Wikiversity Beta] | ||
| − | === | + | ===Logical operators=== |
| − | * [[ | + | {{col-begin}} |
| + | {{col-break}} | ||
| + | * [[Exclusive disjunction]] | ||
| + | * [[Logical conjunction]] | ||
| + | * [[Logical disjunction]] | ||
| + | * [[Logical equality]] | ||
| + | {{col-break}} | ||
| + | * [[Logical implication]] | ||
| + | * [[Logical NAND]] | ||
| + | * [[Logical NNOR]] | ||
| + | * [[Logical negation|Negation]] | ||
| + | {{col-end}} | ||
===Related topics=== | ===Related topics=== | ||
| − | { | + | |
| − | + | {{col-begin}} | |
| + | {{col-break}} | ||
* [[Ampheck]] | * [[Ampheck]] | ||
| − | |||
* [[Boolean domain]] | * [[Boolean domain]] | ||
* [[Boolean function]] | * [[Boolean function]] | ||
| − | |||
* [[Boolean-valued function]] | * [[Boolean-valued function]] | ||
| − | + | * [[Differential logic]] | |
| − | * [[ | + | {{col-break}} |
| − | + | * [[Logical graph]] | |
| − | * [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* [[Minimal negation operator]] | * [[Minimal negation operator]] | ||
| + | * [[Multigrade operator]] | ||
| + | * [[Parametric operator]] | ||
* [[Peirce's law]] | * [[Peirce's law]] | ||
| + | {{col-break}} | ||
* [[Propositional calculus]] | * [[Propositional calculus]] | ||
| + | * [[Sole sufficient operator]] | ||
* [[Truth table]] | * [[Truth table]] | ||
| + | * [[Universe of discourse]] | ||
* [[Zeroth order logic]] | * [[Zeroth order logic]] | ||
| − | |} | + | {{col-end}} |
| + | |||
| + | ===Relational concepts=== | ||
| + | |||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
| + | * [[Continuous predicate]] | ||
| + | * [[Hypostatic abstraction]] | ||
| + | * [[Logic of relatives]] | ||
| + | * [[Logical matrix]] | ||
| + | {{col-break}} | ||
| + | * [[Relation (mathematics)|Relation]] | ||
| + | * [[Relation composition]] | ||
| + | * [[Relation construction]] | ||
| + | * [[Relation reduction]] | ||
| + | {{col-break}} | ||
| + | * [[Relation theory]] | ||
| + | * [[Relative term]] | ||
| + | * [[Sign relation]] | ||
| + | * [[Triadic relation]] | ||
| + | {{col-end}} | ||
| + | |||
| + | ===Information, Inquiry=== | ||
| + | |||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
| + | * [[Inquiry]] | ||
| + | * [[Dynamics of inquiry]] | ||
| + | {{col-break}} | ||
| + | * [[Semeiotic]] | ||
| + | * [[Logic of information]] | ||
| + | {{col-break}} | ||
| + | * [[Descriptive science]] | ||
| + | * [[Normative science]] | ||
| + | {{col-break}} | ||
| + | * [[Pragmatic maxim]] | ||
| + | * [[Truth theory]] | ||
| + | {{col-end}} | ||
| + | |||
| + | ===Related articles=== | ||
| + | |||
| + | {{col-begin}} | ||
| + | {{col-break}} | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Cactus_Language Cactus Language] | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Futures_Of_Logical_Graphs Futures Of Logical Graphs] | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Propositional_Equation_Reasoning_Systems Propositional Equation Reasoning Systems] | ||
| + | {{col-break}} | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_:_Introduction Differential Logic : Introduction] | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Differential_Propositional_Calculus Differential Propositional Calculus] | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_and_Dynamic_Systems_2.0 Differential Logic and Dynamic Systems] | ||
| + | {{col-break}} | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Prospects_for_Inquiry_Driven_Systems Prospects for Inquiry Driven Systems] | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Introduction_to_Inquiry_Driven_Systems Introduction to Inquiry Driven Systems] | ||
| + | * [http://intersci.ss.uci.edu/wiki/index.php/Inquiry_Driven_Systems Inquiry Driven Systems : Inquiry Into Inquiry] | ||
| + | {{col-end}} | ||
| − | == | + | ==Document history== |
| − | + | Portions of the above article were adapted from the following sources under the [[GNU Free Documentation License]], under other applicable licenses, or by permission of the copyright holders. | |
| − | |||
| − | |||
| − | + | * [http://intersci.ss.uci.edu/wiki/index.php/Logical_graph Logical Graph], [http://intersci.ss.uci.edu/ InterSciWiki] | |
| + | * [http://mywikibiz.com/Logical_graph Logical Graph], [http://mywikibiz.com/ MyWikiBiz] | ||
| + | * [http://planetmath.org/LogicalGraphIntroduction Logical Graph 1], [http://planetmath.org/ PlanetMath] | ||
| + | * [http://planetmath.org/LogicalGraphFormalDevelopment Logical Graph 2], [http://planetmath.org/ PlanetMath] | ||
| + | * [http://semanticweb.org/wiki/Logical_graph Logical Graph], [http://semanticweb.org/ Semantic Web] | ||
| + | * [http://wikinfo.org/w/index.php/Logical_graph Logical Graph], [http://wikinfo.org/w/ Wikinfo] | ||
| + | * [http://en.wikiversity.org/wiki/Logical_graph Logical Graph], [http://en.wikiversity.org/ Wikiversity] | ||
| + | * [http://beta.wikiversity.org/wiki/Logical_graph Logical Graph], [http://beta.wikiversity.org/ Wikiversity Beta] | ||
| + | * [http://en.wikipedia.org/w/index.php?title=Logical_graph&oldid=67277491 Logical Graph], [http://en.wikipedia.org/ Wikipedia] | ||
| + | [[Category:Artificial Intelligence]] | ||
| + | [[Category:Boolean Functions]] | ||
| + | [[Category:Charles Sanders Peirce]] | ||
[[Category:Combinatorics]] | [[Category:Combinatorics]] | ||
[[Category:Computer Science]] | [[Category:Computer Science]] | ||
[[Category:Cybernetics]] | [[Category:Cybernetics]] | ||
| + | [[Category:Equational Reasoning]] | ||
[[Category:Formal Languages]] | [[Category:Formal Languages]] | ||
[[Category:Formal Systems]] | [[Category:Formal Systems]] | ||
| + | [[Category:George Spencer Brown]] | ||
[[Category:Graph Theory]] | [[Category:Graph Theory]] | ||
[[Category:History of Logic]] | [[Category:History of Logic]] | ||
[[Category:History of Mathematics]] | [[Category:History of Mathematics]] | ||
| + | [[Category:Inquiry]] | ||
| + | [[Category:Knowledge Representation]] | ||
| + | [[Category:Laws of Form]] | ||
[[Category:Logic]] | [[Category:Logic]] | ||
| + | [[Category:Logical Graphs]] | ||
[[Category:Mathematics]] | [[Category:Mathematics]] | ||
[[Category:Philosophy]] | [[Category:Philosophy]] | ||
| + | [[Category:Propositional Calculus]] | ||
[[Category:Semiotics]] | [[Category:Semiotics]] | ||
[[Category:Visualization]] | [[Category:Visualization]] | ||
Latest revision as of 14:26, 6 November 2015
☞ This page belongs to resource collections on Logic and Inquiry.
A logical graph is a graph-theoretic structure in one of the systems of graphical syntax that Charles Sanders Peirce developed for logic.
In his papers on qualitative logic, entitative graphs, and existential graphs, Peirce developed several versions of a graphical formalism, or a graph-theoretic formal language, designed to be interpreted for logic.
In the century since Peirce initiated this line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph-theoretic structures. This article examines the common basis of these formal systems from a bird's eye view, focusing on those aspects of form that are shared by the entire family of algebras, calculi, or languages, however they happen to be viewed in a given application.
Abstract point of view
| Wollust ward dem Wurm gegeben … | |
| — Friedrich Schiller, An die Freude |
The bird's eye view in question is more formally known as the perspective of formal equivalence, from which remove one cannot see many distinctions that appear momentous from lower levels of abstraction. In particular, expressions of different formalisms whose syntactic structures are isomorphic from the standpoint of algebra or topology are not recognized as being different from each other in any significant sense. Though we may note in passing such historical details as the circumstance that Charles Sanders Peirce used a streamer-cross symbol where George Spencer Brown used a carpenter's square marker, the theme of principal interest at the abstract level of form is neutral with regard to variations of that order.
In lieu of a beginning
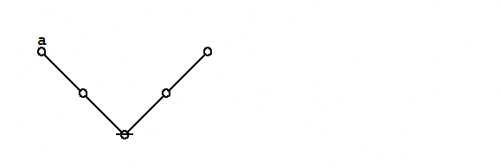
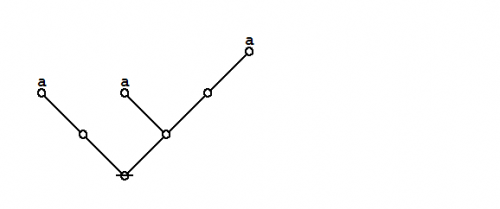
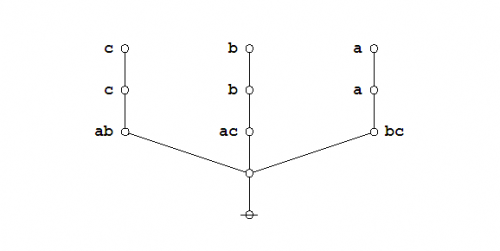
Consider the formal equations indicated in Figures 1 and 2.
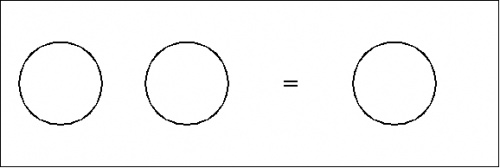 |
(1) |
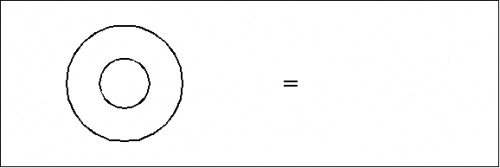 |
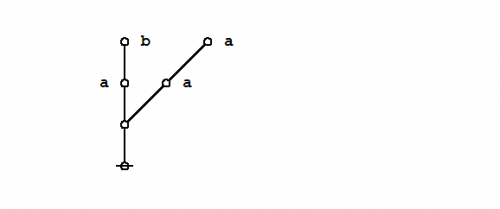
(2) |
For the time being these two forms of transformation may be referred to as axioms or initial equations.
Duality : logical and topological
There are two types of duality that have to be kept separately mind in the use of logical graphs — logical duality and topological duality.
There is a standard way that graphs of the order that Peirce considered, those embedded in a continuous manifold like that commonly represented by a plane sheet of paper — with or without the paper bridges that Peirce used to augment its topological genus — can be represented in linear text as what are called parse strings or traversal strings and parsed into pointer structures in computer memory.
A blank sheet of paper can be represented in linear text as a blank space, but that way of doing it tends to be confusing unless the logical expression under consideration is set off in a separate display.
For example, consider the axiom or initial equation that is shown below:
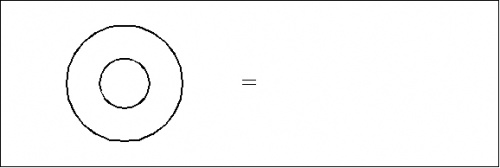 |
(3) |
This can be written inline as \({}^{\backprime\backprime} \texttt{( ( ) )} = \quad {}^{\prime\prime}\!\) or set off in a text display as follows:
| \(\texttt{( ( ) )}\!\) | \(=\!\) |
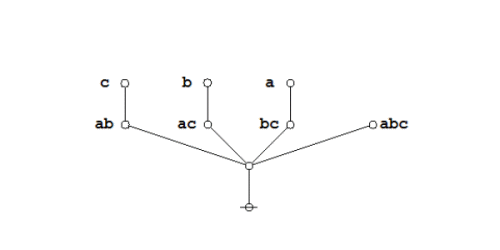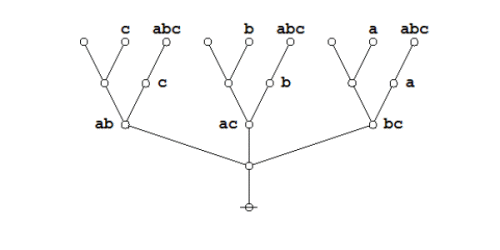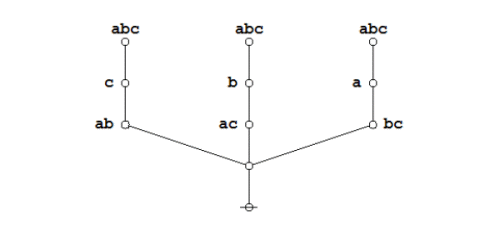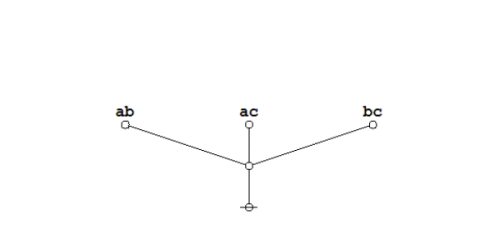
When we turn to representing the corresponding expressions in computer memory, where they can be manipulated with utmost facility, we begin by transforming the planar graphs into their topological duals. The planar regions of the original graph correspond to nodes (or points) of the dual graph, and the boundaries between planar regions in the original graph correspond to edges (or lines) between the nodes of the dual graph.
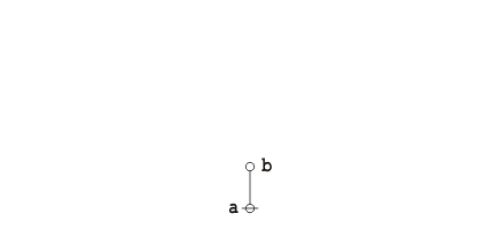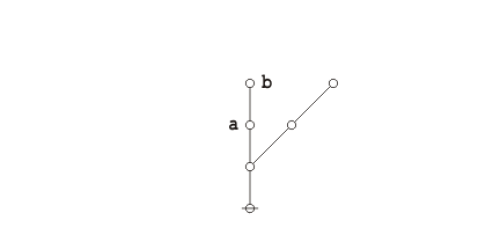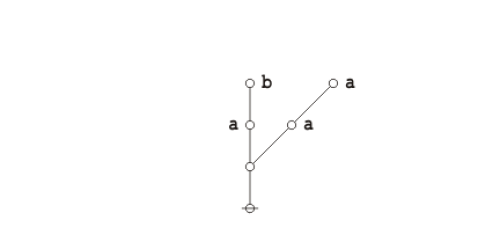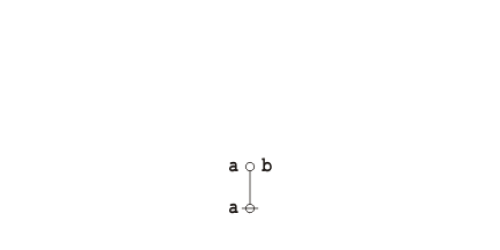
For example, overlaying the corresponding dual graphs on the plane-embedded graphs shown above, we get the following composite picture:
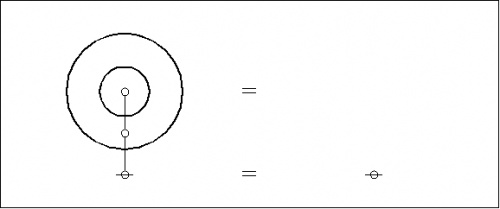 |
(4) |
Though it's not really there in the most abstract topology of the matter, for all sorts of pragmatic reasons we find ourselves compelled to single out the outermost region of the plane in a distinctive way and to mark it as the root node of the corresponding dual graph. In the present style of Figure the root nodes are marked by horizontal strike-throughs.
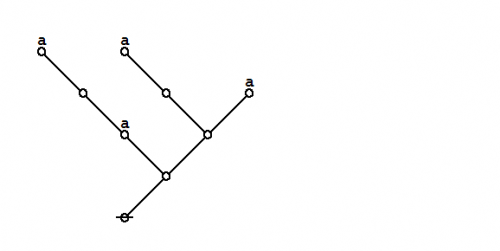
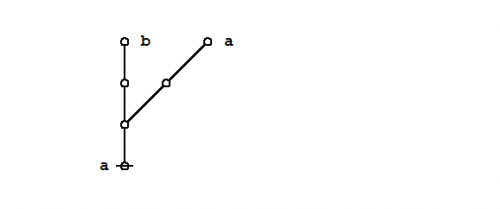
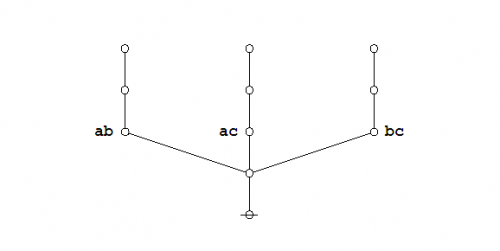
Extracting the dual graphs from their composite matrices, we get this picture:
 |
(5) |
It is easy to see the relationship between the parenthetical expressions of Peirce's logical graphs, that somewhat clippedly picture the ordered containments of their formal contents, and the associated dual graphs, that constitute the species of rooted trees here to be described.
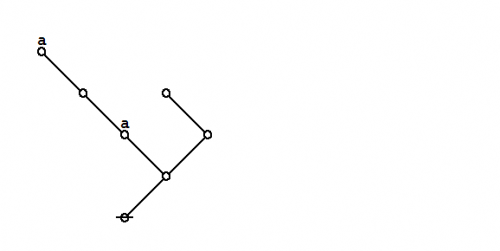
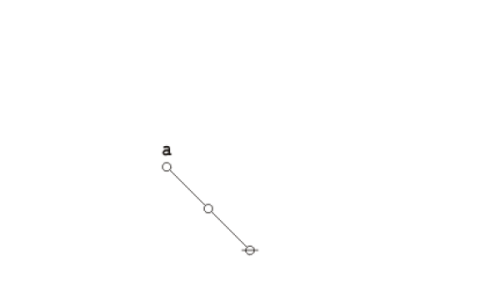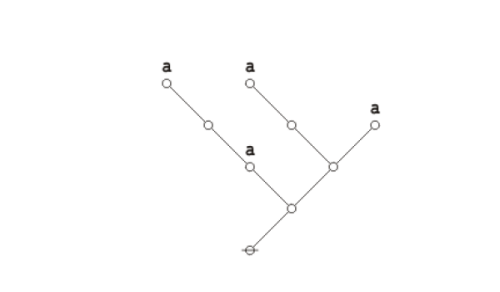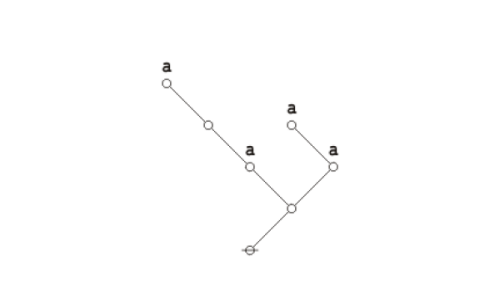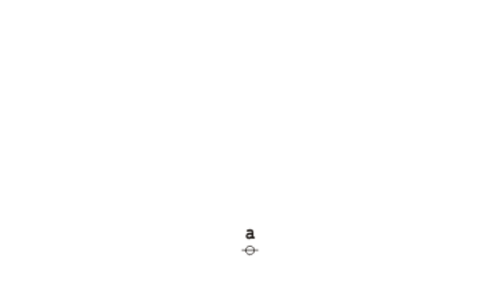
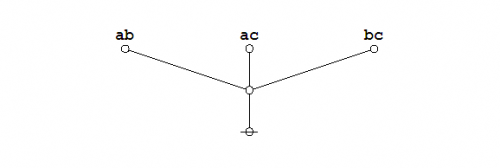
In the case of our last example, a moment's contemplation of the following picture will lead us to see that we can get the corresponding parenthesis string by starting at the root of the tree, climbing up the left side of the tree until we reach the top, then climbing back down the right side of the tree until we return to the root, all the while reading off the symbols, in this case either \({}^{\backprime\backprime} \texttt{(} {}^{\prime\prime}\!\) or \({}^{\backprime\backprime} \texttt{)} {}^{\prime\prime},\!\) that we happen to encounter in our travels.
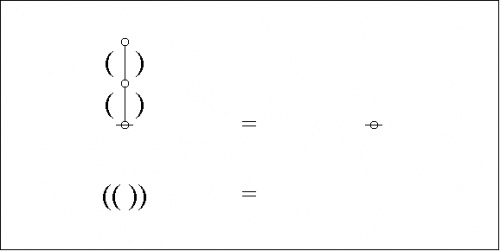 |
(6) |
This ritual is called traversing the tree, and the string read off is called the traversal string of the tree. The reverse ritual, that passes from the string to the tree, is called parsing the string, and the tree constructed is called the parse graph of the string. The speakers thereof tend to be a bit loose in this language, often using parse string to mean the string that gets parsed into the associated graph.
We have treated in some detail various forms of the initial equation or logical axiom that is formulated in string form as \({}^{\backprime\backprime} \texttt{( ( ) )} = \quad {}^{\prime\prime}.~\!\) For the sake of comparison, let's record the plane-embedded and topological dual forms of the axiom that is formulated in string form as \({}^{\backprime\backprime} \texttt{( )( )} = \texttt{( )} {}^{\prime\prime}.\!\)
First the plane-embedded maps:
 |
(7) |
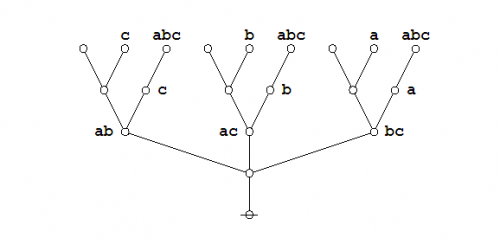
Next the plane-embedded maps and their dual trees superimposed:
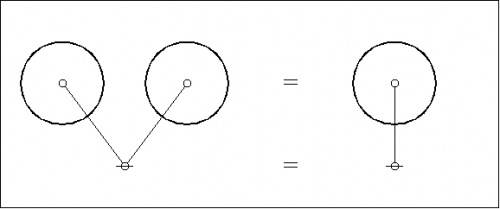 |
(8) |
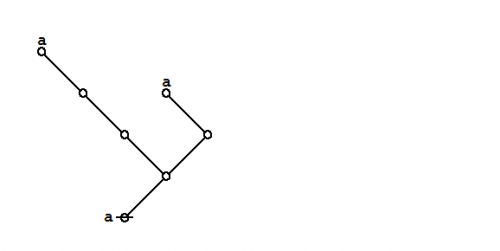
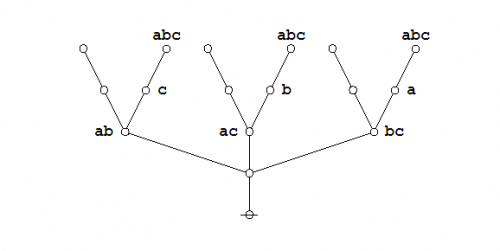
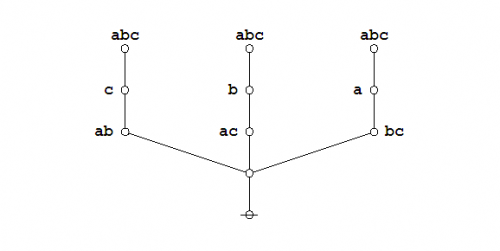
Finally the dual trees by themselves:
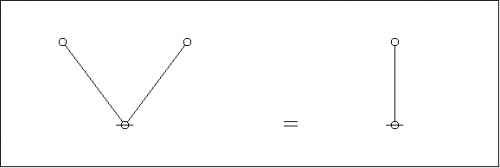 |
(9) |
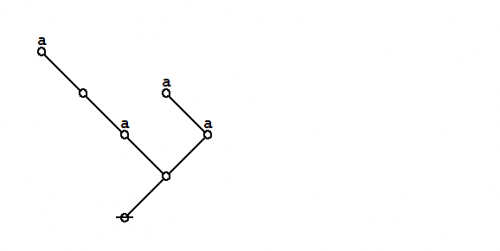
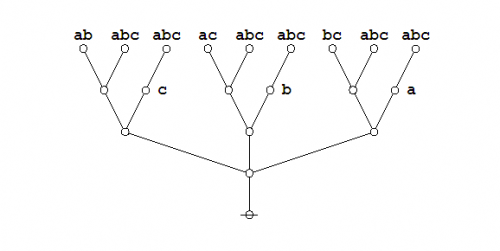
And here are the parse trees with their traversal strings indicated:
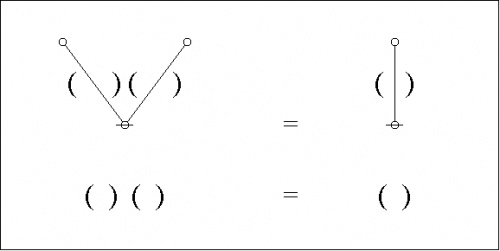 |
(10) |
We have at this point enough material to begin thinking about the forms of analogy, iconicity, metaphor, morphism, whatever you want to call them, that are pertinent to the use of logical graphs in their various logical interpretations, for instance, those that Peirce described as entitative graphs and existential graphs.
Computational representation
The parse graphs that we've been looking at so far bring us one step closer to the pointer graphs that it takes to make these maps and trees live in computer memory, but they are still a couple of steps too abstract to detail the concrete species of dynamic data structures that we need. The time has come to flesh out the skeletons that we've drawn up to this point.
Nodes in a graph represent records in computer memory. A record is a collection of data that can be conceived to reside at a specific address. The address of a record is analogous to a demonstrative pronoun, on which account programmers commonly describe it as a pointer and semioticians recognize it as a type of sign called an index.
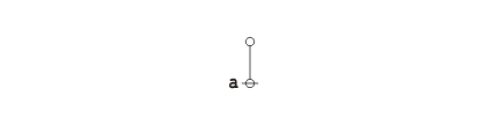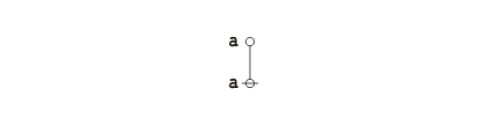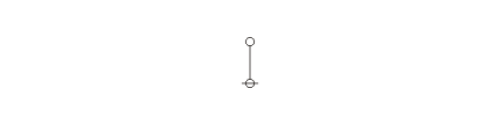
At the next level of concreteness, a pointer-record structure is represented as follows:
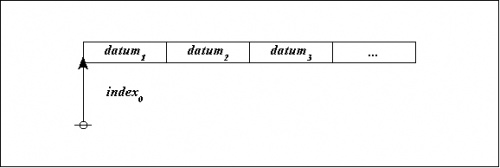 |
(11) |
This portrays the pointer \(\mathit{index}_0\!\) as the address of a record that contains the following data:
| \(\mathit{datum}_1, \mathit{datum}_2, \mathit{datum}_3, \ldots,\!\) and so on. |
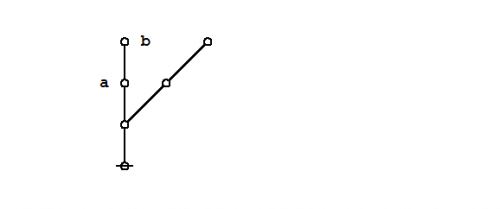
What makes it possible to represent graph-theoretical structures as data structures in computer memory is the fact that an address is just another datum, and so we may have a state of affairs like the following:
 |
(12) |
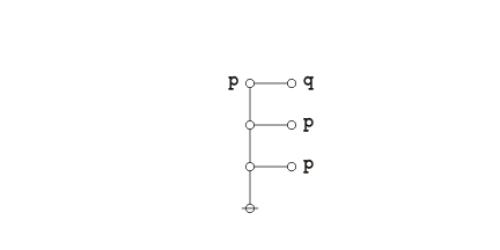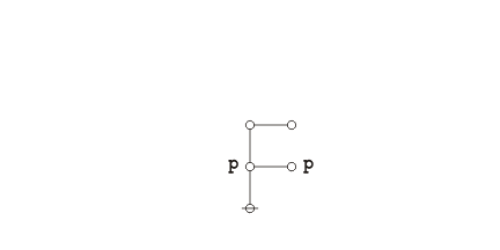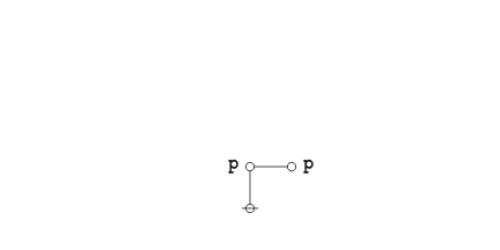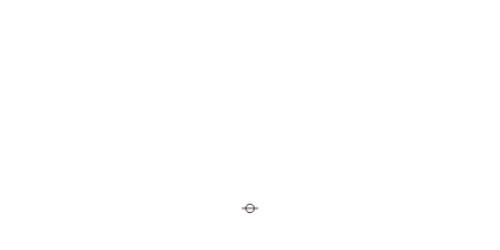
Returning to the abstract level, it takes three nodes to represent the three data records illustrated above: one root node connected to a couple of adjacent nodes. The items of data that do not point any further up the tree are then treated as labels on the record-nodes where they reside, as shown below:
 |
(13) |
Notice that drawing the arrows is optional with rooted trees like these, since singling out a unique node as the root induces a unique orientation on all the edges of the tree, with up being the same direction as away from the root.
Quick tour of the neighborhood
This much preparation allows us to take up the founding axioms or initial equations that determine the entire system of logical graphs.
Primary arithmetic as semiotic system
Though it may not seem too exciting, logically speaking, there are many reasons to make oneself at home with the system of forms that is represented indifferently, topologically speaking, by rooted trees, balanced strings of parentheses, or finite sets of non-intersecting simple closed curves in the plane.
- One reason is that it gives us a respectable example of a sign domain on which to cut our semiotic teeth, non-trivial in the sense that it contains a countable infinity of signs.
- Another reason is that it allows us to study a simple form of computation that is recognizable as a species of semiosis, or sign-transforming process.
This space of forms, along with the two axioms that induce its partition into exactly two equivalence classes, is what George Spencer Brown called the primary arithmetic.
The axioms of the primary arithmetic are shown below, as they appear in both graph and string forms, along with pairs of names that come in handy for referring to the two opposing directions of applying the axioms.
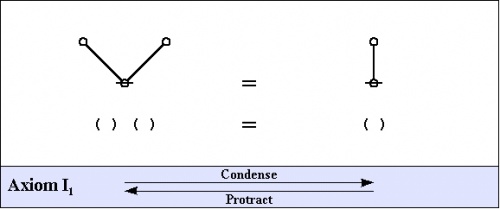 |
(14) |
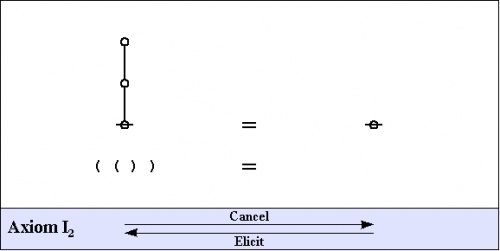 |
(15) |
Let \(S\!\) be the set of rooted trees and let \(S_0\!\) be the 2-element subset of \(S\!\) that consists of a rooted node and a rooted edge.
| \(S\!\) | \(=\!\) | \(\{ \text{rooted trees} \}\!\) |
| \(S_0\!\) | \(=\!\) | \(\{ \ominus, \vert \} = \{\!\) |
Simple intuition, or a simple inductive proof, assures us that any rooted tree can be reduced by way of the arithmetic initials either to a root node ![]() or else to a rooted edge
or else to a rooted edge ![]() .
.
For example, consider the reduction that proceeds as follows:
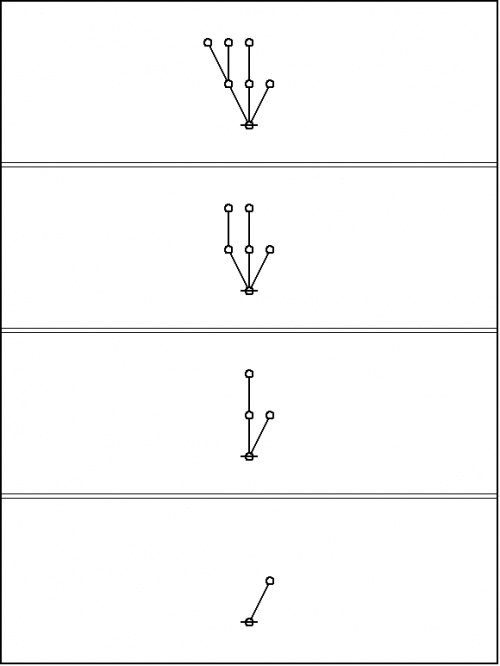 |
(16) |
Regarded as a semiotic process, this amounts to a sequence of signs, every one after the first serving as the interpretant of its predecessor, ending in a final sign that may be taken as the canonical sign for their common object, in the upshot being the result of the computation process. Simple as it is, this exhibits the main features of any computation, namely, a semiotic process that proceeds from an obscure sign to a clear sign of the same object, being in its aim and effect an action on behalf of clarification.
Primary algebra as pattern calculus
Experience teaches that complex objects are best approached in a gradual, laminar, modular fashion, one step, one layer, one piece at a time, and it's just as much the case when the complexity of the object is irreducible, that is, when the articulations of the representation are necessarily at joints that are cloven disjointedly from nature, with some assembly required in the synthetic integrity of the intuition.
That's one good reason for spending so much time on the first half of zeroth order logic, represented here by the primary arithmetic, a level of formal structure that C.S. Peirce verged on intuiting at numerous points and times in his work on logical graphs, and that Spencer Brown named and brought more completely to life.
There is one other reason for lingering a while longer in these primitive forests, and this is that an acquaintance with “bare trees”, those as yet unadorned with literal or numerical labels, will provide a firm basis for understanding what's really at issue in such problems as the “ontological status of variables”.
It is probably best to illustrate this theme in the setting of a concrete case, which we can do by reviewing the previous example of reductive evaluation shown in Figure 16.
The observation of several semioses, or sign-transformations, of roughly this shape will most likely lead an observer with any observational facility whatever to notice that it doesn't really matter what sorts of branches happen to sprout from the side of the root aside from the lone edge that also grows there — the end result will always be the same.
Our observer might think to summarize the results of many such observations by introducing a label or variable to signify any shape of branch whatever, writing something like the following:
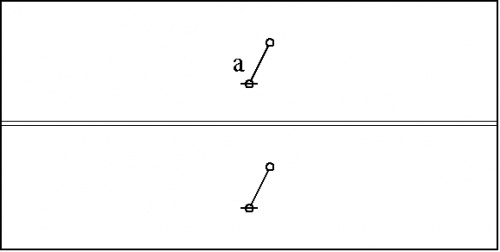 |
(17) |
Observations like that, made about an arithmetic of any variety, germinated by their summarizations, are the root of all algebra.
Speaking of algebra, and having encountered already one example of an algebraic law, we might as well introduce the axioms of the primary algebra, once again deriving their substance and their name from the works of Charles Sanders Peirce and George Spencer Brown, respectively.
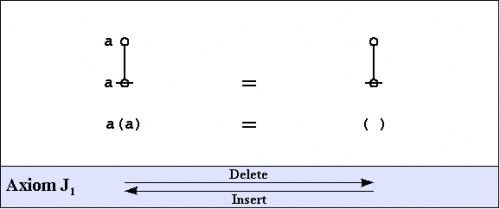 |
(18) |
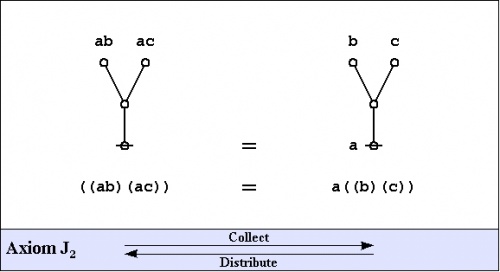 |
(19) |
The choice of axioms for any formal system is to some degree a matter of aesthetics, as it is commonly the case that many different selections of formal rules will serve as axioms to derive all the rest as theorems. As it happens, the example of an algebraic law that we noticed first, \(a \texttt{( )} = \texttt{( )},~\!\) as simple as it appears, proves to be provable as a theorem on the grounds of the foregoing axioms.
We might also notice at this point a subtle difference between the primary arithmetic and the primary algebra with respect to the grounds of justification that we have naturally if tacitly adopted for their respective sets of axioms.
The arithmetic axioms were introduced by fiat, in an a priori fashion, though of course it is only long prior experience with the practical uses of comparably developed generations of formal systems that would actually induce us to such a quasi-primal move. The algebraic axioms, in contrast, can be seen to derive their motive and their justice from the observation and summarization of patterns that are visible in the arithmetic spectrum.
Formal development
What precedes this point is intended as an informal introduction to the axioms of the primary arithmetic and primary algebra, and hopefully provides the reader with an intuitive sense of their motivation and rationale.
The next order of business is to give the exact forms of the axioms that are used in the following more formal development, devolving from Peirce's various systems of logical graphs via Spencer-Brown's Laws of Form (LOF). In formal proofs, a variation of the annotation scheme from LOF will be used to mark each step of the proof according to which axiom, or initial, is being invoked to justify the corresponding step of syntactic transformation, whether it applies to graphs or to strings.
Axioms
The axioms are just four in number, divided into the arithmetic initials, \(I_1\!\) and \(I_2,\!\) and the algebraic initials, \(J_1\!\) and \(J_2.\!\)
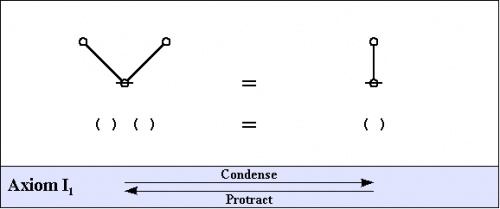 |
(20) |
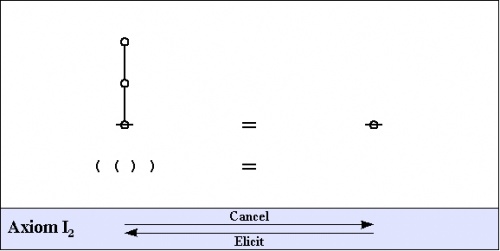 |
(21) |
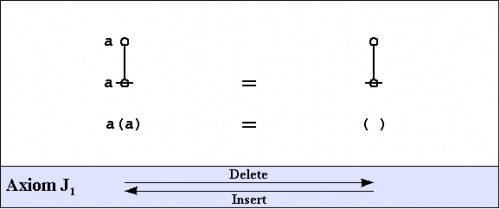 |
(22) |
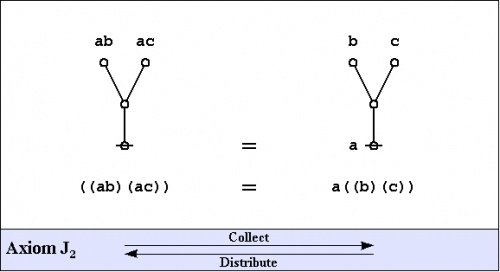 |
(23) |
One way of assigning logical meaning to the initial equations is known as the entitative interpretation (EN). Under EN, the axioms read as follows:
|
\(\begin{array}{ccccc} I_1 & : & \operatorname{true}\ \operatorname{or}\ \operatorname{true} & = & \operatorname{true} \\ I_2 & : & \operatorname{not}\ \operatorname{true}\ & = & \operatorname{false} \\ J_1 & : & a\ \operatorname{or}\ \operatorname{not}\ a & = & \operatorname{true} \\ J_2 & : & (a\ \operatorname{or}\ b)\ \operatorname{and}\ (a\ \operatorname{or}\ c) & = & a\ \operatorname{or}\ (b\ \operatorname{and}\ c) \\ \end{array}\) |
Another way of assigning logical meaning to the initial equations is known as the existential interpretation (EX). Under EX, the axioms read as follows:
|
\(\begin{array}{ccccc} I_1 & : & \operatorname{false}\ \operatorname{and}\ \operatorname{false} & = & \operatorname{false} \\ I_2 & : & \operatorname{not}\ \operatorname{false} & = & \operatorname{true} \\ J_1 & : & a\ \operatorname{and}\ \operatorname{not}\ a & = & \operatorname{false} \\ J_2 & : & (a\ \operatorname{and}\ b)\ \operatorname{or}\ (a\ \operatorname{and}\ c) & = & a\ \operatorname{and}\ (b\ \operatorname{or}\ c) \\ \end{array}\) |
All of the axioms in this set have the form of equations. This means that all of the inference steps that they allow are reversible. The proof annotation scheme employed below makes use of a double bar \(=\!=\!=\!=\!=\!=\) to mark this fact, although it will often be left to the reader to decide which of the two possible directions is the one required for applying the indicated axiom.
Frequently used theorems
The actual business of proof is a far more strategic affair than the simple cranking of inference rules might suggest. Part of the reason for this lies in the circumstance that the usual brands of inference rules combine the moving forward of a state of inquiry with the losing of information along the way that doesn't appear to be immediately relevant, at least, not as viewed in the local focus and the short run of the moment to moment proceedings of the proof in question. Over the long haul, this has the pernicious side-effect that one is forever strategically required to reconstruct much of the information that one had strategically thought to forget in earlier stages of the proof, if "before the proof started" can be counted as an earlier stage of the proof in view.
For this reason, among others, it is very instructive to study equational inference rules of the sort that our axioms have just provided. Although equational forms of reasoning are paramount in mathematics, they are less familiar to the student of conventional logic textbooks, who may find a few surprises here.
By way of gaining a minimal experience with how equational proofs look in the present forms of syntax, let us examine the proofs of a few essential theorems in the primary algebra.
C1. Double negation
The first theorem goes under the names of Consequence 1 \((C_1)\!\), the double negation theorem (DNT), or Reflection.
 |
(24) |
The proof that follows is adapted from the one that was given by George Spencer Brown in his book Laws of Form (LOF) and credited to two of his students, John Dawes and D.A. Utting.
|
(25) |
The steps of this proof are replayed in the following animation.
|
(26) |
C2. Generation theorem
One theorem of frequent use goes under the nickname of the weed and seed theorem (WAST). The proof is just an exercise in mathematical induction, once a suitable basis is laid down, and it will be left as an exercise for the reader. What the WAST says is that a label can be freely distributed or freely erased anywhere in a subtree whose root is labeled with that label. The second in our list of frequently used theorems is in fact the base case of this weed and seed theorem. In LOF, it goes by the names of Consequence 2 \((C_2)\!\) or Generation.
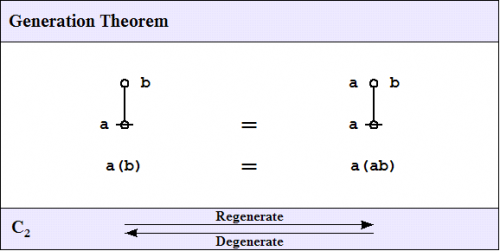 |
(27) |
Here is a proof of the Generation Theorem.
|
(28) |
The steps of this proof are replayed in the following animation.
|
(29) |
C3. Dominant form theorem
The third of the frequently used theorems of service to this survey is one that Spencer-Brown annotates as Consequence 3 \((C_3)\!\) or Integration. A better mnemonic might be dominance and recession theorem (DART), but perhaps the brevity of dominant form theorem (DFT) is sufficient reminder of its double-edged role in proofs.
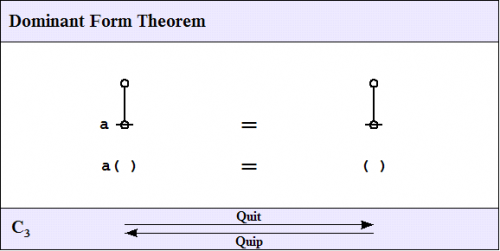 |
(30) |
Here is a proof of the Dominant Form Theorem.
|
(31) |
The following animation provides an instant re*play.
|
(32) |
Exemplary proofs
Based on the axioms given at the outest, and aided by the theorems recorded so far, it is possible to prove a multitude of much more complex theorems. A couple of all-time favorites are given next.
Peirce's law
- Main article : Peirce's law
Peirce's law is commonly written in the following form:
| \(((p \Rightarrow q) \Rightarrow p) \Rightarrow p\!\) |
The existential graph representation of Peirce's law is shown in Figure 33.
 |
(33) |
A graphical proof of Peirce's law is shown in Figure 34.
|
(34) |
The following animation replays the steps of the proof.
|
(35) |
Praeclarum theorema
An illustrious example of a propositional theorem is the praeclarum theorema, the admirable, shining, or splendid theorem of Leibniz.
|
If a is b and d is c, then ad will be bc. This is a fine theorem, which is proved in this way: a is b, therefore ad is bd (by what precedes), d is c, therefore bd is bc (again by what precedes), ad is bd, and bd is bc, therefore ad is bc. Q.E.D. (Leibniz, Logical Papers, p. 41). |
Under the existential interpretation, the praeclarum theorema is represented by means of the following logical graph.
 |
(36) |
And here's a neat proof of that nice theorem.
|
(37) |
The steps of the proof are replayed in the following animation.
|
(38) |
Two-thirds majority function
Consider the following equation in boolean algebra, posted as a problem for proof at MathOverFlow.
|
\(\begin{matrix} a b \bar{c} + a \bar{b} c + \bar{a} b c + a b c \\[6pt] \iff \\[6pt] a b + a c + b c \end{matrix}\) |
The required equation can be proven in the medium of logical graphs as shown in the following Figure.
|
(39) |
Here's an animated recap of the graphical transformations that occur in the above proof:
|
(40) |
Bibliography
- Leibniz, G.W. (1679–1686 ?), “Addenda to the Specimen of the Universal Calculus”, pp. 40–46 in G.H.R. Parkinson (ed. and trans., 1966), Leibniz : Logical Papers, Oxford University Press, London, UK.
- Peirce, C.S. (1931–1935, 1958), Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA. Cited as (CP volume.paragraph).
- Peirce, C.S. (1981–), Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN. Cited as (CE volume, page).
- Peirce, C.S. (1885), “On the Algebra of Logic : A Contribution to the Philosophy of Notation”, American Journal of Mathematics 7 (1885), 180–202. Reprinted as CP 3.359–403 and CE 5, 162–190.
- Peirce, C.S. (c. 1886), “Qualitative Logic”, MS 736. Published as pp. 101–115 in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, Volume 4, Mathematical Philosophy, Mouton, The Hague.
- Peirce, C.S. (1886 a), “Qualitative Logic”, MS 582. Published as pp. 323–371 in Writings of Charles S. Peirce : A Chronological Edition, Volume 5, 1884–1886, Peirce Edition Project (eds.), Indiana University Press, Bloomington, IN, 1993.
- Peirce, C.S. (1886 b), “The Logic of Relatives : Qualitative and Quantitative”, MS 584. Published as pp. 372–378 in Writings of Charles S. Peirce : A Chronological Edition, Volume 5, 1884–1886, Peirce Edition Project (eds.), Indiana University Press, Bloomington, IN, 1993.
- Spencer Brown, George (1969), Laws of Form, George Allen and Unwin, London, UK.
Resources
- Bergman and Paavola (eds.), Commens Dictionary of Peirce's Terms
- Dau, Frithjof
- Peirce's Existential Graphs : Readings and Links
- Existential Graphs as Moving Pictures of Thought — Computer Animated Proof of Leibniz's Praeclarum Theorema
- Shoup, Richard (ed.), Laws of Form Web Site
- Spencer-Brown, George (1973), Transcript Session One, AUM Conference, Esalen, CA.
Translations
Syllabus
Focal nodes
Peer nodes
- Logical Graph @ InterSciWiki
- Logical Graph @ MyWikiBiz
- Logical Graph @ Subject Wikis
- Logical Graph @ Wikiversity
- Logical Graph @ Wikiversity Beta
Logical operators
Template:Col-breakTemplate:Col-breakTemplate:Col-endRelated topics
- Propositional calculus
- Sole sufficient operator
- Truth table
- Universe of discourse
- Zeroth order logic
Relational concepts
Information, Inquiry
Related articles
- Differential Logic : Introduction
- Differential Propositional Calculus
- Differential Logic and Dynamic Systems
- Prospects for Inquiry Driven Systems
- Introduction to Inquiry Driven Systems
- Inquiry Driven Systems : Inquiry Into Inquiry
Document history
Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.
- Logical Graph, InterSciWiki
- Logical Graph, MyWikiBiz
- Logical Graph 1, PlanetMath
- Logical Graph 2, PlanetMath
- Logical Graph, Semantic Web
- Logical Graph, Wikinfo
- Logical Graph, Wikiversity
- Logical Graph, Wikiversity Beta
- Logical Graph, Wikipedia
- Artificial Intelligence
- Boolean Functions
- Charles Sanders Peirce
- Combinatorics
- Computer Science
- Cybernetics
- Equational Reasoning
- Formal Languages
- Formal Systems
- George Spencer Brown
- Graph Theory
- History of Logic
- History of Mathematics
- Inquiry
- Knowledge Representation
- Laws of Form
- Logic
- Logical Graphs
- Mathematics
- Philosophy
- Propositional Calculus
- Semiotics
- Visualization