Difference between revisions of "Directory:Jon Awbrey/Papers/Functional Logic : Inquiry and Analogy"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) (looks like the math parser might be working again) |
||
| (25 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{DISPLAYTITLE:Functional Logic : Inquiry and Analogy}} | {{DISPLAYTITLE:Functional Logic : Inquiry and Analogy}} | ||
| + | |||
| + | '''Author: [[User:Jon Awbrey|Jon Awbrey]]''' | ||
| + | |||
==Abstract== | ==Abstract== | ||
This report discusses C.S. Peirce's treatment of analogy, placing it in relation to his overall theory of inquiry. The first order of business is to introduce the three fundamental types of reasoning that Peirce adopted from classical logic. In Peirce's analysis both inquiry and analogy are complex programs of reasoning that develop through stages of these three types, although normally in different orders. | This report discusses C.S. Peirce's treatment of analogy, placing it in relation to his overall theory of inquiry. The first order of business is to introduce the three fundamental types of reasoning that Peirce adopted from classical logic. In Peirce's analysis both inquiry and analogy are complex programs of reasoning that develop through stages of these three types, although normally in different orders. | ||
| − | '''Note on notation.''' The discussion that follows uses [[minimal negations]], expressed as bracketed tuples of the form <math>\texttt{(} e_1 \texttt{,} \ldots \texttt{,} e_k \texttt{)},</math> and logical conjunctions, expressed as concatenated tuples of the form <math>e_1 ~\ldots~ e_k,</math> as the sole expression-forming operations of a calculus for [[boolean-valued functions]] or ''propositions''. The expressions of this calculus parse into data structures whose underlying graphs are called ''cacti'' by graph theorists. Hence the name ''[[cactus language]]'' for this dialect of propositional calculus. | + | '''Note on notation.''' The discussion that follows uses [[minimal negations]], expressed as bracketed tuples of the form <math>\texttt{(} e_1 \texttt{,} \ldots \texttt{,} e_k \texttt{)},\!</math> and logical conjunctions, expressed as concatenated tuples of the form <math>e_1 ~\ldots~ e_k,\!</math> as the sole expression-forming operations of a calculus for [[boolean-valued functions]] or ''propositions''. The expressions of this calculus parse into data structures whose underlying graphs are called ''cacti'' by graph theorists. Hence the name ''[[cactus language]]'' for this dialect of propositional calculus. |
<div class="nonumtoc">__TOC__</div> | <div class="nonumtoc">__TOC__</div> | ||
| Line 15: | Line 18: | ||
| [[Image:Types of Reasoning in Aristotle.jpg|600px]] | | [[Image:Types of Reasoning in Aristotle.jpg|600px]] | ||
|- | |- | ||
| − | | <math>\text{Figure 1. Types of Reasoning in Aristotle}</math> | + | | <math>\text{Figure 1. Types of Reasoning in Aristotle}\!</math> |
|} | |} | ||
| Line 25: | Line 28: | ||
| We have then three different kinds of inference: | | We have then three different kinds of inference: | ||
|- | |- | ||
| − | | Deduction or inference ''à priori'', | + | | Deduction or inference ''à priori'', |
|- | |- | ||
| − | | Induction or inference ''à particularis'', | + | | Induction or inference ''à particularis'', |
|- | |- | ||
| − | | Hypothesis or inference ''à posteriori''. | + | | Hypothesis or inference ''à posteriori''. |
|- | |- | ||
| align="right" | (Peirce, CE 1, p. 267). | | align="right" | (Peirce, CE 1, p. 267). | ||
| Line 35: | Line 38: | ||
{| align="center" width="90%" | {| align="center" width="90%" | ||
| − | | If I reason that certain conduct is wise because it has a character which belongs ''only'' to wise things, I reason ''à priori''. | + | | If I reason that certain conduct is wise because it has a character which belongs ''only'' to wise things, I reason ''à priori''. |
|- | |- | ||
| − | | If I think it is wise because it once turned out to be wise, that is, if I infer that it is wise on this occasion because it was wise on that occasion, I reason inductively [''à particularis'']. | + | | If I think it is wise because it once turned out to be wise, that is, if I infer that it is wise on this occasion because it was wise on that occasion, I reason inductively [''à particularis'']. |
|- | |- | ||
| − | | But if I think it is wise because a wise man does it, I then make the pure hypothesis that he does it because he is wise, and I reason ''à posteriori''. | + | | But if I think it is wise because a wise man does it, I then make the pure hypothesis that he does it because he is wise, and I reason ''à posteriori''. |
|- | |- | ||
| align="right" | (Peirce, CE 1, p. 180). | | align="right" | (Peirce, CE 1, p. 180). | ||
| Line 97: | Line 100: | ||
| [[Image:Triply Wise Act.jpg|400px]] | | [[Image:Triply Wise Act.jpg|400px]] | ||
|- | |- | ||
| − | | <math>\text{Figure 2. A Triply Wise Act}</math> | + | | <math>\text{Figure 2. A Triply Wise Act}\!</math> |
|} | |} | ||
| Line 113: | Line 116: | ||
| [[Image:Types of Reasoning in Transition.jpg|600px]] | | [[Image:Types of Reasoning in Transition.jpg|600px]] | ||
|- | |- | ||
| − | | <math>\text{Figure 3. Types of Reasoning in Transition}</math> | + | | <math>\text{Figure 3. Types of Reasoning in Transition}\!</math> |
|} | |} | ||
| Line 121: | Line 124: | ||
| [[Image:Types of Reasoning in Peirce.jpg|600px]] | | [[Image:Types of Reasoning in Peirce.jpg|600px]] | ||
|- | |- | ||
| − | | <math>\text{Figure 4. Types of Reasoning in Peirce}</math> | + | | <math>\text{Figure 4. Types of Reasoning in Peirce}\!</math> |
|} | |} | ||
| Line 245: | Line 248: | ||
<p> We have an Example (παραδειγμα, or analogy) when the major extreme is shown to be applicable to the middle term by means of a term similar to the third. It must be known both that the middle applies to the third term and that the first applies to the term similar to the third.</p> | <p> We have an Example (παραδειγμα, or analogy) when the major extreme is shown to be applicable to the middle term by means of a term similar to the third. It must be known both that the middle applies to the third term and that the first applies to the term similar to the third.</p> | ||
| − | <p> ''E.g.'', let A be “bad”, B “to make war on neighbors”, C “Athens against Thebes”, and D “Thebes against Phocis”. Then if we require to prove that war against Thebes is bad, we must be satisfied that war against neighbors is bad. Evidence of this can be drawn from similar examples, ''e.g.'', that war by Thebes against Phocis is bad. Then since war against neighbors is bad, and war against Thebes is against neighbors, it is evident that war against Thebes is bad. | + | <p> ''E.g.'', let A be “bad”, B “to make war on neighbors”, C “Athens against Thebes”, and D “Thebes against Phocis”. Then if we require to prove that war against Thebes is bad, we must be satisfied that war against neighbors is bad. Evidence of this can be drawn from similar examples, ''e.g.'', that war by Thebes against Phocis is bad. Then since war against neighbors is bad, and war against Thebes is against neighbors, it is evident that war against Thebes is bad.</p> |
|- | |- | ||
| align="right" | (Aristotle, “Prior Analytics” 2.24) | | align="right" | (Aristotle, “Prior Analytics” 2.24) | ||
| Line 253: | Line 256: | ||
| [[Image:Aristotle's Paradigm.jpg|600px]] | | [[Image:Aristotle's Paradigm.jpg|600px]] | ||
|- | |- | ||
| − | | <math>\operatorname{Figure~6.~Aristotle's~Paradigm}</math> | + | | <math>\operatorname{Figure~6.~Aristotle's} ~ {}^{\backprime\backprime}\text{Paradigm}{}^{\prime\prime}\!</math> |
|} | |} | ||
| Line 264: | Line 267: | ||
{| align="center" width="90%" | {| align="center" width="90%" | ||
| | | | ||
| − | <p>The formula of analogy is as follows: <math>S^{\prime}, S^{\prime\prime}, ~\operatorname{and}~ S^{\prime\prime\prime}</math> are taken at random from such a class that their characters at random are such as <math>P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}.</math></p> | + | <p>The formula of analogy is as follows: <math>S^{\prime}, S^{\prime\prime}, ~\operatorname{and}~ S^{\prime\prime\prime}\!</math> are taken at random from such a class that their characters at random are such as <math>{P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}}.\!</math></p> |
|- | |- | ||
| | | | ||
| Line 277: | Line 280: | ||
</center> | </center> | ||
|- | |- | ||
| − | | <p>Such an argument is double. It combines the two following: | + | | <p>Such an argument is double. It combines the two following:</p> |
|- | |- | ||
| | | | ||
| Line 323: | Line 326: | ||
| [[Image:Peirce's Formulation of Analogy (Version 1).jpg|600px]] | | [[Image:Peirce's Formulation of Analogy (Version 1).jpg|600px]] | ||
|- | |- | ||
| − | | <math>\operatorname{Figure~7.~Peirce's~Formulation~of~Analogy~(Version~1)}</math> | + | | <math>\operatorname{Figure~7.~Peirce's~Formulation~of~Analogy~(Version~1)}\!</math> |
|} | |} | ||
| Line 330: | Line 333: | ||
{| align="center" width="90%" | {| align="center" width="90%" | ||
| | | | ||
| − | <p>The formula of the analogical inference presents, therefore, three premisses, thus: <math>S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime},</math> are a random sample of some undefined class, <math>X,\!</math> of whose characters <math>P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime},</math> are samples,</p> | + | <p>The formula of the analogical inference presents, therefore, three premisses, thus: <math>S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime},\!</math> are a random sample of some undefined class, <math>X,\!</math> of whose characters <math>P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime},\!</math> are samples,</p> |
|- | |- | ||
| | | | ||
| Line 365: | Line 368: | ||
| | | | ||
<center> | <center> | ||
| − | <math>\text{Hence, deductively,}~ T ~\text{is a}~ Q.</math> | + | <math>\text{Hence, deductively,}~ T ~\text{is a}~ Q.\!</math> |
</center> | </center> | ||
|- | |- | ||
| Line 376: | Line 379: | ||
| [[Image:Peirce's Formulation of Analogy (Version 2).jpg|600px]] | | [[Image:Peirce's Formulation of Analogy (Version 2).jpg|600px]] | ||
|- | |- | ||
| − | | <math>\operatorname{Figure~8.~Peirce's~Formulation~of~Analogy~(Version~2)}</math> | + | | <math>\operatorname{Figure~8.~Peirce's~Formulation~of~Analogy~(Version~2)}\!</math> |
|} | |} | ||
| Line 397: | Line 400: | ||
| [[Image:Dewey's Sign of Rain Example.jpg|600px]] | | [[Image:Dewey's Sign of Rain Example.jpg|600px]] | ||
|- | |- | ||
| − | | <math>\operatorname{Figure~9.~Dewey's} ~ {}^{\backprime\backprime}\text{Sign of Rain}{}^{\prime\prime} ~ \text{Example}</math> | + | | <math>\operatorname{Figure~9.~Dewey's} ~ {}^{\backprime\backprime}\text{Sign of Rain}{}^{\prime\prime} ~ \text{Example}\!</math> |
|} | |} | ||
| Line 407: | Line 410: | ||
| [[Image:Cycle of Inquiry.jpg|600px]] | | [[Image:Cycle of Inquiry.jpg|600px]] | ||
|- | |- | ||
| − | | <math>\text{Figure 10. The Cycle of Inquiry}</math> | + | | <math>\text{Figure 10. The Cycle of Inquiry}\!</math> |
|} | |} | ||
| − | # Abduction. The first, faltering step into the cycle of inquiry is taken through the flexion of abductive reasoning. The fact | + | # Abduction. The first, faltering step into the cycle of inquiry is taken through the flexion of abductive reasoning. The fact ''C'' ⇒ ''A'', the coolness of the air in the pedestrian's current situation, brings into play from his worldly experience (or from other kinds of background knowledge) the rule ''B'' ⇒ ''A'', that a chill in the air is a feature of situations that betoken rain. This fact and this rule, working in tandem, precipitate a plausible explanation for the observed phenomena. The hiker abduces the case ''C'' ⇒ ''B'', that bodes for rain in the current situation. |
# Deduction. … | # Deduction. … | ||
# Induction. … | # Induction. … | ||
| + | |||
| + | In this analysis of the first steps of Inquiry, we have a complex or a mixed form of inference that can be seen as taking place in two steps: | ||
| + | |||
| + | 1. The first step is an Abduction that abstracts a Case from the consideration of a Fact and a Rule. | ||
| + | |||
| + | {| | ||
| + | | width=36 | | ||
| + | | Fact: || ''C'' ⇒ ''A'', || In the Current situation the Air is cool. | ||
| + | |- | ||
| + | | | ||
| + | | Rule: || ''B'' ⇒ ''A'', || Just Before it rains, the Air is cool. | ||
| + | |- | ||
| + | | | ||
| + | | Case: || ''C'' ⇒ ''B'', || The Current situation is just Before it rains. | ||
| + | |} | ||
| + | |||
| + | 2. The final step is a Deduction that admits this Case to another Rule and so arrives at a novel Fact. | ||
| + | |||
| + | {| | ||
| + | | width=36 | | ||
| + | | Case: || ''C'' ⇒ ''B'', || The Current situation is just Before it rains. | ||
| + | |- | ||
| + | | | ||
| + | | Rule: || ''B'' ⇒ ''D'', || Just Before it rains, a Dark cloud will appear. | ||
| + | |- | ||
| + | | | ||
| + | | Fact: || ''C'' ⇒ ''D'', || In the Current situation, a Dark cloud will appear. | ||
| + | |} | ||
| + | |||
| + | This is nowhere near a complete analysis of the Rainy Day inquiry, even insofar as it might be carried out within the constraints of the syllogistic framework, and it covers only the first two steps of the relevant inquiry process, but maybe it will do for a start. | ||
==2. Functional Conception of Quantification Theory== | ==2. Functional Conception of Quantification Theory== | ||
| − | Up till now quantification theory has been based on the assumption of individual variables ranging over universal collections of perfectly determinate elements. Merely to write down quantified formulas like <math>\forall_{x \in X} f(x)</math> and <math>\exists_{x \in X} f(x)</math> involves a subscription to such notions, as shown by the membership relations invoked in their indices. Reflected on pragmatic and constructive principles, however, these ideas begin to appear as problematic hypotheses whose warrants are not beyond question, projects of exhaustive determination that overreach the powers of finite information and control to manage. Therefore, it is worth considering how we might shift the scene of quantification theory closer to familiar ground, toward the predicates themselves that represent our continuing acquaintance with phenomena. | + | Up till now quantification theory has been based on the assumption of individual variables ranging over universal collections of perfectly determinate elements. Merely to write down quantified formulas like <math>\forall_{x \in X} f(x)\!</math> and <math>\exists_{x \in X} f(x)\!</math> involves a subscription to such notions, as shown by the membership relations invoked in their indices. Reflected on pragmatic and constructive principles, however, these ideas begin to appear as problematic hypotheses whose warrants are not beyond question, projects of exhaustive determination that overreach the powers of finite information and control to manage. Therefore, it is worth considering how we might shift the scene of quantification theory closer to familiar ground, toward the predicates themselves that represent our continuing acquaintance with phenomena. |
===Higher Order Propositional Expressions=== | ===Higher Order Propositional Expressions=== | ||
| Line 424: | Line 457: | ||
====Higher Order Propositions and Logical Operators (''n'' = 1)==== | ====Higher Order Propositions and Logical Operators (''n'' = 1)==== | ||
| − | A ''higher order proposition'' is, very roughly speaking, a proposition about propositions. If the original order of propositions is a class of indicator functions <math>f : X \to \mathbb{B},</math> then the next higher order of propositions consists of maps of the type <math>m : (X \to \mathbb{B}) \to \mathbb{B}.</math> | + | A ''higher order proposition'' is, very roughly speaking, a proposition about propositions. If the original order of propositions is a class of indicator functions <math>{f : X \to \mathbb{B}},\!</math> then the next higher order of propositions consists of maps of the type <math>{m : (X \to \mathbb{B}) \to \mathbb{B}}.\!</math> |
| − | For example, consider the case where <math>X = \mathbb{B}.</math> Then there are exactly four propositions <math>f : \mathbb{B} \to \mathbb{B},</math> and exactly sixteen higher order propositions that are based on this set, all bearing the type <math>m : (\mathbb{B} \to \mathbb{B}) \to \mathbb{B}.</math> | + | For example, consider the case where <math>{X = \mathbb{B}}.\!</math> Then there are exactly four propositions <math>{f : \mathbb{B} \to \mathbb{B}},\!</math> and exactly sixteen higher order propositions that are based on this set, all bearing the type <math>{m : (\mathbb{B} \to \mathbb{B}) \to \mathbb{B}}.\!</math> |
| − | Table | + | Table 11 lists the sixteen higher order propositions about propositions on one boolean variable, organized in the following fashion: Columns 1 and 2 form a truth table for the four <math>{f : \mathbb{B} \to \mathbb{B}},\!</math> turned on its side from the way that one is most likely accustomed to see truth tables, with the row leaders in Column 1 displaying the names of the functions <math>{f_i},\!</math> for <math>{i}\!</math> = 1 to 4, while the entries in Column 2 give the values of each function for the argument values that are listed in the corresponding column head. Column 3 displays one of the more usual expressions for the proposition in question. The last sixteen columns are topped by a collection of conventional names for the higher order propositions, also known as the ''measures'' <math>{m_j},\!</math> for <math>{j}\!</math> = 0 to 15, where the entries in the body of the Table record the values that each <math>{m_j}\!</math> assigns to each <math>{f_i}.\!</math> |
{| align="center" border="1" cellpadding="4" cellspacing="0" style="background:white; color:black; font-weight:bold; text-align:center; width:90%" | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:white; color:black; font-weight:bold; text-align:center; width:90%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 11. Higher Order Propositions} ~~ (n = 1)\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| − | | align="right" | <math>x:</math> | + | | align="right" | <math>x:\!</math> |
| 1 0 | | 1 0 | ||
| <math>f\!</math> | | <math>f\!</math> | ||
| − | | <math>m_0</math> | + | | <math>m_0\!</math> |
| − | | <math>m_1</math> | + | | <math>m_1\!</math> |
| − | | <math>m_2</math> | + | | <math>m_2\!</math> |
| − | | <math>m_3</math> | + | | <math>m_3\!</math> |
| − | | <math>m_4</math> | + | | <math>m_4\!</math> |
| − | | <math>m_5</math> | + | | <math>m_5\!</math> |
| − | | <math>m_6</math> | + | | <math>m_6\!</math> |
| − | | <math>m_7</math> | + | | <math>m_7\!</math> |
| − | | <math>m_8</math> | + | | <math>m_8\!</math> |
| − | | <math>m_9</math> | + | | <math>m_9\!</math> |
| − | | <math>m_{10}</math> | + | | <math>m_{10}\!</math> |
| − | | <math>m_{11}</math> | + | | <math>m_{11}\!</math> |
| − | | <math>m_{12}</math> | + | | <math>m_{12}\!</math> |
| − | | <math>m_{13}</math> | + | | <math>m_{13}\!</math> |
| − | | <math>m_{14}</math> | + | | <math>m_{14}\!</math> |
| − | | <math>m_{15}</math> | + | | <math>m_{15}\!</math> |
| − | |- | + | |- |
| − | | <math>f_0</math> | + | | <math>f_0\!</math> |
| − | | 0 0 | + | | 0 0 |
| − | | <math>0\!</math> | + | | <math>0\!</math> |
| − | | 0 || style="background:black; color:white" | 1 | + | | 0 || style="background:black; color:white" | 1 |
| − | | 0 || style="background:black; color:white" | 1 | + | | 0 || style="background:black; color:white" | 1 |
| − | | 0 || style="background:black; color:white" | 1 | + | | 0 || style="background:black; color:white" | 1 |
| 0 || style="background:black; color:white" | 1 | | 0 || style="background:black; color:white" | 1 | ||
| 0 || style="background:black; color:white" | 1 | | 0 || style="background:black; color:white" | 1 | ||
| Line 465: | Line 499: | ||
| 0 || style="background:black; color:white" | 1 | | 0 || style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_1</math> | + | | <math>f_1\!</math> |
| 0 1 | | 0 1 | ||
| − | | <math>\texttt{(} x \texttt{)}</math> | + | | <math>\texttt{(} x \texttt{)}\!</math> |
| 0 || 0 | | 0 || 0 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 481: | Line 515: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_2</math> | + | | <math>f_2\!</math> |
| 1 0 | | 1 0 | ||
| <math>x\!</math> | | <math>x\!</math> | ||
| Line 495: | Line 529: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_3</math> | + | | <math>f_3\!</math> |
| 1 1 | | 1 1 | ||
| <math>1\!</math> | | <math>1\!</math> | ||
| Line 511: | Line 545: | ||
<br> | <br> | ||
| − | I am going to put off explaining Table | + | I am going to put off explaining Table 12, that presents a sample of what I call ''interpretive categories'' for higher order propositions, until after we get beyond the 1-dimensional case, since these lower dimensional cases tend to be a bit ''condensed'' or ''degenerate'' in their structures, and a lot of what is going on here will almost automatically become clearer as soon as we get even two logical variables into the mix. |
{| align="center" border="1" cellpadding="4" cellspacing="0" style="font-weight:bold; text-align:center; width:90%" | {| align="center" border="1" cellpadding="4" cellspacing="0" style="font-weight:bold; text-align:center; width:90%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 12. Interpretive Categories for Higher Order Propositions} ~~ (n = 1)~\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| Measure | | Measure | ||
| Line 657: | Line 692: | ||
====Higher Order Propositions and Logical Operators (''n'' = 2)==== | ====Higher Order Propositions and Logical Operators (''n'' = 2)==== | ||
| − | By way of reviewing notation and preparing to extend it to higher order universes of discourse, let us first consider the universe of discourse <math>X^\ | + | By way of reviewing notation and preparing to extend it to higher order universes of discourse, let us first consider the universe of discourse <math>X^\bullet = [\mathcal{X}] = [x_1, x_2] = [u, v],\!</math> based on two logical features or boolean variables <math>{u}\!</math> and <math>{v}.\!</math> |
| − | The universe of discourse <math>X^\ | + | The universe of discourse <math>{X^\bullet}\!</math> consists of two parts, a set of ''points'' and a set of ''propositions''. |
| − | The points of <math>X^\ | + | The points of <math>{X^\bullet}\!</math> form the space: |
{| align="center" cellpadding="8" | {| align="center" cellpadding="8" | ||
| − | | <math>X \quad = \quad \langle \mathcal{X} \rangle \quad = \quad \langle u, v \rangle \quad = \quad \{ (u, v) \} \quad \cong \quad \mathbb{B}^2.</math> | + | | <math>{X \quad = \quad \langle \mathcal{X} \rangle \quad = \quad \langle u, v \rangle \quad = \quad \{ (u, v) \} \quad \cong \quad \mathbb{B}^2}.~\!</math> |
|} | |} | ||
| − | Each point in <math>X\!</math> may be indicated by means of a ''singular proposition'', that is, a proposition that describes it uniquely. This form of representation leads to the following enumeration of points: | + | Each point in <math>{X}\!</math> may be indicated by means of a ''singular proposition'', that is, a proposition that describes it uniquely. This form of representation leads to the following enumeration of points: |
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| <math>X\!</math> | | <math>X\!</math> | ||
| <math>=\!</math> | | <math>=\!</math> | ||
| − | | <math>\{ ~ \texttt{(} u \texttt{)(} v \texttt{)} ~,~ \texttt{(} u \texttt{)} ~ v ~,~ u ~ \texttt{(} v \texttt{)} ~,~ u ~ v ~ \}</math> | + | | <math>\{ ~ \texttt{(} u \texttt{)(} v \texttt{)} ~,~ \texttt{(} u \texttt{)} ~ v ~,~ u ~ \texttt{(} v \texttt{)} ~,~ u ~ v ~ \}\!</math> |
| <math>\cong\!</math> | | <math>\cong\!</math> | ||
| − | | <math>\mathbb{B}^2,</math> | + | | <math>\mathbb{B}^2,\!</math> |
|} | |} | ||
| − | Each point in <math>X\!</math> may also be described by means of its ''coordinates'', that is, by the ordered pair of values in <math>\mathbb{B}</math> that the coordinate propositions <math>u\!</math> and <math>v\!</math> take on that point. This form of representation leads to the following enumeration of points: | + | Each point in <math>X\!</math> may also be described by means of its ''coordinates'', that is, by the ordered pair of values in <math>\mathbb{B}\!</math> that the coordinate propositions <math>u\!</math> and <math>v\!</math> take on that point. This form of representation leads to the following enumeration of points: |
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| <math>X\!</math> | | <math>X\!</math> | ||
| <math>=\!</math> | | <math>=\!</math> | ||
| − | | <math>\{\ (0, 0),\ (0, 1),\ (1, 0),\ (1, 1)\ \}</math> | + | | <math>\{\ (0, 0),\ (0, 1),\ (1, 0),\ (1, 1)\ \}\!</math> |
| <math>\cong\!</math> | | <math>\cong\!</math> | ||
| − | | <math>\mathbb{B}^2.</math> | + | | <math>\mathbb{B}^2.\!</math> |
|} | |} | ||
| − | The propositions of <math>X^\ | + | The propositions of <math>{X^\bullet}\!</math> form the space: |
{| align="center" cellpadding="8" | {| align="center" cellpadding="8" | ||
| − | | <math>X^\uparrow \quad = \quad (X \to \mathbb{B}) \quad = \quad \{ f : X \to \mathbb{B} \} \quad \cong \quad (\mathbb{B}^2 \to \mathbb{B}).</math> | + | | <math>X^\uparrow \quad = \quad (X \to \mathbb{B}) \quad = \quad \{ f : X \to \mathbb{B} \} \quad \cong \quad (\mathbb{B}^2 \to \mathbb{B}).\!</math> |
|} | |} | ||
As always, it is frequently convenient to omit a few of the finer markings of distinctions among isomorphic structures, so long as one is aware of their presence and knows when it is crucial to call upon them again. | As always, it is frequently convenient to omit a few of the finer markings of distinctions among isomorphic structures, so long as one is aware of their presence and knows when it is crucial to call upon them again. | ||
| − | The next higher order universe of discourse that is built on <math>X^\ | + | The next higher order universe of discourse that is built on <math>{X^\bullet}\!</math> is <math>X^{\bullet 2} = [X^\bullet] = [[u, v]],\!</math> which may be developed in the following way. The propositions of <math>{X^\bullet}\!</math> become the points of <math>X^{\bullet 2},\!</math> and the mappings of the type <math>m : (X \to \mathbb{B}) \to \mathbb{B}\!</math> become the propositions of <math>X^{\bullet 2}.\!</math> In addition, it is convenient to equip the discussion with a selected set of higher order operators on propositions, all of which have the form <math>w : (\mathbb{B}^2 \to \mathbb{B})^k \to \mathbb{B}.\!</math> |
| − | To save a few words in the remainder of this discussion, I will use the terms ''measure'' and ''qualifier'' to refer to all types of higher order propositions and operators. To describe the present setting in picturesque terms, the propositions of <math>[u, v]\!</math> may be regarded as a gallery of sixteen venn diagrams, while the measures <math>m : (X \to \mathbb{B}) \to \mathbb{B}</math> are analogous to a body of judges or a panel of critical viewers, each of whom evaluates each of the pictures as a whole and reports the ones that find favor or not. In this way, each judge <math>m_j\!</math> partitions the gallery of pictures into two aesthetic portions, the pictures <math>m_j^{-1}(1)\!</math> that <math>m_j\!</math> likes and the pictures <math>m_j^{-1}(0)\!</math> that <math>m_j\!</math> dislikes. | + | To save a few words in the remainder of this discussion, I will use the terms ''measure'' and ''qualifier'' to refer to all types of higher order propositions and operators. To describe the present setting in picturesque terms, the propositions of <math>[u, v]\!</math> may be regarded as a gallery of sixteen venn diagrams, while the measures <math>m : (X \to \mathbb{B}) \to \mathbb{B}\!</math> are analogous to a body of judges or a panel of critical viewers, each of whom evaluates each of the pictures as a whole and reports the ones that find favor or not. In this way, each judge <math>m_j\!</math> partitions the gallery of pictures into two aesthetic portions, the pictures <math>m_j^{-1}(1)\!</math> that <math>m_j\!</math> likes and the pictures <math>m_j^{-1}(0)\!</math> that <math>m_j\!</math> dislikes. |
| − | There are <math>2^{16} = 65536\!</math> measures of the type <math>m : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}.</math> Table | + | There are <math>2^{16} = 65536\!</math> measures of the type <math>m : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}.\!</math> Table 13 introduces the first 24 of these measures in the fashion of the higher order truth table that I used before. The column headed <math>m_j\!</math> shows the values of the measure <math>m_j\!</math> on each of the propositions <math>f_i : \mathbb{B}^2 \to \mathbb{B},\!</math> for <math>i\!</math> = 0 to 23, with blank entries in the Table being optional for values of zero. The arrangement of measures that continues according to the plan indicated here is referred to as the ''standard ordering'' of these measures. In this scheme of things, the index <math>j\!</math> of the measure <math>m_j\!</math> is the decimal equivalent of the bit string that is associated with <math>m_j\!</math>'s functional values, which can be obtained in turn by reading the <math>j^\mathrm{th}\!</math> column of binary digits in the Table as the corresponding range of boolean values, taking them up in the order from bottom to top. |
| + | |||
| + | <br> | ||
{| align="center" style="background:white; color:black; text-align:center; width:90%" | {| align="center" style="background:white; color:black; text-align:center; width:90%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 13. Higher Order Propositions} ~~ (n = 2)\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| align="right" | <math>\begin{matrix}u\!:\\v\!:\end{matrix}</math> | | align="right" | <math>\begin{matrix}u\!:\\v\!:\end{matrix}</math> | ||
| <math>\begin{matrix}1100\\1010\end{matrix}</math> | | <math>\begin{matrix}1100\\1010\end{matrix}</math> | ||
| <math>f\!</math> | | <math>f\!</math> | ||
| − | | <math>\underset{0}{m}</math> | + | | <math>{\underset{0}{m}}\!</math> |
| − | | <math>\underset{1}{m}</math> | + | | <math>{\underset{1}{m}}\!</math> |
| − | | <math>\underset{2}{m}</math> | + | | <math>{\underset{2}{m}}\!</math> |
| − | | <math>\underset{3}{m}</math> | + | | <math>{\underset{3}{m}}\!</math> |
| − | | <math>\underset{4}{m}</math> | + | | <math>{\underset{4}{m}}\!</math> |
| − | | <math>\underset{5}{m}</math> | + | | <math>{\underset{5}{m}}\!</math> |
| − | | <math>\underset{6}{m}</math> | + | | <math>{\underset{6}{m}}\!</math> |
| − | | <math>\underset{7}{m}</math> | + | | <math>{\underset{7}{m}}\!</math> |
| − | | <math>\underset{8}{m}</math> | + | | <math>{\underset{8}{m}}\!</math> |
| − | | <math>\underset{9}{m}</math> | + | | <math>{\underset{9}{m}}\!</math> |
| − | | <math>\underset{10}{m}</math> | + | | <math>{\underset{10}{m}}\!</math> |
| − | | <math>\underset{11}{m}</math> | + | | <math>{\underset{11}{m}}\!</math> |
| − | | <math>\underset{12}{m}</math> | + | | <math>{\underset{12}{m}}\!</math> |
| − | | <math>\underset{13}{m}</math> | + | | <math>{\underset{13}{m}}\!</math> |
| − | | <math>\underset{14}{m}</math> | + | | <math>{\underset{14}{m}}\!</math> |
| − | | <math>\underset{15}{m}</math> | + | | <math>{\underset{15}{m}}\!</math> |
| − | | <math>\underset{16}{m}</math> | + | | <math>{\underset{16}{m}}\!</math> |
| − | | <math>\underset{17}{m}</math> | + | | <math>{\underset{17}{m}}\!</math> |
| − | | <math>\underset{18}{m}</math> | + | | <math>{\underset{18}{m}}\!</math> |
| − | | <math>\underset{19}{m}</math> | + | | <math>{\underset{19}{m}}\!</math> |
| − | | <math>\underset{20}{m}</math> | + | | <math>{\underset{20}{m}}\!</math> |
| − | | <math>\underset{21}{m}</math> | + | | <math>{\underset{21}{m}}\!</math> |
| − | | <math>\underset{22}{m}</math> | + | | <math>{\underset{22}{m}}\!</math> |
| − | | <math>\underset{23}{m}</math> | + | | <math>{\underset{23}{m}}\!</math> |
|- | |- | ||
| − | | <math>f_0</math> | + | | <math>f_0\!</math> |
| − | | <math>0000</math> | + | | <math>0000\!</math> |
| − | | <math>\texttt{(~)}</math> | + | | <math>\texttt{(~)}\!</math> |
| 0 || style="background:black; color:white" | 1 | | 0 || style="background:black; color:white" | 1 | ||
| 0 || style="background:black; color:white" | 1 | | 0 || style="background:black; color:white" | 1 | ||
| Line 748: | Line 786: | ||
| 0 || style="background:black; color:white" | 1 | | 0 || style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_1</math> | + | | <math>f_1\!</math> |
| − | | <math>0001</math> | + | | <math>0001\!</math> |
| − | | <math>\texttt{(u)(v)}</math> | + | | <math>\texttt{(u)(v)}\!</math> |
| 0 || 0 | | 0 || 0 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 770: | Line 808: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_2</math> | + | | <math>f_2\!</math> |
| − | | <math>0010</math> | + | | <math>{0010}\!</math> |
| − | | <math>\texttt{(u) v}</math> | + | | <math>\texttt{(u) v}\!</math> |
| 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 789: | Line 827: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_3</math> | + | | <math>f_3\!</math> |
| − | | <math>0011</math> | + | | <math>0011\!</math> |
| − | | <math>\texttt{(u)}</math> | + | | <math>\texttt{(u)}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 803: | Line 841: | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_4</math> | + | | <math>f_4\!</math> |
| − | | <math>0100</math> | + | | <math>0100\!</math> |
| − | | <math>\texttt{u (v)}</math> | + | | <math>\texttt{u (v)}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| Line 817: | Line 855: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_5</math> | + | | <math>f_5\!</math> |
| − | | <math>0101</math> | + | | <math>{0101}\!</math> |
| − | | <math>\texttt{(v)}</math> | + | | <math>\texttt{(v)}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_6</math> | + | | <math>f_6\!</math> |
| − | | <math>0110</math> | + | | <math>0110\!</math> |
| − | | <math>\texttt{(u, v)}</math> | + | | <math>\texttt{(u, v)}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_7</math> | + | | <math>f_7\!</math> |
| − | | <math>0111</math> | + | | <math>0111\!</math> |
| − | | <math>\texttt{(u v)}</math> | + | | <math>\texttt{(u v)}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_8</math> | + | | <math>f_8\!</math> |
| − | | <math>1000</math> | + | | <math>1000\!</math> |
| − | | <math>\texttt{u v}</math> | + | | <math>\texttt{u v}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_9</math> | + | | <math>f_9\!</math> |
| − | | <math>1001</math> | + | | <math>1001\!</math> |
| − | | <math>\texttt{((u, v))}</math> | + | | <math>\texttt{((u, v))}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_{10}</math> | + | | <math>f_{10}\!</math> |
| − | | <math>1010</math> | + | | <math>1010\!</math> |
| − | | <math>\texttt{v}</math> | + | | <math>\texttt{v}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_{11}</math> | + | | <math>f_{11}\!</math> |
| − | | <math>1011</math> | + | | <math>1011\!</math> |
| − | | <math>\texttt{(u (v))}</math> | + | | <math>\texttt{(u (v))}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_{12}</math> | + | | <math>f_{12}\!</math> |
| − | | <math>1100</math> | + | | <math>1100\!</math> |
| − | | <math>\texttt{u}</math> | + | | <math>\texttt{u}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_{13}</math> | + | | <math>f_{13}\!</math> |
| − | | <math>1101</math> | + | | <math>1101\!</math> |
| − | | <math>\texttt{((u) v)}</math> | + | | <math>\texttt{((u) v)}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_{14}</math> | + | | <math>f_{14}\!</math> |
| − | | <math>1110</math> | + | | <math>1110\!</math> |
| − | | <math>\texttt{((u)(v))}</math> | + | | <math>\texttt{((u)(v))}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
|- | |- | ||
| − | | <math>f_{15}</math> | + | | <math>f_{15}\!</math> |
| − | | <math>1111</math> | + | | <math>1111\!</math> |
| − | | <math>\texttt{((~))}</math> | + | | <math>\texttt{((~))}\!</math> |
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | | 0 || 0 || 0 || 0 || 0 || 0 || 0 || 0 | ||
| Line 899: | Line 937: | ||
===Umpire Operators=== | ===Umpire Operators=== | ||
| − | We now examine measures at the high end of the standard ordering. Instrumental to this purpose we define a couple of higher order operators, <math>\Upsilon_1 : (\langle u, v \rangle \to \mathbb{B}) \to \mathbb{B}</math> and <math>\Upsilon : (\langle u, v \rangle \to \mathbb{B})^2 \to \mathbb{B},</math> both symbolized by cursive upsilon characters and referred to as the absolute and relative ''umpire operators'', respectively. If either one of these operators is defined in terms of more primitive notions then the remaining operator can be defined in terms of the one first established. | + | We now examine measures at the high end of the standard ordering. Instrumental to this purpose we define a couple of higher order operators, <math>\Upsilon_1 : (\langle u, v \rangle \to \mathbb{B}) \to \mathbb{B}\!</math> and <math>\Upsilon : (\langle u, v \rangle \to \mathbb{B})^2 \to \mathbb{B},\!</math> both symbolized by cursive upsilon characters and referred to as the absolute and relative ''umpire operators'', respectively. If either one of these operators is defined in terms of more primitive notions then the remaining operator can be defined in terms of the one first established. |
| − | Given an ordered pair of propositions <math>e, f : \langle u, v \rangle \to \mathbb{B}</math> as arguments, the relative operator reports the value <math>1\!</math> if the first implies the second, otherwise <math>0.\!</math> | + | Given an ordered pair of propositions <math>e, f : \langle u, v \rangle \to \mathbb{B}\!</math> as arguments, the relative operator reports the value <math>1\!</math> if the first implies the second, otherwise <math>0.\!</math> |
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| <math>\Upsilon (e, f) = 1\!</math> | | <math>\Upsilon (e, f) = 1\!</math> | ||
| − | | <math>\operatorname{if~and~only~if}</math> | + | | <math>\operatorname{if~and~only~if}\!</math> |
| <math>e \Rightarrow f.\!</math> | | <math>e \Rightarrow f.\!</math> | ||
|} | |} | ||
| Line 913: | Line 951: | ||
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| <math>\Upsilon (e, f) = 1\!</math> | | <math>\Upsilon (e, f) = 1\!</math> | ||
| − | | <math>\iff</math> | + | | <math>\iff\!</math> |
| − | | <math>\texttt{(} e \texttt{(} f \texttt{))} = 1</math> | + | | <math>\texttt{(} e \texttt{(} f \texttt{))} = 1\!</math> |
|} | |} | ||
| Line 920: | Line 958: | ||
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| − | | <math>\Upsilon (e, f) = 1 \in \mathbb{B}</math> | + | | <math>\Upsilon (e, f) = 1 \in \mathbb{B}\!</math> |
| − | | <math>\iff</math> | + | | <math>\iff\!</math> |
| − | | <math>\texttt{(} e \texttt{(} f \texttt{))} = 1 : \langle u, v \rangle \to \mathbb{B}</math> | + | | <math>\texttt{(} e \texttt{(} f \texttt{))} = 1 : \langle u, v \rangle \to \mathbb{B}\!</math> |
|} | |} | ||
| − | Writing types as subscripts and using the fact that <math>X = \langle u, v \rangle,</math> it is possible to express this a little more succinctly as follows: | + | Writing types as subscripts and using the fact that <math>X = \langle u, v \rangle,\!</math> it is possible to express this a little more succinctly as follows: |
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| − | | <math>\Upsilon (e, f) = 1_\mathbb{B}</math> | + | | <math>\Upsilon (e, f) = 1_\mathbb{B}\!</math> |
| − | | <math>\iff</math> | + | | <math>\iff\!</math> |
| − | | <math>\texttt{(} e \texttt{(} f \texttt{))} = 1_{X \to \mathbb{B}}</math> | + | | <math>\texttt{(} e \texttt{(} f \texttt{))} = 1_{X \to \mathbb{B}}\!</math> |
|} | |} | ||
Finally, it is often convenient to write the first argument as a subscript, hence <math>\Upsilon_e (f) = \Upsilon (e, f).\!</math> | Finally, it is often convenient to write the first argument as a subscript, hence <math>\Upsilon_e (f) = \Upsilon (e, f).\!</math> | ||
| − | As a special application of this operator, we next define the absolute umpire operator, also called the ''umpire measure''. This is a higher order proposition <math>\Upsilon_1 : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}</math> which is given by the relation <math>\Upsilon_1 (f) = \Upsilon (1, f).\!</math> Here, the subscript <math>1\!</math> on the left and the argument <math>1\!</math> on the right both refer to the constant proposition <math>1 : \mathbb{B}^2 \to \mathbb{B}.</math> In most contexts where <math>\Upsilon_1\!</math> is actually applied the subscript <math>1\!</math> is safely omitted, since the number of arguments indicates which type of operator is intended. Thus, we have the following identities and equivalents: | + | As a special application of this operator, we next define the absolute umpire operator, also called the ''umpire measure''. This is a higher order proposition <math>\Upsilon_1 : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}\!</math> which is given by the relation <math>\Upsilon_1 (f) = \Upsilon (1, f).\!</math> Here, the subscript <math>1\!</math> on the left and the argument <math>1\!</math> on the right both refer to the constant proposition <math>1 : \mathbb{B}^2 \to \mathbb{B}.\!</math> In most contexts where <math>\Upsilon_1\!</math> is actually applied the subscript <math>1\!</math> is safely omitted, since the number of arguments indicates which type of operator is intended. Thus, we have the following identities and equivalents: |
{| align="center" cellpadding="10" style="text-align:center" | {| align="center" cellpadding="10" style="text-align:center" | ||
| − | | <math>\Upsilon f = \Upsilon_1 (f) = 1 \in \mathbb{B}</math> | + | | <math>\Upsilon f = \Upsilon_1 (f) = 1 \in \mathbb{B}\!</math> |
| − | | <math>\iff</math> | + | | <math>\iff\!</math> |
| − | | <math>\texttt{(} 1 ~ \texttt{(} f \texttt{))} = 1</math> | + | | <math>\texttt{(} 1 ~ \texttt{(} f \texttt{))} = 1\!</math> |
| − | | <math>\iff</math> | + | | <math>\iff\!</math> |
| − | | <math>f = 1 : \mathbb{B}^2 \to \mathbb{B}</math> | + | | <math>f = 1 : \mathbb{B}^2 \to \mathbb{B}\!</math> |
|} | |} | ||
The umpire measure is defined at the level of truth functions, but can also be understood in terms of its implied judgments at the syntactic level. Interpreted this way, <math>\Upsilon_1\!</math> recognizes theorems of the propositional calculus over <math>[u, v],\!</math> giving a score of <math>1\!</math> to tautologies and a score of <math>0\!</math> to everything else, regarding all contingent statements as no better than falsehoods. | The umpire measure is defined at the level of truth functions, but can also be understood in terms of its implied judgments at the syntactic level. Interpreted this way, <math>\Upsilon_1\!</math> recognizes theorems of the propositional calculus over <math>[u, v],\!</math> giving a score of <math>1\!</math> to tautologies and a score of <math>0\!</math> to everything else, regarding all contingent statements as no better than falsehoods. | ||
| − | One remark in passing for those who might prefer an alternative definition. If we had originally taken <math>\Upsilon\!</math> to mean the absolute measure, then the relative version could have been defined as <math>\Upsilon_e f = \Upsilon \texttt{(} e \texttt{(} f \texttt{))}.</math> | + | One remark in passing for those who might prefer an alternative definition. If we had originally taken <math>\Upsilon\!</math> to mean the absolute measure, then the relative version could have been defined as <math>\Upsilon_e f = \Upsilon \texttt{(} e \texttt{(} f \texttt{))}.~\!</math> |
===Measure for Measure=== | ===Measure for Measure=== | ||
| Line 954: | Line 992: | ||
{| align="center" cellpadding="8" | {| align="center" cellpadding="8" | ||
| − | | <math>\alpha_i, \beta_i : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}, i = 0 \ldots 15,</math> | + | | <math>\alpha_i, \beta_i : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}, i = 0 \ldots 15,\!</math> |
|} | |} | ||
| Line 960: | Line 998: | ||
{| align="center" cellpadding="8" | {| align="center" cellpadding="8" | ||
| − | | <math>\alpha_i f = \Upsilon (f_i, f) = \Upsilon (f_i \Rightarrow f),</math> | + | | <math>\alpha_i f = \Upsilon (f_i, f) = \Upsilon (f_i \Rightarrow f),\!</math> |
|- | |- | ||
| − | | <math>\beta_i f = \Upsilon (f, f_i) = \Upsilon (f \Rightarrow f_i).</math> | + | | <math>\beta_i f = \Upsilon (f, f_i) = \Upsilon (f \Rightarrow f_i).\!</math> |
|} | |} | ||
| − | The values of the sixteen <math>\alpha_i\!</math> on each of the sixteen boolean functions <math>f : \mathbb{B}^2 \to \mathbb{B}</math> are shown in Table | + | <br> |
| + | |||
| + | The values of the sixteen <math>\alpha_i\!</math> on each of the sixteen boolean functions <math>f : \mathbb{B}^2 \to \mathbb{B}\!</math> are shown in Table 14. Expressed in terms of the implication ordering on the sixteen functions, <math>\alpha_i f = 1\!</math> says that <math>f\!</math> is ''above or identical to'' <math>f_i\!</math> in the implication lattice, that is, <math>\ge f_i\!</math> in the implication ordering. | ||
| + | |||
| + | <br> | ||
{| align="center" border="1" cellpadding="1" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | {| align="center" border="1" cellpadding="1" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 14. Qualifiers of Implication Ordering:} ~~ \alpha_i f = \Upsilon (f_i, f) = \Upsilon (f_i \Rightarrow f)\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| − | | align="right" | <math>u:</math><br><math>v:</math> | + | | align="right" | <math>u:\!</math><br><math>v:\!</math> |
| 1100<br>1010 | | 1100<br>1010 | ||
| <math>f\!</math> | | <math>f\!</math> | ||
| − | | <math>\alpha_0</math> | + | | <math>\alpha_0~\!</math> |
| − | | <math>\alpha_1</math> | + | | <math>\alpha_1\!</math> |
| − | | <math>\alpha_2</math> | + | | <math>\alpha_2\!</math> |
| − | | <math>\alpha_3</math> | + | | <math>\alpha_3\!</math> |
| − | | <math>\alpha_4</math> | + | | <math>\alpha_4\!</math> |
| − | | <math>\alpha_5</math> | + | | <math>\alpha_5\!</math> |
| − | | <math>\alpha_6</math> | + | | <math>\alpha_6\!</math> |
| − | | <math>\alpha_7</math> | + | | <math>\alpha_7\!</math> |
| − | | <math>\alpha_8</math> | + | | <math>\alpha_8\!</math> |
| − | | <math>\alpha_9</math> | + | | <math>\alpha_9\!</math> |
| − | | <math>\alpha_{10}</math> | + | | <math>\alpha_{10}\!</math> |
| − | | <math>\alpha_{11}</math> | + | | <math>\alpha_{11}\!</math> |
| − | | <math>\alpha_{12}</math> | + | | <math>\alpha_{12}\!</math> |
| − | | <math>\alpha_{13}</math> | + | | <math>\alpha_{13}~\!</math> |
| − | | <math>\alpha_{14}</math> | + | | <math>\alpha_{14}\!</math> |
| − | | <math>\alpha_{15}</math> | + | | <math>\alpha_{15}\!</math> |
|- | |- | ||
| − | | <math>f_0</math> | + | | <math>f_0\!</math> |
| 0000 | | 0000 | ||
| − | | <math>\texttt{(~)}</math> | + | | <math>\texttt{(~)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,010: | Line 1,053: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_1</math> | + | | <math>f_1\!</math> |
| 0001 | | 0001 | ||
| − | | <math>\texttt{(} u \texttt{)(} v \texttt{)}</math> | + | | <math>\texttt{(} u \texttt{)(} v \texttt{)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,030: | Line 1,073: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_2</math> | + | | <math>f_2\!</math> |
| 0010 | | 0010 | ||
| − | | <math>\texttt{(} u \texttt{)} ~ v</math> | + | | <math>\texttt{(} u \texttt{)} ~ v\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,050: | Line 1,093: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_3</math> | + | | <math>f_3\!</math> |
| 0011 | | 0011 | ||
| − | | <math>\texttt{(} u \texttt{)}</math> | + | | <math>\texttt{(} u \texttt{)}~\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,070: | Line 1,113: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_4</math> | + | | <math>f_4\!</math> |
| 0100 | | 0100 | ||
| − | | <math>u ~ \texttt{(} v \texttt{)}</math> | + | | <math>u ~ \texttt{(} v \texttt{)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,090: | Line 1,133: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_5</math> | + | | <math>f_5\!</math> |
| 0101 | | 0101 | ||
| − | | <math>\texttt{(} v \texttt{)}</math> | + | | <math>\texttt{(} v \texttt{)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,110: | Line 1,153: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_6</math> | + | | <math>f_6\!</math> |
| 0110 | | 0110 | ||
| − | | <math>\texttt{(} u ~ \texttt{,} ~ v \texttt{)}</math> | + | | <math>\texttt{(} u ~ \texttt{,} ~ v \texttt{)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,130: | Line 1,173: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_7</math> | + | | <math>f_7\!</math> |
| 0111 | | 0111 | ||
| − | | <math>\texttt{(} u ~ v \texttt{)}</math> | + | | <math>\texttt{(} u ~ v \texttt{)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,150: | Line 1,193: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_8</math> | + | | <math>f_8\!</math> |
| 1000 | | 1000 | ||
| − | | <math>u ~ v</math> | + | | <math>u ~ v\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,170: | Line 1,213: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_9</math> | + | | <math>f_9\!</math> |
| 1001 | | 1001 | ||
| − | | <math>\texttt{((} u ~ \texttt{,} ~ v \texttt{))}</math> | + | | <math>\texttt{((} u ~ \texttt{,} ~ v \texttt{))}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,190: | Line 1,233: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{10}</math> | + | | <math>f_{10}\!</math> |
| 1010 | | 1010 | ||
| <math>v\!</math> | | <math>v\!</math> | ||
| Line 1,210: | Line 1,253: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{11}</math> | + | | <math>f_{11}\!</math> |
| 1011 | | 1011 | ||
| − | | <math>\texttt{(} u ~ \texttt{(} v \texttt{))}</math> | + | | <math>\texttt{(} u ~ \texttt{(} v \texttt{))}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,230: | Line 1,273: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{12}</math> | + | | <math>f_{12}\!</math> |
| 1100 | | 1100 | ||
| <math>u\!</math> | | <math>u\!</math> | ||
| Line 1,250: | Line 1,293: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{13}</math> | + | | <math>f_{13}\!</math> |
| 1101 | | 1101 | ||
| − | | <math>\texttt{((} u \texttt{)} ~ v \texttt{)}</math> | + | | <math>\texttt{((} u \texttt{)} ~ v \texttt{)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,270: | Line 1,313: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{14}</math> | + | | <math>f_{14}\!</math> |
| 1110 | | 1110 | ||
| − | | <math>\texttt{((} u \texttt{)(} v \texttt{))}</math> | + | | <math>\texttt{((} u \texttt{)(} v \texttt{))}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,290: | Line 1,333: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{15}</math> | + | | <math>f_{15}\!</math> |
| 1111 | | 1111 | ||
| − | | <math>\texttt{((~))}</math> | + | | <math>\texttt{((~))}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,309: | Line 1,352: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| − | |}<br> | + | |} |
| + | |||
| + | <br> | ||
| + | |||
| + | The values of the sixteen <math>{\beta_i}\!</math> on each of the sixteen boolean functions <math>{f : \mathbb{B}^2 \to \mathbb{B}}\!</math> are shown in Table 15. Expressed in terms of the implication ordering on the sixteen functions, <math>{\beta_i f = 1}\!</math> says that <math>{f}\!</math> is ''below or identical to'' <math>{f_i}\!</math> in the implication lattice, that is, <math>{\le f_i}\!</math> in the implication ordering. | ||
| − | + | <br> | |
{| align="center" border="1" cellpadding="1" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | {| align="center" border="1" cellpadding="1" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 15. Qualifiers of Implication Ordering:} ~~ \beta_i f = \Upsilon (f, f_i) = \Upsilon (f \Rightarrow f_i)\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| − | | align="right" | <math>u:</math><br><math>v:</math> | + | | align="right" | <math>u:\!</math><br><math>v:\!</math> |
| 1100<br>1010 | | 1100<br>1010 | ||
| <math>f\!</math> | | <math>f\!</math> | ||
| − | | <math>\beta_0</math> | + | | <math>\beta_0\!</math> |
| − | | <math>\beta_1</math> | + | | <math>\beta_1\!</math> |
| − | | <math>\beta_2</math> | + | | <math>\beta_2\!</math> |
| − | | <math>\beta_3</math> | + | | <math>\beta_3\!</math> |
| − | | <math>\beta_4</math> | + | | <math>\beta_4\!</math> |
| − | | <math>\beta_5</math> | + | | <math>\beta_5\!</math> |
| − | | <math>\beta_6</math> | + | | <math>\beta_6\!</math> |
| − | | <math>\beta_7</math> | + | | <math>\beta_7\!</math> |
| − | | <math>\beta_8</math> | + | | <math>\beta_8\!</math> |
| − | | <math>\beta_9</math> | + | | <math>\beta_9\!</math> |
| − | | <math>\beta_{10}</math> | + | | <math>\beta_{10}\!</math> |
| − | | <math>\beta_{11}</math> | + | | <math>\beta_{11}\!</math> |
| − | | <math>\beta_{12}</math> | + | | <math>\beta_{12}\!</math> |
| − | | <math>\beta_{13}</math> | + | | <math>\beta_{13}\!</math> |
| − | | <math>\beta_{14}</math> | + | | <math>\beta_{14}\!</math> |
| − | | <math>\beta_{15}</math> | + | | <math>\beta_{15}\!</math> |
|- | |- | ||
| − | | <math>f_0</math> | + | | <math>f_0\!</math> |
| 0000 | | 0000 | ||
| − | | <math>\texttt{(~)}</math> | + | | <math>\texttt{(~)}\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,356: | Line 1,404: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_1</math> | + | | <math>f_1\!</math> |
| 0001 | | 0001 | ||
| − | | <math>\texttt{(} u \texttt{)(} v \texttt{)}</math> | + | | <math>\texttt{(} u \texttt{)(} v \texttt{)}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,376: | Line 1,424: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_2</math> | + | | <math>f_2\!</math> |
| 0010 | | 0010 | ||
| − | | <math>\texttt{(} u \texttt{)} ~ v</math> | + | | <math>\texttt{(} u \texttt{)} ~ v\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,396: | Line 1,444: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_3</math> | + | | <math>f_3\!</math> |
| 0011 | | 0011 | ||
| − | | <math>\texttt{(} u \texttt{)}</math> | + | | <math>\texttt{(} u \texttt{)}~\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,416: | Line 1,464: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_4</math> | + | | <math>f_4\!</math> |
| 0100 | | 0100 | ||
| − | | <math>u ~ \texttt{(} v \texttt{)}</math> | + | | <math>u ~ \texttt{(} v \texttt{)}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,436: | Line 1,484: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_5</math> | + | | <math>f_5\!</math> |
| 0101 | | 0101 | ||
| − | | <math>\texttt{(} v \texttt{)}</math> | + | | <math>\texttt{(} v \texttt{)}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,456: | Line 1,504: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_6</math> | + | | <math>f_6\!</math> |
| 0110 | | 0110 | ||
| − | | <math>\texttt{(} u ~ \texttt{,} ~ v \texttt{)}</math> | + | | <math>\texttt{(} u ~ \texttt{,} ~ v \texttt{)}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,476: | Line 1,524: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_7</math> | + | | <math>f_7\!</math> |
| 0111 | | 0111 | ||
| − | | <math>\texttt{(} u ~ v \texttt{)}</math> | + | | <math>\texttt{(} u ~ v \texttt{)}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,496: | Line 1,544: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_8</math> | + | | <math>f_8\!</math> |
| 1000 | | 1000 | ||
| − | | <math>u ~ v</math> | + | | <math>u ~ v\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,516: | Line 1,564: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_9</math> | + | | <math>f_9\!</math> |
| 1001 | | 1001 | ||
| − | | <math>\texttt{((} u ~ \texttt{,} ~ v \texttt{))}</math> | + | | <math>\texttt{((} u ~ \texttt{,} ~ v \texttt{))}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,536: | Line 1,584: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{10}</math> | + | | <math>f_{10}\!</math> |
| 1010 | | 1010 | ||
| <math>v\!</math> | | <math>v\!</math> | ||
| Line 1,556: | Line 1,604: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{11}</math> | + | | <math>f_{11}\!</math> |
| 1011 | | 1011 | ||
| − | | <math>\texttt{(} u ~ \texttt{(} v \texttt{))}</math> | + | | <math>\texttt{(} u ~ \texttt{(} v \texttt{))}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,576: | Line 1,624: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{12}</math> | + | | <math>f_{12}\!</math> |
| 1100 | | 1100 | ||
| <math>u\!</math> | | <math>u\!</math> | ||
| Line 1,596: | Line 1,644: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{13}</math> | + | | <math>f_{13}\!</math> |
| 1101 | | 1101 | ||
| − | | <math>\texttt{((} u \texttt{)} ~ v \texttt{)}</math> | + | | <math>\texttt{((} u \texttt{)} ~ v \texttt{)}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,616: | Line 1,664: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{14}</math> | + | | <math>f_{14}\!</math> |
| 1110 | | 1110 | ||
| − | | <math>\texttt{((} u \texttt{)(} v \texttt{))}</math> | + | | <math>\texttt{((} u \texttt{)(} v \texttt{))}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,636: | Line 1,684: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{15}</math> | + | | <math>f_{15}\!</math> |
| 1111 | | 1111 | ||
| − | | <math>\texttt{((~))}</math> | + | | <math>\texttt{((~))}\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,655: | Line 1,703: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| − | |}<br> | + | |} |
| + | |||
| + | <br> | ||
| − | Applied to a given proposition <math>f,\!</math> the qualifiers <math>\alpha_i\!</math> and <math>\beta_i\!</math> tell whether <math>f\!</math> rests <math>\operatorname{above}\ f_i</math> or <math>\operatorname{below}\ f_i,</math> respectively, in the implication ordering. By way of example, let us trace the effects of several such measures, namely, those that occupy the limiting positions of the Tables. | + | Applied to a given proposition <math>f,\!</math> the qualifiers <math>\alpha_i\!</math> and <math>\beta_i\!</math> tell whether <math>f\!</math> rests <math>\operatorname{above}\ f_i\!</math> or <math>\operatorname{below}\ f_i,\!</math> respectively, in the implication ordering. By way of example, let us trace the effects of several such measures, namely, those that occupy the limiting positions of the Tables. |
{| align="center" cellpadding="8" | {| align="center" cellpadding="8" | ||
| Line 1,700: | Line 1,750: | ||
|} | |} | ||
| − | Thus, <math>\alpha_0 = \beta_{15}\!</math> is a totally indiscriminate measure, one that accepts all propositions <math>f : \mathbb{B}^2 \to \mathbb{B},</math> whereas <math>\alpha_{15}\!</math> and <math>\beta_0\!</math> are measures that value the constant propositions <math>1 : \mathbb{B}^2 \to \mathbb{B}</math> and <math>0 : \mathbb{B}^2 \to \mathbb{B},</math> respectively, above all others. | + | Thus, <math>\alpha_0 = \beta_{15}\!</math> is a totally indiscriminate measure, one that accepts all propositions <math>{f : \mathbb{B}^2 \to \mathbb{B}},\!</math> whereas <math>\alpha_{15}\!</math> and <math>\beta_0\!</math> are measures that value the constant propositions <math>1 : \mathbb{B}^2 \to \mathbb{B}\!</math> and <math>0 : \mathbb{B}^2 \to \mathbb{B},\!</math> respectively, above all others. |
Finally, in conformity with the use of the fiber notation to indicate sets of models, it is natural to use notations like: | Finally, in conformity with the use of the fiber notation to indicate sets of models, it is natural to use notations like: | ||
| Line 1,724: | Line 1,774: | ||
Previously I introduced a calculus for propositional logic, fixing its meaning according to what C.S. Peirce called the ''existential interpretation''. As far as it concerns propositional calculus this interpretation settles the meanings that are associated with merely the most basic symbols and logical connectives. Now we must extend and refine the existential interpretation to comprehend the analysis of ''quantifications'', that is, quantified propositions. In doing so we recognize two additional aspects of logic that need to be developed, over and above the material of propositional logic. At the formal extreme there is the aspect of higher order functional types, into which we have already ventured a little above. At the level of the fundamental content of the available propositions we have to introduce a different interpretation for what we may call ''elemental'' or ''singular'' propositions. | Previously I introduced a calculus for propositional logic, fixing its meaning according to what C.S. Peirce called the ''existential interpretation''. As far as it concerns propositional calculus this interpretation settles the meanings that are associated with merely the most basic symbols and logical connectives. Now we must extend and refine the existential interpretation to comprehend the analysis of ''quantifications'', that is, quantified propositions. In doing so we recognize two additional aspects of logic that need to be developed, over and above the material of propositional logic. At the formal extreme there is the aspect of higher order functional types, into which we have already ventured a little above. At the level of the fundamental content of the available propositions we have to introduce a different interpretation for what we may call ''elemental'' or ''singular'' propositions. | ||
| − | Let us return to the 2-dimensional case <math>X^\ | + | Let us return to the 2-dimensional case <math>X^\bullet = [u, v].\!</math> In order to provide a bridge between propositions and quantifications it serves to define a set of qualifiers <math>\ell_{ij} : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}\!</math> that have the following characters: |
<center><math>\begin{array}{llllll} | <center><math>\begin{array}{llllll} | ||
| Line 1,753: | Line 1,803: | ||
\end{array}</math></center> | \end{array}</math></center> | ||
| − | Intuitively, the <math>\ell_{ij}\!</math> operators may be thought of as qualifying propositions according to the elements of the universe of discourse that each proposition positively values. Taken together, these measures provide us with the means to express many useful observations about the propositions in <math>X^\ | + | Intuitively, the <math>\ell_{ij}\!</math> operators may be thought of as qualifying propositions according to the elements of the universe of discourse that each proposition positively values. Taken together, these measures provide us with the means to express many useful observations about the propositions in <math>X^\bullet = [u, v],\!</math> and so they mediate a subtext <math>[\ell_{00}, \ell_{01}, \ell_{10}, \ell_{11}]\!</math> that takes place within the higher order universe of discourse <math>X^{\bullet 2} = [X^\bullet] = [[u, v]].\!</math> Figure 16 summarizes the action of the <math>\ell_{ij}\!</math> operators on the <math>f_i\!</math> within <math>X^{\bullet 2}.\!</math> |
{| align="center" cellpadding="10" style="text-align:center" | {| align="center" cellpadding="10" style="text-align:center" | ||
| − | | [[Image:Venn Diagram 4 Dimensions UV Cacti 8 Inch. | + | | [[Image:Venn Diagram 4 Dimensions UV Cacti 8 Inch.jpg]] |
|- | |- | ||
| − | | <math>\text{Figure | + | | <math>\text{Figure 16.} ~~ \text{Higher Order Universe of Discourse} ~ \left[ \ell_{00}, \ell_{01}, \ell_{10}, \ell_{11} \right] \subseteq \left[\left[ u, v \right]\right]\!</math> |
|} | |} | ||
| Line 1,765: | Line 1,815: | ||
Our excursion into the vastening landscape of higher order propositions has finally come round to the stage where we can bring its returns to bear on opening up new perspectives for quantificational logic. | Our excursion into the vastening landscape of higher order propositions has finally come round to the stage where we can bring its returns to bear on opening up new perspectives for quantificational logic. | ||
| − | There is a question arising next that is still experimental in my mind. Whether it makes much difference from a purely formal point of view is not a question I can answer yet, but it does seem to aid the intuition to invent a slightly different interpretation for the two-valued space that we use as the target of our basic indicator functions. Therefore, let us declare a type of ''existential-valued'' functions <math>f : \mathbb{B}^k \to \mathbb{E},</math> where <math>\mathbb{E} = \{ -e, +e \} = \{ \operatorname{empty}, \operatorname{exist} \}</math> is a couple of values that we interpret as indicating whether of not anything exists in the cells of the underlying universe of discourse, venn diagram, or other domain. As usual, let us not be too strict about the coding of these functions, reverting to binary codes whenever the interpretation is clear enough. | + | There is a question arising next that is still experimental in my mind. Whether it makes much difference from a purely formal point of view is not a question I can answer yet, but it does seem to aid the intuition to invent a slightly different interpretation for the two-valued space that we use as the target of our basic indicator functions. Therefore, let us declare a type of ''existential-valued'' functions <math>f : \mathbb{B}^k \to \mathbb{E},\!</math> where <math>\mathbb{E} = \{ -e, +e \} = \{ \operatorname{empty}, \operatorname{exist} \}\!</math> is a couple of values that we interpret as indicating whether of not anything exists in the cells of the underlying universe of discourse, venn diagram, or other domain. As usual, let us not be too strict about the coding of these functions, reverting to binary codes whenever the interpretation is clear enough. |
With this interpretation in mind we note the following correspondences between classical quantifications and higher order indicator functions: | With this interpretation in mind we note the following correspondences between classical quantifications and higher order indicator functions: | ||
| + | |||
| + | <br> | ||
{| align="center" border="1" cellpadding="8" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | {| align="center" border="1" cellpadding="8" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 17. Syllogistic Premisses as Higher Order Indicator Functions}\!</math> | ||
| | | | ||
<math>\begin{array}{clcl} | <math>\begin{array}{clcl} | ||
| Line 1,790: | Line 1,843: | ||
\mathrm{Indicator~of}\ u (v) = 1 \\ | \mathrm{Indicator~of}\ u (v) = 1 \\ | ||
\end{array}</math> | \end{array}</math> | ||
| − | |}<br> | + | |} |
| + | |||
| + | <br> | ||
The following Tables develop these ideas in more detail. | The following Tables develop these ideas in more detail. | ||
| + | |||
| + | <br> | ||
{| align="center" border="1" cellpadding="2" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | {| align="center" border="1" cellpadding="2" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 18. Simple Qualifiers of Propositions (Version 1)}\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| − | | align="right" | <math>u:</math><br><math>v:</math> | + | | align="right" | <math>u:\!</math><br><math>v:\!</math> |
| 1100<br>1010 | | 1100<br>1010 | ||
| <math>f\!</math> | | <math>f\!</math> | ||
| − | | <math>(\ell_{11})</math><br><math>\text{No } u </math><br><math>\text{is } v </math> | + | | <math>(\ell_{11})\!</math><br><math>\text{No } u \!</math><br><math>\text{is } v \!</math> |
| − | | <math>(\ell_{10})</math><br><math>\text{No } u </math><br><math>\text{is }(v)</math> | + | | <math>(\ell_{10})\!</math><br><math>\text{No } u \!</math><br><math>\text{is }(v)\!</math> |
| − | | <math>(\ell_{01})</math><br><math>\text{No }(u)</math><br><math>\text{is } v </math> | + | | <math>(\ell_{01})\!</math><br><math>\text{No }(u)\!</math><br><math>\text{is } v \!</math> |
| − | | <math>(\ell_{00})</math><br><math>\text{No }(u)</math><br><math>\text{is }(v)</math> | + | | <math>(\ell_{00})\!</math><br><math>\text{No }(u)\!</math><br><math>\text{is }(v)\!</math> |
| − | | <math> \ell_{00} </math><br><math>\text{Some }(u)</math><br><math>\text{is }(v)</math> | + | | <math> \ell_{00} \!</math><br><math>\text{Some }(u)\!</math><br><math>\text{is }(v)\!</math> |
| − | | <math> \ell_{01} </math><br><math>\text{Some }(u)</math><br><math>\text{is } v </math> | + | | <math> \ell_{01} \!</math><br><math>\text{Some }(u)\!</math><br><math>\text{is } v \!</math> |
| − | | <math> \ell_{10} </math><br><math>\text{Some } u </math><br><math>\text{is }(v)</math> | + | | <math> \ell_{10}~\!</math><br><math>\text{Some } u \!</math><br><math>\text{is }(v)\!</math> |
| − | | <math> \ell_{11} </math><br><math>\text{Some } u </math><br><math>\text{is } v </math> | + | | <math> \ell_{11} \!</math><br><math>\text{Some } u \!</math><br><math>\text{is } v \!</math> |
|- | |- | ||
| − | | <math>f_0</math> | + | | <math>f_0\!</math> |
| 0000 | | 0000 | ||
| − | | <math>(~)</math> | + | | <math>(~)\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,821: | Line 1,879: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_1</math> | + | | <math>f_1\!</math> |
| 0001 | | 0001 | ||
| <math>(u)(v)\!</math> | | <math>(u)(v)\!</math> | ||
| Line 1,833: | Line 1,891: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_2</math> | + | | <math>f_2\!</math> |
| 0010 | | 0010 | ||
| <math>(u) v\!</math> | | <math>(u) v\!</math> | ||
| Line 1,845: | Line 1,903: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_3</math> | + | | <math>f_3\!</math> |
| 0011 | | 0011 | ||
| − | | <math>(u)\!</math> | + | | <math>(u)~\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 1,857: | Line 1,915: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_4</math> | + | | <math>f_4\!</math> |
| 0100 | | 0100 | ||
| <math>u (v)\!</math> | | <math>u (v)\!</math> | ||
| Line 1,869: | Line 1,927: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_5</math> | + | | <math>f_5\!</math> |
| 0101 | | 0101 | ||
| <math>(v)\!</math> | | <math>(v)\!</math> | ||
| Line 1,881: | Line 1,939: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_6</math> | + | | <math>f_6\!</math> |
| 0110 | | 0110 | ||
| <math>(u, v)\!</math> | | <math>(u, v)\!</math> | ||
| Line 1,893: | Line 1,951: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_7</math> | + | | <math>f_7\!</math> |
| 0111 | | 0111 | ||
| <math>(u v)\!</math> | | <math>(u v)\!</math> | ||
| Line 1,905: | Line 1,963: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_8</math> | + | | <math>f_8\!</math> |
| 1000 | | 1000 | ||
| <math>u v\!</math> | | <math>u v\!</math> | ||
| Line 1,917: | Line 1,975: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_9</math> | + | | <math>f_9\!</math> |
| 1001 | | 1001 | ||
| <math>((u, v))\!</math> | | <math>((u, v))\!</math> | ||
| Line 1,929: | Line 1,987: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{10}</math> | + | | <math>f_{10}\!</math> |
| 1010 | | 1010 | ||
| <math>v\!</math> | | <math>v\!</math> | ||
| Line 1,941: | Line 1,999: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{11}</math> | + | | <math>f_{11}\!</math> |
| 1011 | | 1011 | ||
| <math>(u (v))\!</math> | | <math>(u (v))\!</math> | ||
| Line 1,953: | Line 2,011: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{12}</math> | + | | <math>f_{12}\!</math> |
| 1100 | | 1100 | ||
| <math>u\!</math> | | <math>u\!</math> | ||
| Line 1,965: | Line 2,023: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{13}</math> | + | | <math>f_{13}\!</math> |
| 1101 | | 1101 | ||
| <math>((u) v)\!</math> | | <math>((u) v)\!</math> | ||
| Line 1,977: | Line 2,035: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{14}</math> | + | | <math>f_{14}\!</math> |
| 1110 | | 1110 | ||
| − | | <math>((u)(v))\!</math> | + | | <math>((u)(v))~\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 1,989: | Line 2,047: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{15}</math> | + | | <math>f_{15}\!</math> |
| 1111 | | 1111 | ||
| − | | <math>((~))</math> | + | | <math>((~))\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 2,000: | Line 2,058: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| − | |}<br> | + | |} |
| + | |||
| + | <br> | ||
{| align="center" border="1" cellpadding="2" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | {| align="center" border="1" cellpadding="2" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 19. Simple Qualifiers of Propositions (Version 2)}\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| − | | align="right" | <math>u:</math><br><math>v:</math> | + | | align="right" | <math>u:\!</math><br><math>v:\!</math> |
| 1100<br>1010 | | 1100<br>1010 | ||
| <math>f\!</math> | | <math>f\!</math> | ||
| − | | <math>(\ell_{11})</math><br><math>\text{No } u </math><br><math>\text{is } v </math> | + | | <math>(\ell_{11})\!</math><br><math>\text{No } u \!</math><br><math>\text{is } v \!</math> |
| − | | <math>(\ell_{10})</math><br><math>\text{No } u </math><br><math>\text{is }(v)</math> | + | | <math>(\ell_{10})\!</math><br><math>\text{No } u \!</math><br><math>\text{is }(v)\!</math> |
| − | | <math>(\ell_{01})</math><br><math>\text{No }(u)</math><br><math>\text{is } v </math> | + | | <math>(\ell_{01})\!</math><br><math>\text{No }(u)\!</math><br><math>\text{is } v \!</math> |
| − | | <math>(\ell_{00})</math><br><math>\text{No }(u)</math><br><math>\text{is }(v)</math> | + | | <math>(\ell_{00})\!</math><br><math>\text{No }(u)\!</math><br><math>\text{is }(v)\!</math> |
| − | | <math> \ell_{00} </math><br><math>\text{Some }(u)</math><br><math>\text{is }(v)</math> | + | | <math> \ell_{00} \!</math><br><math>\text{Some }(u)\!</math><br><math>\text{is }(v)\!</math> |
| − | | <math> \ell_{01} </math><br><math>\text{Some }(u)</math><br><math>\text{is } v </math> | + | | <math> \ell_{01} \!</math><br><math>\text{Some }(u)\!</math><br><math>\text{is } v \!</math> |
| − | | <math> \ell_{10} </math><br><math>\text{Some } u </math><br><math>\text{is }(v)</math> | + | | <math> \ell_{10}~\!</math><br><math>\text{Some } u \!</math><br><math>\text{is }(v)\!</math> |
| − | | <math> \ell_{11} </math><br><math>\text{Some } u </math><br><math>\text{is } v </math> | + | | <math> \ell_{11} \!</math><br><math>\text{Some } u \!</math><br><math>\text{is } v \!</math> |
|- | |- | ||
| − | | <math>f_0</math> | + | | <math>f_0\!</math> |
| 0000 | | 0000 | ||
| − | | <math>(~)</math> | + | | <math>(~)\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 2,029: | Line 2,090: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_1</math> | + | | <math>f_1\!</math> |
| 0001 | | 0001 | ||
| <math>(u)(v)\!</math> | | <math>(u)(v)\!</math> | ||
| Line 2,041: | Line 2,102: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_2</math> | + | | <math>f_2\!</math> |
| 0010 | | 0010 | ||
| <math>(u) v\!</math> | | <math>(u) v\!</math> | ||
| Line 2,053: | Line 2,114: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_4</math> | + | | <math>f_4\!</math> |
| 0100 | | 0100 | ||
| <math>u (v)\!</math> | | <math>u (v)\!</math> | ||
| Line 2,065: | Line 2,126: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_8</math> | + | | <math>f_8\!</math> |
| 1000 | | 1000 | ||
| <math>u v\!</math> | | <math>u v\!</math> | ||
| Line 2,077: | Line 2,138: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_3</math> | + | | <math>f_3\!</math> |
| 0011 | | 0011 | ||
| − | | <math>(u)\!</math> | + | | <math>(u)~\!</math> |
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| Line 2,089: | Line 2,150: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{12}</math> | + | | <math>f_{12}\!</math> |
| 1100 | | 1100 | ||
| <math>u\!</math> | | <math>u\!</math> | ||
| Line 2,101: | Line 2,162: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_6</math> | + | | <math>f_6\!</math> |
| 0110 | | 0110 | ||
| <math>(u, v)\!</math> | | <math>(u, v)\!</math> | ||
| Line 2,113: | Line 2,174: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_9</math> | + | | <math>f_9\!</math> |
| 1001 | | 1001 | ||
| <math>((u, v))\!</math> | | <math>((u, v))\!</math> | ||
| Line 2,125: | Line 2,186: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_5</math> | + | | <math>f_5\!</math> |
| 0101 | | 0101 | ||
| <math>(v)\!</math> | | <math>(v)\!</math> | ||
| Line 2,137: | Line 2,198: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{10}</math> | + | | <math>f_{10}\!</math> |
| 1010 | | 1010 | ||
| <math>v\!</math> | | <math>v\!</math> | ||
| Line 2,149: | Line 2,210: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_7</math> | + | | <math>f_7\!</math> |
| 0111 | | 0111 | ||
| <math>(u v)\!</math> | | <math>(u v)\!</math> | ||
| Line 2,161: | Line 2,222: | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
|- | |- | ||
| − | | <math>f_{11}</math> | + | | <math>f_{11}\!</math> |
| 1011 | | 1011 | ||
| <math>(u (v))\!</math> | | <math>(u (v))\!</math> | ||
| Line 2,173: | Line 2,234: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{13}</math> | + | | <math>f_{13}\!</math> |
| 1101 | | 1101 | ||
| <math>((u) v)\!</math> | | <math>((u) v)\!</math> | ||
| Line 2,185: | Line 2,246: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{14}</math> | + | | <math>f_{14}\!</math> |
| 1110 | | 1110 | ||
| − | | <math>((u)(v))\!</math> | + | | <math>((u)(v))~\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 2,197: | Line 2,258: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
|- | |- | ||
| − | | <math>f_{15}</math> | + | | <math>f_{15}\!</math> |
| 1111 | | 1111 | ||
| − | | <math>((~))</math> | + | | <math>((~))\!</math> |
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| style="background:white; color:black" | 0 | | style="background:white; color:black" | 0 | ||
| Line 2,208: | Line 2,269: | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| style="background:black; color:white" | 1 | | style="background:black; color:white" | 1 | ||
| − | |}<br> | + | |} |
| + | |||
| + | <br> | ||
{| align="center" border="1" cellpadding="2" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | {| align="center" border="1" cellpadding="2" cellspacing="0" style="font-weight:bold; text-align:center; width:96%" | ||
| − | |+ | + | |+ style="height:25px" | |
| + | <math>\text{Table 20. Relation of Quantifiers to Higher Order Propositions}\!</math> | ||
|- style="background:ghostwhite" | |- style="background:ghostwhite" | ||
| − | | <math>\text{Mnemonic}</math> | + | | <math>\text{Mnemonic}\!</math> |
| − | | <math>\text{Category}</math> | + | | <math>\text{Category}\!</math> |
| − | | <math>\text{Classical Form}</math> | + | | <math>\text{Classical Form}\!</math> |
| − | | <math>\text{Alternate Form}</math> | + | | <math>\text{Alternate Form}\!</math> |
| − | | <math>\text{Symmetric Form}</math> | + | | <math>\text{Symmetric Form}\!</math> |
| − | | <math>\text{Operator}</math> | + | | <math>\text{Operator}\!</math> |
|- | |- | ||
| − | | <math>\text{E}\!</math><br><math>\text{Exclusive}</math> | + | | <math>\text{E}\!</math><br><math>\text{Exclusive}\!</math> |
| − | | <math>\text{Universal}</math><br><math>\text{Negative}</math> | + | | <math>\text{Universal}\!</math><br><math>\text{Negative}\!</math> |
| − | | <math>\text{All} | + | | <math>\text{All}~ u ~\text{is}~ (v)\!</math> |
| | | | ||
| − | | <math>\text{No} | + | | <math>\text{No}~ u ~\text{is}~ v \!</math> |
| − | | <math>(\ell_{11})</math> | + | | <math>{(\ell_{11})}\!</math> |
|- | |- | ||
| − | | <math>\text{A}\!</math><br><math>\text{Absolute}</math> | + | | <math>\text{A}\!</math><br><math>\text{Absolute}~\!</math> |
| − | | <math>\text{Universal}</math><br><math>\text{Affirmative}</math> | + | | <math>\text{Universal}\!</math><br><math>\text{Affirmative}\!</math> |
| − | | <math>\text{All} | + | | <math>\text{All}~ u ~\text{is}~ v \!</math> |
| | | | ||
| − | | <math>\text{No} | + | | <math>\text{No}~ u ~\text{is}~ (v)\!</math> |
| − | | <math>(\ell_{10})</math> | + | | <math>{(\ell_{10})}\!</math> |
|- | |- | ||
| | | | ||
| | | | ||
| − | | <math>\text{All} | + | | <math>\text{All}~ v ~\text{is}~ u \!</math> |
| − | | <math>\text{No} | + | | <math>\text{No}~ v ~\text{is}~ (u)\!</math> |
| − | | <math>\text{No} | + | | <math>\text{No}~ (u) ~\text{is}~ v \!</math> |
| − | | <math>(\ell_{01})</math> | + | | <math>{(\ell_{01})}\!</math> |
|- | |- | ||
| | | | ||
| | | | ||
| − | | <math>\text{All} | + | | <math>\text{All}~ (v) ~\text{is}~ u \!</math> |
| − | | <math>\text{No} | + | | <math>\text{No}~ (v) ~\text{is}~ (u)\!</math> |
| − | | <math>\text{No} | + | | <math>\text{No}~ (u) ~\text{is}~ (v)\!</math> |
| − | | <math>(\ell_{00})</math> | + | | <math>{(\ell_{00})}\!</math> |
|- | |- | ||
| | | | ||
| | | | ||
| − | | <math>\text{Some} | + | | <math>\text{Some}~ (u) ~\text{is}~ (v)\!</math> |
| | | | ||
| − | | <math>\text{Some} | + | | <math>\text{Some}~ (u) ~\text{is}~ (v)\!</math> |
| − | | <math>\ell_{00}\!</math> | + | | <math>{\ell_{00}}\!</math> |
|- | |- | ||
| | | | ||
| | | | ||
| − | | <math>\text{Some} | + | | <math>\text{Some}~ (u) ~\text{is}~ v\!</math> |
| | | | ||
| − | | <math>\text{Some} | + | | <math>\text{Some}~ (u) ~\text{is}~ v\!</math> |
| − | | <math>\ell_{01}\!</math> | + | | <math>{\ell_{01}}\!</math> |
|- | |- | ||
| − | | <math>\text{O}\!</math><br><math>\text{Obtrusive}</math> | + | | <math>\text{O}\!</math><br><math>\text{Obtrusive}\!</math> |
| − | | <math>\text{Particular}</math><br><math>\text{Negative}</math> | + | | <math>\text{Particular}\!</math><br><math>\text{Negative}\!</math> |
| − | | <math>\text{Some} | + | | <math>\text{Some}~ u ~\text{is}~ (v)\!</math> |
| | | | ||
| − | | <math>\text{Some} | + | | <math>\text{Some}~ u ~\text{is}~ (v)\!</math> |
| − | | <math>\ell_{10}\!</math> | + | | <math>{\ell_{10}}\!</math> |
|- | |- | ||
| − | | <math>\text{I}\!</math><br><math>\text{Indefinite}</math> | + | | <math>\text{I}\!</math><br><math>\text{Indefinite}\!</math> |
| − | | <math>\text{Particular}</math><br><math>\text{Affirmative}</math> | + | | <math>\text{Particular}\!</math><br><math>\text{Affirmative}\!</math> |
| − | | <math>\text{Some} | + | | <math>\text{Some}~ u ~\text{is}~ v\!</math> |
| | | | ||
| − | | <math>\text{Some} | + | | <math>\text{Some}~ u ~\text{is}~ v\!</math> |
| − | | <math>\ell_{11}\!</math> | + | | <math>{\ell_{11}}\!</math> |
| − | |}<br> | + | |} |
| + | |||
| + | <br> | ||
==Appendix : Generalized Umpire Operators== | ==Appendix : Generalized Umpire Operators== | ||
| Line 2,282: | Line 2,348: | ||
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| − | | <math>\Upsilon : \bigcup_{\ell = 1, 2, 3} ((\mathbb{B}^k \to \mathbb{B})^\ell \to \mathbb{B}).</math> | + | | <math>\Upsilon : \bigcup_{\ell = 1, 2, 3} ((\mathbb{B}^k \to \mathbb{B})^\ell \to \mathbb{B}).\!</math> |
|} | |} | ||
| Line 2,290: | Line 2,356: | ||
| <math>\Upsilon_p^r q = \Upsilon (p, q, r)\!</math> | | <math>\Upsilon_p^r q = \Upsilon (p, q, r)\!</math> | ||
|- | |- | ||
| − | | <math>\Upsilon_p^r : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}</math> | + | | <math>\Upsilon_p^r : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}\!</math> |
|} | |} | ||
| − | The intention of this operator is that we evaluate the proposition <math>q\!</math> on each model of the proposition <math>p\!</math> and combine the results according to the method indicated by the connective parameter <math>r.\!</math> In principle, the index <math>r\!</math> might specify any connective on as many as <math>2^k\!</math> arguments, but usually we have in mind a much simpler form of combination, most often either collective products or collective sums. By convention, each of the accessory indices <math>p, r\!</math> is assigned a default value that is understood to be in force when the corresponding argument place is left blank, specifically, the constant proposition <math>1 : \mathbb{B}^k \to \mathbb{B}</math> for the lower index <math>p,\!</math> and the continued conjunction or continued product operation <math>\textstyle\prod</math> for the upper index <math>r.\!</math> Taking the upper default value gives license to the following readings: | + | The intention of this operator is that we evaluate the proposition <math>q\!</math> on each model of the proposition <math>p\!</math> and combine the results according to the method indicated by the connective parameter <math>r.\!</math> In principle, the index <math>r\!</math> might specify any connective on as many as <math>2^k\!</math> arguments, but usually we have in mind a much simpler form of combination, most often either collective products or collective sums. By convention, each of the accessory indices <math>p, r\!</math> is assigned a default value that is understood to be in force when the corresponding argument place is left blank, specifically, the constant proposition <math>1 : \mathbb{B}^k \to \mathbb{B}\!</math> for the lower index <math>p,\!</math> and the continued conjunction or continued product operation <math>\textstyle\prod\!</math> for the upper index <math>r.\!</math> Taking the upper default value gives license to the following readings: |
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| − | | <math>\Upsilon_p (q) = \Upsilon (p, q) = \Upsilon (p, q, \textstyle\prod).</math> | + | | <math>\Upsilon_p (q) = \Upsilon (p, q) = \Upsilon (p, q, \textstyle\prod).\!</math> |
|- | |- | ||
| − | | <math>\Upsilon_p = \Upsilon (p, \underline{~~}, \textstyle\prod) : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}.</math> | + | | <math>\Upsilon_p = \Upsilon (p, \underline{~~}, \textstyle\prod) : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}.\!</math> |
|} | |} | ||
| − | This means that <math>\Upsilon_p (q) = 1\!</math> if and only if <math>q\!</math> holds for all models of <math>p.\!</math> In propositional terms, this is tantamount to the assertion that <math>p \Rightarrow q,</math> or that <math>\underline{(p (q))} = \underline{1}.</math> | + | This means that <math>\Upsilon_p (q) = 1\!</math> if and only if <math>q\!</math> holds for all models of <math>p.\!</math> In propositional terms, this is tantamount to the assertion that <math>p \Rightarrow q,\!</math> or that <math>\underline{(p (q))} = \underline{1}.\!</math> |
Throwing in the lower default value permits the following abbreviations: | Throwing in the lower default value permits the following abbreviations: | ||
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| − | | <math>\Upsilon q = \Upsilon (q) = \Upsilon_1 (q) = \Upsilon (1, q, \textstyle\prod).</math> | + | | <math>\Upsilon q = \Upsilon (q) = \Upsilon_1 (q) = \Upsilon (1, q, \textstyle\prod).\!</math> |
|- | |- | ||
| − | | <math>\Upsilon = \Upsilon (1, \underline{~~}, \textstyle\prod)) : (\mathbb{B}^k\ \to \mathbb{B}) \to \mathbb{B}.</math> | + | | <math>\Upsilon = \Upsilon (1, \underline{~~}, \textstyle\prod)) : (\mathbb{B}^k\ \to \mathbb{B}) \to \mathbb{B}.\!</math> |
|} | |} | ||
| − | This means that <math>\Upsilon q = 1\!</math> if and only if <math>q\!</math> holds for the whole universe of discourse in question, that is, if and only <math>q\!</math> is the constantly true proposition <math>1 : \mathbb{B}^k \to \mathbb{B}.</math> The ambiguities of this usage are not a problem so long as we distinguish the context of definition from the context of application and restrict all shorthand notations to the latter. | + | This means that <math>\Upsilon q = 1\!</math> if and only if <math>q\!</math> holds for the whole universe of discourse in question, that is, if and only <math>q\!</math> is the constantly true proposition <math>1 : \mathbb{B}^k \to \mathbb{B}.\!</math> The ambiguities of this usage are not a problem so long as we distinguish the context of definition from the context of application and restrict all shorthand notations to the latter. |
==References== | ==References== | ||
| Line 2,328: | Line 2,394: | ||
| align="left" | Course: | | align="left" | Course: | ||
| align="center" | Engineering 690, Graduate Project | | align="center" | Engineering 690, Graduate Project | ||
| − | | align="right" | | + | | align="right" | Winter Term, January 1995 |
|- | |- | ||
| align="left" | Supervisors: | | align="left" | Supervisors: | ||
| − | | align="center" | | + | | align="center" | M.A. Zohdy and F. Mili |
| align="right" | Oakland University | | align="right" | Oakland University | ||
|} | |} | ||
| Line 2,344: | Line 2,410: | ||
===Functional Logic=== | ===Functional Logic=== | ||
| + | |||
| + | ====Inquiry List==== | ||
| + | |||
| + | * http://web.archive.org/web/20140821214025/http://stderr.org/pipermail/inquiry/2004-March/thread.html#1256 | ||
| + | # http://web.archive.org/web/20090303000827/http://stderr.org/pipermail/inquiry/2004-March/001256.html | ||
| + | # http://web.archive.org/web/20090303001935/http://stderr.org/pipermail/inquiry/2004-March/001257.html | ||
| + | # http://web.archive.org/web/20090303002148/http://stderr.org/pipermail/inquiry/2004-March/001258.html | ||
| + | # http://web.archive.org/web/20090303001240/http://stderr.org/pipermail/inquiry/2004-March/001259.html | ||
| + | # http://web.archive.org/web/20090303001940/http://stderr.org/pipermail/inquiry/2004-March/001260.html | ||
| + | # http://web.archive.org/web/20090303002026/http://stderr.org/pipermail/inquiry/2004-March/001261.html | ||
====Ontology List==== | ====Ontology List==== | ||
| − | * http://suo.ieee.org/ontology/thrd2.html#05480 | + | * http://web.archive.org/web/20090302185041/http://suo.ieee.org/ontology/thrd2.html#05480 |
| − | # http://suo.ieee.org/ontology/msg05480.html | + | # http://web.archive.org/web/20090303202815/http://suo.ieee.org/ontology/msg05480.html |
| − | # http://suo.ieee.org/ontology/msg05481.html | + | # http://web.archive.org/web/20090302145522/http://suo.ieee.org/ontology/msg05481.html |
| − | # http://suo.ieee.org/ontology/msg05482.html | + | # http://web.archive.org/web/20090302145531/http://suo.ieee.org/ontology/msg05482.html |
| − | # http://suo.ieee.org/ontology/msg05483.html | + | # http://web.archive.org/web/20090303203051/http://suo.ieee.org/ontology/msg05483.html |
| − | # http://suo.ieee.org/ontology/msg05484.html | + | # http://web.archive.org/web/20090303203442/http://suo.ieee.org/ontology/msg05484.html |
| − | # http://suo.ieee.org/ontology/msg05485.html | + | # http://web.archive.org/web/20090302145538/http://suo.ieee.org/ontology/msg05485.html |
| + | |||
| + | ====NKS Forum==== | ||
| − | = | + | * http://web.archive.org/web/20131120210604/http://forum.wolframscience.com/archive/topic/254.html |
| + | * http://web.archive.org/web/20090302144746/http://forum.wolframscience.com/showthread.php?threadid=254 | ||
| − | + | ===Inquiry Driven Systems=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====NKS Forum==== | ====NKS Forum==== | ||
| − | * http:// | + | * http://web.archive.org/web/20131104033846/http://forum.wolframscience.com/archive/topic/598.html |
| − | + | * http://web.archive.org/web/20160406171418/http://forum.wolframscience.com/showthread.php?threadid=598 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # http://web.archive.org/web/20090302150057/http://forum.wolframscience.com/showthread.php?postid=1957#post1957 | |
| + | # http://web.archive.org/web/20090302145607/http://forum.wolframscience.com/showthread.php?postid=1960#post1960 | ||
| + | # http://web.archive.org/web/20090302150102/http://forum.wolframscience.com/showthread.php?postid=1961#post1961 | ||
| + | # http://web.archive.org/web/20090302150134/http://forum.wolframscience.com/showthread.php?postid=1962#post1962 | ||
| + | # http://web.archive.org/web/20090302145918/http://forum.wolframscience.com/showthread.php?postid=1964#post1964 | ||
| + | # http://web.archive.org/web/20090302145303/http://forum.wolframscience.com/showthread.php?postid=1966#post1966 | ||
| + | # http://web.archive.org/web/20090302150013/http://forum.wolframscience.com/showthread.php?postid=1968#post1968 | ||
[[Category:Adaptive Systems]] | [[Category:Adaptive Systems]] | ||
[[Category:Artificial Intelligence]] | [[Category:Artificial Intelligence]] | ||
| + | [[Category:Charles Sanders Peirce]] | ||
[[Category:Combinatorics]] | [[Category:Combinatorics]] | ||
[[Category:Computer Science]] | [[Category:Computer Science]] | ||
Latest revision as of 18:45, 18 March 2020
Author: Jon Awbrey
Abstract
This report discusses C.S. Peirce's treatment of analogy, placing it in relation to his overall theory of inquiry. The first order of business is to introduce the three fundamental types of reasoning that Peirce adopted from classical logic. In Peirce's analysis both inquiry and analogy are complex programs of reasoning that develop through stages of these three types, although normally in different orders.
Note on notation. The discussion that follows uses minimal negations, expressed as bracketed tuples of the form \(\texttt{(} e_1 \texttt{,} \ldots \texttt{,} e_k \texttt{)},\!\) and logical conjunctions, expressed as concatenated tuples of the form \(e_1 ~\ldots~ e_k,\!\) as the sole expression-forming operations of a calculus for boolean-valued functions or propositions. The expressions of this calculus parse into data structures whose underlying graphs are called cacti by graph theorists. Hence the name cactus language for this dialect of propositional calculus.
1. Three Types of Reasoning
1.1. Types of Reasoning in Aristotle
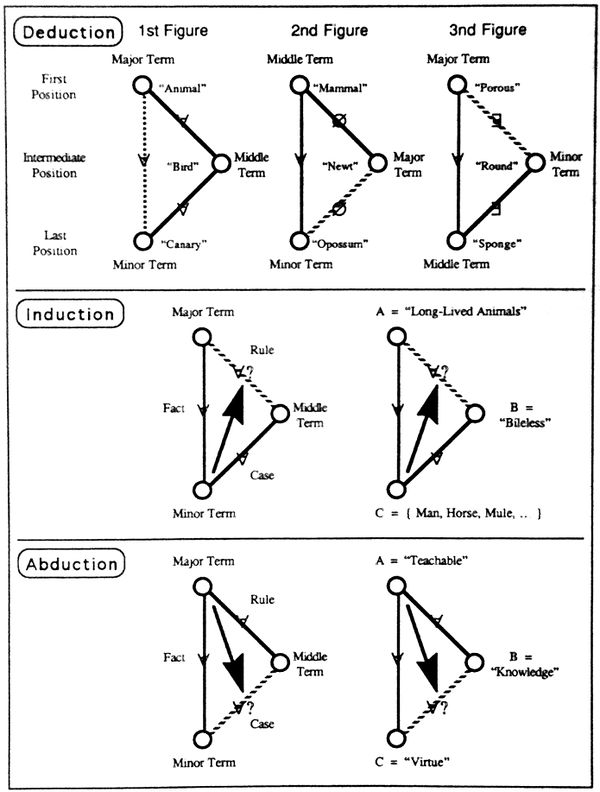
|
| \(\text{Figure 1. Types of Reasoning in Aristotle}\!\) |
1.2. Types of Reasoning in C.S. Peirce
Here we present one of Peirce's earliest treatments of the three types of reasoning, from his Harvard Lectures of 1865 “On the Logic of Science”. It illustrates how one and the same proposition might be reached from three different directions, as the end result of an inference in each of the three modes.
| We have then three different kinds of inference: |
| Deduction or inference à priori, |
| Induction or inference à particularis, |
| Hypothesis or inference à posteriori. |
| (Peirce, CE 1, p. 267). |
| If I reason that certain conduct is wise because it has a character which belongs only to wise things, I reason à priori. |
| If I think it is wise because it once turned out to be wise, that is, if I infer that it is wise on this occasion because it was wise on that occasion, I reason inductively [à particularis]. |
| But if I think it is wise because a wise man does it, I then make the pure hypothesis that he does it because he is wise, and I reason à posteriori. |
| (Peirce, CE 1, p. 180). |
Suppose we make the following assignments:
| A | = | “Wisdom”, | |
| B | = | “a certain character”, | |
| C | = | “a certain conduct”, | |
| D | = | “done by a wise man”, | |
| E | = | “a certain occasion”. |
Recognizing that a little more concreteness will aid the understanding, let us make the following substitutions in Peirce's example:
| B | = | “Benevolence”, | a certain character, |
| C | = | “Contributes to Charity”, | a certain conduct, |
| E | = | “Earlier today”, | a certain occasion. |
The converging operation of all three reasonings is shown in Figure 2.
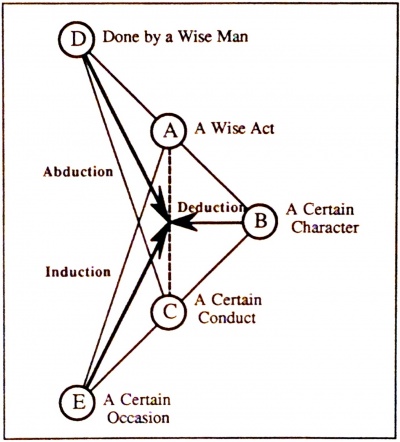
|
| \(\text{Figure 2. A Triply Wise Act}\!\) |
The common proposition that concludes each argument is AC, to wit, “contributing to charity is wise”.
Deduction could have obtained the Fact AC from the Rule AB, “benevolence is wisdom”, along with the Case BC, “contributing to charity is benevolent”.
Induction could have gathered the Rule AC, after a manner of saying that “contributing to charity is exemplary of wisdom”, from the Fact AE, “the act of earlier today is wise”, along with the Case CE, “the act of earlier today was an instance of contributing to charity”.
Abduction could have guessed the Case AC, in a style of expression stating that “contributing to charity is explained by wisdom”, from the Fact DC, “contributing to charity is done by this wise man”, and the Rule DA, “everything that is wise is done by this wise man”. Thus, a wise man, who happens to do all of the wise things that there are to do, may nevertheless contribute to charity for no good reason, and even be known to be charitable to a fault. But all of this notwithstanding, on seeing the wise man contribute to charity we may find it natural to conjecture, in effect, to consider it as a possibility worth examining further, that charity is indeed a mark of his wisdom, and not just the accidental trait or the immaterial peculiarity of his character — in essence, that wisdom is the reason he contributes to charity.
1.3. Comparison of the Analyses
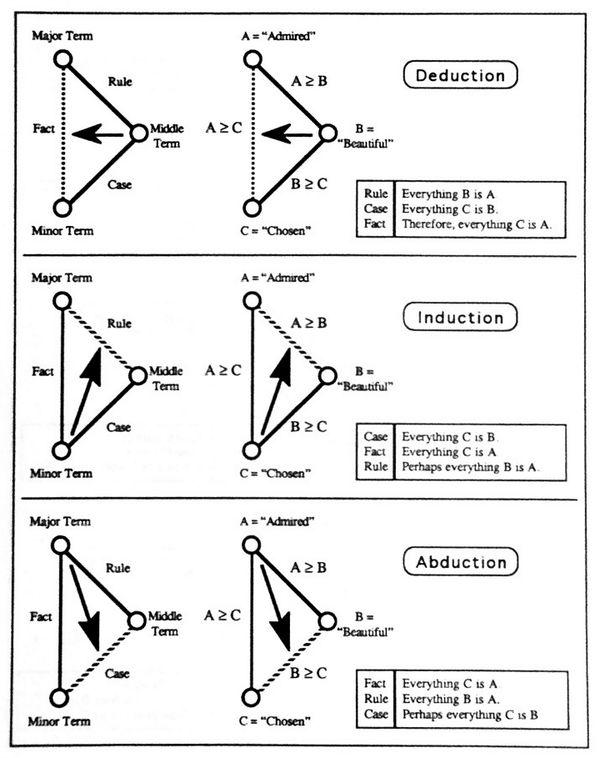
|
| \(\text{Figure 3. Types of Reasoning in Transition}\!\) |
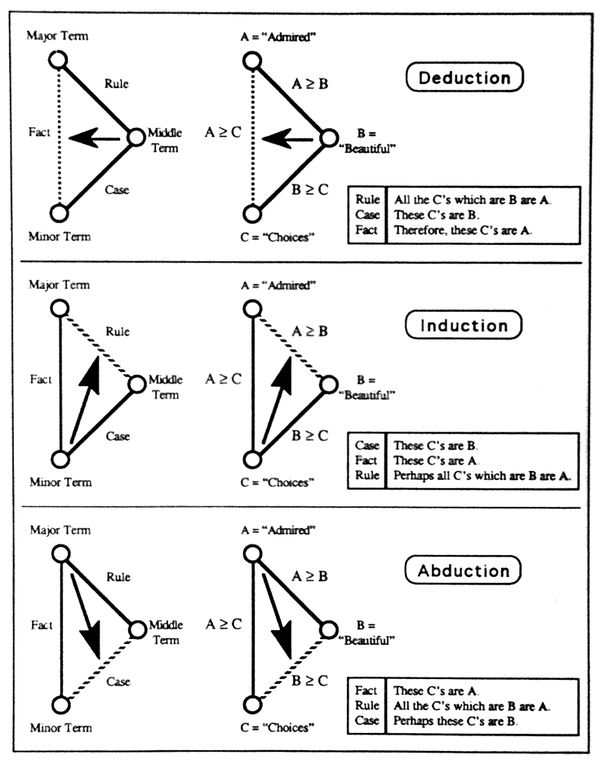
|
| \(\text{Figure 4. Types of Reasoning in Peirce}\!\) |
1.4. Aristotle's “Apagogy” : Abductive Reasoning as Problem Reduction
Peirce's notion of abductive reasoning was derived from Aristotle's treatment of it in the Prior Analytics. Aristotle's discussion begins with an example that may appear incidental, but the question and its analysis are echoes of an important investigation that was pursued in one of Plato's Dialogues, the Meno. This inquiry is concerned with the possibility of knowledge and the relationship between knowledge and virtue, or between their objects, the true and the good. It is not just because it forms a recurring question in philosophy, but because it preserves a certain correspondence between its form and its content, that we shall find this example increasingly relevant to our study.
A couple of notes on the reading may be helpful. The Greek text seems to imply a geometric diagram, in which directed line segments AB, BC, AC are used to indicate logical relations between pairs of the terms in A, B, C. We have two options for reading these line labels, either as implications or as subsumptions, as in the following two paradigms for interpretation.
| Read as Implications: | ||
| AB | = | A ⇐ B, |
| BC | = | B ⇐ C, |
| AC | = | A ⇐ C. |
| Read as Subsumptions: | ||
| AB | = | A subsumes B, |
| BC | = | B subsumes C, |
| AC | = | A subsumes C. |
Here, “X subsumes Y” means that “X applies to all Y”, or that “X is predicated of all Y”. When there is no danger of confusion we may write this as “X ≥ Y”.
|
We have Reduction (απαγωγη, abduction): (1) when it is obvious that the first term applies to the middle, but that the middle applies to the last term is not obvious, yet nevertheless is more probable or not less probable than the conclusion; or (2) if there are not many intermediate terms between the last and the middle; for in all such cases the effect is to bring us nearer to knowledge. (1) E.g., let A stand for “that which can be taught”, B for “knowledge”, and C for “morality”. Then that knowledge can be taught is evident; but whether virtue is knowledge is not clear. Then if BC is not less probable or is more probable than AC, we have reduction; for we are nearer to knowledge for having introduced an additional term, whereas before we had no knowledge that AC is true. (2) Or again we have reduction if there are not many intermediate terms between B and C; for in this case too we are brought nearer to knowledge. E.g., suppose that D is “to square”, E “rectilinear figure”, and F “circle”. Assuming that between E and F there is only one intermediate term — that the circle becomes equal to a rectilinear figure by means of lunules — we should approximate to knowledge. |
| (Aristotle, “Prior Analytics” 2.25) |
The method of abductive reasoning bears a close relation to the sense of reduction in which we speak of one question reducing to another. The question being asked is “Can virtue be taught?” The type of answer which develops is the following.
If virtue is a form of understanding, and if we are willing to grant that understanding can be taught, then virtue can be taught. In this way of approaching the problem, by detour and indirection, the form of abductive reasoning is used to shift the attack from the original question, whether virtue can be taught, to the hopefully easier question, whether virtue is a form of understanding.
The logical structure of the process of hypothesis formation in the first example follows the pattern of “abduction to a case”, whose abstract form is diagrammed and schematized in Figure 5.
o-------------------------------------------------o | | | T = Teachable | | o | | ^^ | | | \ | | | \ | | | \ | | | \ | | | \ R U L E | | | \ | | | \ | | F | \ | | | \ | | A | \ | | | o U = Understanding | | C | ^ | | | / | | T | / | | | / | | | / | | | / C A S E | | | / | | | / | | | / | | | / | | |/ | | o | | V = Virtue | | | | T = Teachable (didacton) | | U = Understanding (epistemé) | | V = Virtue (areté) | | | | T is the Major term | | U is the Middle term | | V is the Minor term | | | | TV = "T of V" = Fact in Question | | TU = "T of U" = Rule in Evidence | | UV = "U of V" = Case in Question | | | | Schema for Abduction to a Case: | | | | Fact: V => T? | | Rule: U => T. | | ---------------- | | Case: V => U? | o-------------------------------------------------o Figure 5. Teachability, Understanding, Virtue |
1.5. Aristotle's “Paradigm” : Reasoning by Analogy or Example
Here we present Aristotle's treatment of analogical inference or “reasoning by example”. The Greek word for this is παραδειγμα, from which we derive the English word “paradigm”, and it suggests a kind of “side-show”, or a parallel comparison of cases.
|
We have an Example (παραδειγμα, or analogy) when the major extreme is shown to be applicable to the middle term by means of a term similar to the third. It must be known both that the middle applies to the third term and that the first applies to the term similar to the third. E.g., let A be “bad”, B “to make war on neighbors”, C “Athens against Thebes”, and D “Thebes against Phocis”. Then if we require to prove that war against Thebes is bad, we must be satisfied that war against neighbors is bad. Evidence of this can be drawn from similar examples, e.g., that war by Thebes against Phocis is bad. Then since war against neighbors is bad, and war against Thebes is against neighbors, it is evident that war against Thebes is bad. |
| (Aristotle, “Prior Analytics” 2.24) |
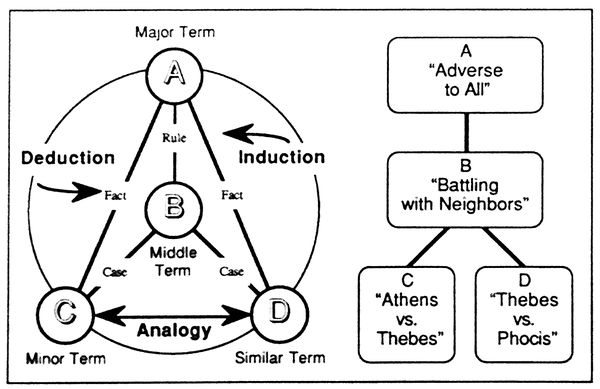
|
| \(\operatorname{Figure~6.~Aristotle's} ~ {}^{\backprime\backprime}\text{Paradigm}{}^{\prime\prime}\!\) |
1.6. Peirce's Formulation of Analogy
Note. A few changes in Peirce's notation have been made to facilitate comparison between the two versions.
Version 1. “On the Natural Classification of Arguments” (1867)
|
The formula of analogy is as follows: \(S^{\prime}, S^{\prime\prime}, ~\operatorname{and}~ S^{\prime\prime\prime}\!\) are taken at random from such a class that their characters at random are such as \({P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}}.\!\) |
|
\(\begin{matrix} T ~\operatorname{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\operatorname{are}~ Q; \\[4pt] \therefore T ~\operatorname{is}~ Q. \end{matrix}\) |
Such an argument is double. It combines the two following: |
|
\(\begin{matrix} 1. \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\operatorname{are~taken~as~being}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\operatorname{are}~ Q; \\[4pt] \therefore ~(\operatorname{By~induction})~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime} ~\operatorname{is}~ Q, \\[4pt] T ~\operatorname{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}; \\[4pt] \therefore ~(\operatorname{Deductively})~ T ~\operatorname{is}~ Q. \end{matrix}\) |
|
\(\begin{matrix} 2. \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\operatorname{are,~for~instance,}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, \\[4pt] T ~\operatorname{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}; \\[4pt] \therefore ~(\operatorname{By~hypothesis})~ T ~\operatorname{has~the~common~characters~of}~ S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\operatorname{are}~ Q; \\[4pt] \therefore ~(\operatorname{Deductively})~ T ~\operatorname{is}~ Q. \end{matrix}\) |
Owing to its double character, analogy is very strong with only a moderate number of instances. |
| (Peirce, CP 2.513; CE 2, 46–47) |
The form of this analysis is illustrated in Figure 7.
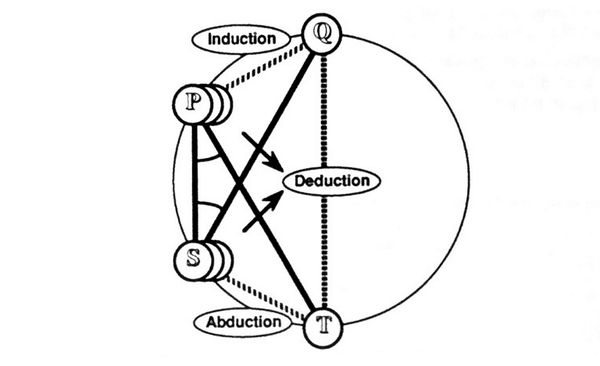
|
| \(\operatorname{Figure~7.~Peirce's~Formulation~of~Analogy~(Version~1)}\!\) |
Version 2. “A Theory of Probable Inference” (1883)
|
The formula of the analogical inference presents, therefore, three premisses, thus: \(S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime},\!\) are a random sample of some undefined class, \(X,\!\) of whose characters \(P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime},\!\) are samples, |
|
\(\begin{matrix} T ~\text{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}; \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, ~\text{are}~ Q\operatorname{'s}; \\[4pt] \text{Hence,}~ T ~\text{is a}~ Q. \end{matrix}\) |
|
We have evidently here an induction and an hypothesis followed by a deduction; thus: |
|
\(\begin{array}{l|l} \text{Every}~ X ~\text{is, for example,}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, ~\text{etc.}, & S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, ~\text{etc., are samples of the}~ X\operatorname{'s}, \\[4pt] T ~\text{is found to be}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, ~\text{etc.}; & S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, ~\text{etc., are found to be}~ Q\operatorname{'s}; \\[4pt] \text{Hence, hypothetically,}~ T ~\text{is an}~ X. & \text{Hence, inductively, every}~ X ~\text{is a}~ Q. \end{array}\) |
|
\(\text{Hence, deductively,}~ T ~\text{is a}~ Q.\!\) |
| (Peirce, CP 2.733) |
The form of this analysis is illustrated in Figure 8.
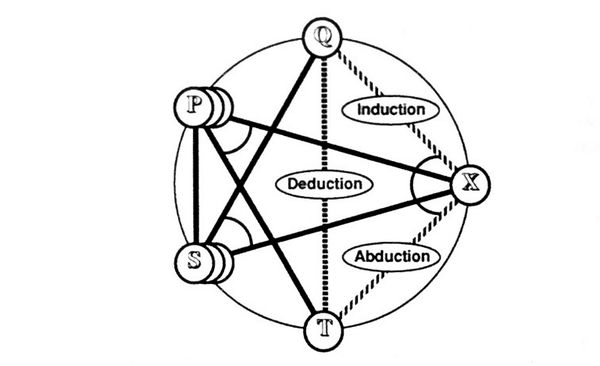
|
| \(\operatorname{Figure~8.~Peirce's~Formulation~of~Analogy~(Version~2)}\!\) |
1.7. Dewey's “Sign of Rain” : An Example of Inquiry
To illustrate the place of the sign relation in inquiry we begin with Dewey's elegant and simple example of reflective thinking in everyday life.
|
A man is walking on a warm day. The sky was clear the last time he observed it; but presently he notes, while occupied primarily with other things, that the air is cooler. It occurs to him that it is probably going to rain; looking up, he sees a dark cloud between him and the sun, and he then quickens his steps. What, if anything, in such a situation can be called thought? Neither the act of walking nor the noting of the cold is a thought. Walking is one direction of activity; looking and noting are other modes of activity. The likelihood that it will rain is, however, something suggested. The pedestrian feels the cold; he thinks of clouds and a coming shower. |
| (Dewey 1991, 6–7) |
In this narrative we can identify the characters of the sign relation as follows: coolness is a Sign of the Object rain, and the Interpretant is the thought of the rain's likelihood. In his 1910 description of reflective thinking Dewey distinguishes two phases, “a state of perplexity, hesitation, doubt” and “an act of search or investigation” (Dewey 1991, 9), comprehensive stages which are further refined in his later model of inquiry. In this example, reflection is the act of the interpreter which establishes a fund of connections between the sensory shock of coolness and the objective danger of rain, by way of his impression that rain is likely. But reflection is more than irresponsible speculation. In reflection the interpreter acts to charge or defuse the thought of rain (the probability of rain in thought) by seeking other signs which this thought implies and evaluating the thought according to the results of this search.
Figure 9 illustrates Dewey's “Sign of Rain” example, tracing the structure and function of the sign relation as it informs the activity of inquiry, including both the movements of surprise explanation and intentional action. The dyadic faces of the sign relation are labeled with just a few of the loosest terms that apply, indicating the “significance” of signs for eventual occurrences and the “correspondence&rdqu; of ideas with external orientations. Nothing essential is meant by these dyadic role distinctions, since it is only in special or degenerate cases that their shadowy projections can maintain enough information to determine the original sign relation.
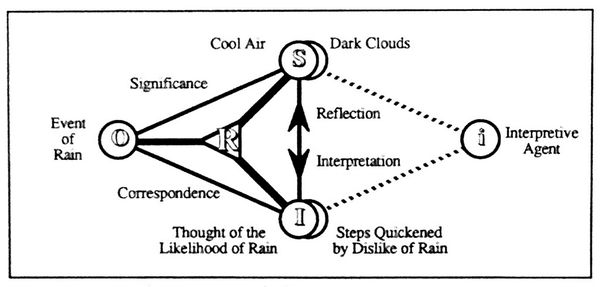
|
| \(\operatorname{Figure~9.~Dewey's} ~ {}^{\backprime\backprime}\text{Sign of Rain}{}^{\prime\prime} ~ \text{Example}\!\) |
If we follow this example far enough to consider the import of thought for action, we realize that the subsequent conduct of the interpreter, progressing up through the natural conclusion of the episode — the quickening steps, seeking shelter in time to escape the rain — all of these acts form a series of further interpretants, contingent on the active causes of the individual, for the originally recognized signs of rain and for the first impressions of the actual case. Just as critical reflection develops the associated and alternative signs which gather about an idea, pragmatic interpretation explores the consequential and contrasting actions which give effective and testable meaning to a person's belief in it.
Figure 10 charts the progress of inquiry in this example according to the three stages of reasoning identified by Peirce.
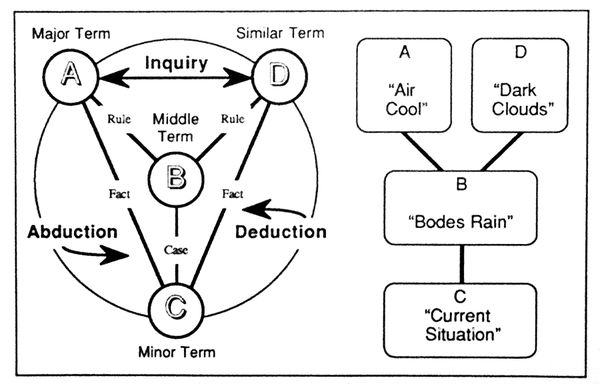
|
| \(\text{Figure 10. The Cycle of Inquiry}\!\) |
- Abduction. The first, faltering step into the cycle of inquiry is taken through the flexion of abductive reasoning. The fact C ⇒ A, the coolness of the air in the pedestrian's current situation, brings into play from his worldly experience (or from other kinds of background knowledge) the rule B ⇒ A, that a chill in the air is a feature of situations that betoken rain. This fact and this rule, working in tandem, precipitate a plausible explanation for the observed phenomena. The hiker abduces the case C ⇒ B, that bodes for rain in the current situation.
- Deduction. …
- Induction. …
In this analysis of the first steps of Inquiry, we have a complex or a mixed form of inference that can be seen as taking place in two steps:
1. The first step is an Abduction that abstracts a Case from the consideration of a Fact and a Rule.
| Fact: | C ⇒ A, | In the Current situation the Air is cool. | |
| Rule: | B ⇒ A, | Just Before it rains, the Air is cool. | |
| Case: | C ⇒ B, | The Current situation is just Before it rains. |
2. The final step is a Deduction that admits this Case to another Rule and so arrives at a novel Fact.
| Case: | C ⇒ B, | The Current situation is just Before it rains. | |
| Rule: | B ⇒ D, | Just Before it rains, a Dark cloud will appear. | |
| Fact: | C ⇒ D, | In the Current situation, a Dark cloud will appear. |
This is nowhere near a complete analysis of the Rainy Day inquiry, even insofar as it might be carried out within the constraints of the syllogistic framework, and it covers only the first two steps of the relevant inquiry process, but maybe it will do for a start.
2. Functional Conception of Quantification Theory
Up till now quantification theory has been based on the assumption of individual variables ranging over universal collections of perfectly determinate elements. Merely to write down quantified formulas like \(\forall_{x \in X} f(x)\!\) and \(\exists_{x \in X} f(x)\!\) involves a subscription to such notions, as shown by the membership relations invoked in their indices. Reflected on pragmatic and constructive principles, however, these ideas begin to appear as problematic hypotheses whose warrants are not beyond question, projects of exhaustive determination that overreach the powers of finite information and control to manage. Therefore, it is worth considering how we might shift the scene of quantification theory closer to familiar ground, toward the predicates themselves that represent our continuing acquaintance with phenomena.
Higher Order Propositional Expressions
By way of equipping this inquiry with a bit of concrete material, I begin with a consideration of higher order propositional expressions, in particular, those that stem from the propositions on 1 and 2 variables.
Higher Order Propositions and Logical Operators (n = 1)
A higher order proposition is, very roughly speaking, a proposition about propositions. If the original order of propositions is a class of indicator functions \({f : X \to \mathbb{B}},\!\) then the next higher order of propositions consists of maps of the type \({m : (X \to \mathbb{B}) \to \mathbb{B}}.\!\)
For example, consider the case where \({X = \mathbb{B}}.\!\) Then there are exactly four propositions \({f : \mathbb{B} \to \mathbb{B}},\!\) and exactly sixteen higher order propositions that are based on this set, all bearing the type \({m : (\mathbb{B} \to \mathbb{B}) \to \mathbb{B}}.\!\)
Table 11 lists the sixteen higher order propositions about propositions on one boolean variable, organized in the following fashion: Columns 1 and 2 form a truth table for the four \({f : \mathbb{B} \to \mathbb{B}},\!\) turned on its side from the way that one is most likely accustomed to see truth tables, with the row leaders in Column 1 displaying the names of the functions \({f_i},\!\) for \({i}\!\) = 1 to 4, while the entries in Column 2 give the values of each function for the argument values that are listed in the corresponding column head. Column 3 displays one of the more usual expressions for the proposition in question. The last sixteen columns are topped by a collection of conventional names for the higher order propositions, also known as the measures \({m_j},\!\) for \({j}\!\) = 0 to 15, where the entries in the body of the Table record the values that each \({m_j}\!\) assigns to each \({f_i}.\!\)
| \(x:\!\) | 1 0 | \(f\!\) | \(m_0\!\) | \(m_1\!\) | \(m_2\!\) | \(m_3\!\) | \(m_4\!\) | \(m_5\!\) | \(m_6\!\) | \(m_7\!\) | \(m_8\!\) | \(m_9\!\) | \(m_{10}\!\) | \(m_{11}\!\) | \(m_{12}\!\) | \(m_{13}\!\) | \(m_{14}\!\) | \(m_{15}\!\) |
| \(f_0\!\) | 0 0 | \(0\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_1\!\) | 0 1 | \(\texttt{(} x \texttt{)}\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_2\!\) | 1 0 | \(x\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_3\!\) | 1 1 | \(1\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
I am going to put off explaining Table 12, that presents a sample of what I call interpretive categories for higher order propositions, until after we get beyond the 1-dimensional case, since these lower dimensional cases tend to be a bit condensed or degenerate in their structures, and a lot of what is going on here will almost automatically become clearer as soon as we get even two logical variables into the mix.
| Measure | Happening | Exactness | Existence | Linearity | Uniformity | Information |
| \(m_0\!\) | Nothing happens | |||||
| \(m_1\!\) | Just false | Nothing exists | ||||
| \(m_2\!\) | Just not \(x\!\) | |||||
| \(m_3\!\) | Nothing is \(x\!\) | |||||
| \(m_4\!\) | Just \(x\!\) | |||||
| \(m_5\!\) | Everything is \(x\!\) | \(f\!\) is linear | ||||
| \(m_6\!\) | \(f\!\) is not uniform | \(f\!\) is informed | ||||
| \(m_7\!\) | Not just true | |||||
| \(m_8\!\) | Just true | |||||
| \(m_9\!\) | \(f\!\) is uniform | \(f\!\) is not informed | ||||
| \(m_{10}\!\) | Something is not \(x\!\) | \(f\!\) is not linear | ||||
| \(m_{11}\!\) | Not just \(x\!\) | |||||
| \(m_{12}\!\) | Something is \(x\!\) | |||||
| \(m_{13}\!\) | Not just not \(x\!\) | |||||
| \(m_{14}\!\) | Not just false | Something exists | ||||
| \(m_{15}\!\) | Anything happens |
Higher Order Propositions and Logical Operators (n = 2)
By way of reviewing notation and preparing to extend it to higher order universes of discourse, let us first consider the universe of discourse \(X^\bullet = [\mathcal{X}] = [x_1, x_2] = [u, v],\!\) based on two logical features or boolean variables \({u}\!\) and \({v}.\!\)
The universe of discourse \({X^\bullet}\!\) consists of two parts, a set of points and a set of propositions.
The points of \({X^\bullet}\!\) form the space:
| \({X \quad = \quad \langle \mathcal{X} \rangle \quad = \quad \langle u, v \rangle \quad = \quad \{ (u, v) \} \quad \cong \quad \mathbb{B}^2}.~\!\) |
Each point in \({X}\!\) may be indicated by means of a singular proposition, that is, a proposition that describes it uniquely. This form of representation leads to the following enumeration of points:
| \(X\!\) | \(=\!\) | \(\{ ~ \texttt{(} u \texttt{)(} v \texttt{)} ~,~ \texttt{(} u \texttt{)} ~ v ~,~ u ~ \texttt{(} v \texttt{)} ~,~ u ~ v ~ \}\!\) | \(\cong\!\) | \(\mathbb{B}^2,\!\) |
Each point in \(X\!\) may also be described by means of its coordinates, that is, by the ordered pair of values in \(\mathbb{B}\!\) that the coordinate propositions \(u\!\) and \(v\!\) take on that point. This form of representation leads to the following enumeration of points:
| \(X\!\) | \(=\!\) | \(\{\ (0, 0),\ (0, 1),\ (1, 0),\ (1, 1)\ \}\!\) | \(\cong\!\) | \(\mathbb{B}^2.\!\) |
The propositions of \({X^\bullet}\!\) form the space:
| \(X^\uparrow \quad = \quad (X \to \mathbb{B}) \quad = \quad \{ f : X \to \mathbb{B} \} \quad \cong \quad (\mathbb{B}^2 \to \mathbb{B}).\!\) |
As always, it is frequently convenient to omit a few of the finer markings of distinctions among isomorphic structures, so long as one is aware of their presence and knows when it is crucial to call upon them again.
The next higher order universe of discourse that is built on \({X^\bullet}\!\) is \(X^{\bullet 2} = [X^\bullet] = [[u, v]],\!\) which may be developed in the following way. The propositions of \({X^\bullet}\!\) become the points of \(X^{\bullet 2},\!\) and the mappings of the type \(m : (X \to \mathbb{B}) \to \mathbb{B}\!\) become the propositions of \(X^{\bullet 2}.\!\) In addition, it is convenient to equip the discussion with a selected set of higher order operators on propositions, all of which have the form \(w : (\mathbb{B}^2 \to \mathbb{B})^k \to \mathbb{B}.\!\)
To save a few words in the remainder of this discussion, I will use the terms measure and qualifier to refer to all types of higher order propositions and operators. To describe the present setting in picturesque terms, the propositions of \([u, v]\!\) may be regarded as a gallery of sixteen venn diagrams, while the measures \(m : (X \to \mathbb{B}) \to \mathbb{B}\!\) are analogous to a body of judges or a panel of critical viewers, each of whom evaluates each of the pictures as a whole and reports the ones that find favor or not. In this way, each judge \(m_j\!\) partitions the gallery of pictures into two aesthetic portions, the pictures \(m_j^{-1}(1)\!\) that \(m_j\!\) likes and the pictures \(m_j^{-1}(0)\!\) that \(m_j\!\) dislikes.
There are \(2^{16} = 65536\!\) measures of the type \(m : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}.\!\) Table 13 introduces the first 24 of these measures in the fashion of the higher order truth table that I used before. The column headed \(m_j\!\) shows the values of the measure \(m_j\!\) on each of the propositions \(f_i : \mathbb{B}^2 \to \mathbb{B},\!\) for \(i\!\) = 0 to 23, with blank entries in the Table being optional for values of zero. The arrangement of measures that continues according to the plan indicated here is referred to as the standard ordering of these measures. In this scheme of things, the index \(j\!\) of the measure \(m_j\!\) is the decimal equivalent of the bit string that is associated with \(m_j\!\)'s functional values, which can be obtained in turn by reading the \(j^\mathrm{th}\!\) column of binary digits in the Table as the corresponding range of boolean values, taking them up in the order from bottom to top.
| \(\begin{matrix}u\!:\\v\!:\end{matrix}\) | \(\begin{matrix}1100\\1010\end{matrix}\) | \(f\!\) | \({\underset{0}{m}}\!\) | \({\underset{1}{m}}\!\) | \({\underset{2}{m}}\!\) | \({\underset{3}{m}}\!\) | \({\underset{4}{m}}\!\) | \({\underset{5}{m}}\!\) | \({\underset{6}{m}}\!\) | \({\underset{7}{m}}\!\) | \({\underset{8}{m}}\!\) | \({\underset{9}{m}}\!\) | \({\underset{10}{m}}\!\) | \({\underset{11}{m}}\!\) | \({\underset{12}{m}}\!\) | \({\underset{13}{m}}\!\) | \({\underset{14}{m}}\!\) | \({\underset{15}{m}}\!\) | \({\underset{16}{m}}\!\) | \({\underset{17}{m}}\!\) | \({\underset{18}{m}}\!\) | \({\underset{19}{m}}\!\) | \({\underset{20}{m}}\!\) | \({\underset{21}{m}}\!\) | \({\underset{22}{m}}\!\) | \({\underset{23}{m}}\!\) |
| \(f_0\!\) | \(0000\!\) | \(\texttt{(~)}\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_1\!\) | \(0001\!\) | \(\texttt{(u)(v)}\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_2\!\) | \({0010}\!\) | \(\texttt{(u) v}\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_3\!\) | \(0011\!\) | \(\texttt{(u)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_4\!\) | \(0100\!\) | \(\texttt{u (v)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(f_5\!\) | \({0101}\!\) | \(\texttt{(v)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_6\!\) | \(0110\!\) | \(\texttt{(u, v)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_7\!\) | \(0111\!\) | \(\texttt{(u v)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_8\!\) | \(1000\!\) | \(\texttt{u v}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_9\!\) | \(1001\!\) | \(\texttt{((u, v))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{10}\!\) | \(1010\!\) | \(\texttt{v}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{11}\!\) | \(1011\!\) | \(\texttt{(u (v))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{12}\!\) | \(1100\!\) | \(\texttt{u}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{13}\!\) | \(1101\!\) | \(\texttt{((u) v)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{14}\!\) | \(1110\!\) | \(\texttt{((u)(v))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{15}\!\) | \(1111\!\) | \(\texttt{((~))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Umpire Operators
We now examine measures at the high end of the standard ordering. Instrumental to this purpose we define a couple of higher order operators, \(\Upsilon_1 : (\langle u, v \rangle \to \mathbb{B}) \to \mathbb{B}\!\) and \(\Upsilon : (\langle u, v \rangle \to \mathbb{B})^2 \to \mathbb{B},\!\) both symbolized by cursive upsilon characters and referred to as the absolute and relative umpire operators, respectively. If either one of these operators is defined in terms of more primitive notions then the remaining operator can be defined in terms of the one first established.
Given an ordered pair of propositions \(e, f : \langle u, v \rangle \to \mathbb{B}\!\) as arguments, the relative operator reports the value \(1\!\) if the first implies the second, otherwise \(0.\!\)
| \(\Upsilon (e, f) = 1\!\) | \(\operatorname{if~and~only~if}\!\) | \(e \Rightarrow f.\!\) |
To express it another way:
| \(\Upsilon (e, f) = 1\!\) | \(\iff\!\) | \(\texttt{(} e \texttt{(} f \texttt{))} = 1\!\) |
In writing this, however, it is important to notice that the \(1\!\) appearing on the left side and the \(1\!\) appearing on the right side of the logical equivalence have different meanings. Filling in the details, we have:
| \(\Upsilon (e, f) = 1 \in \mathbb{B}\!\) | \(\iff\!\) | \(\texttt{(} e \texttt{(} f \texttt{))} = 1 : \langle u, v \rangle \to \mathbb{B}\!\) |
Writing types as subscripts and using the fact that \(X = \langle u, v \rangle,\!\) it is possible to express this a little more succinctly as follows:
| \(\Upsilon (e, f) = 1_\mathbb{B}\!\) | \(\iff\!\) | \(\texttt{(} e \texttt{(} f \texttt{))} = 1_{X \to \mathbb{B}}\!\) |
Finally, it is often convenient to write the first argument as a subscript, hence \(\Upsilon_e (f) = \Upsilon (e, f).\!\)
As a special application of this operator, we next define the absolute umpire operator, also called the umpire measure. This is a higher order proposition \(\Upsilon_1 : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}\!\) which is given by the relation \(\Upsilon_1 (f) = \Upsilon (1, f).\!\) Here, the subscript \(1\!\) on the left and the argument \(1\!\) on the right both refer to the constant proposition \(1 : \mathbb{B}^2 \to \mathbb{B}.\!\) In most contexts where \(\Upsilon_1\!\) is actually applied the subscript \(1\!\) is safely omitted, since the number of arguments indicates which type of operator is intended. Thus, we have the following identities and equivalents:
| \(\Upsilon f = \Upsilon_1 (f) = 1 \in \mathbb{B}\!\) | \(\iff\!\) | \(\texttt{(} 1 ~ \texttt{(} f \texttt{))} = 1\!\) | \(\iff\!\) | \(f = 1 : \mathbb{B}^2 \to \mathbb{B}\!\) |
The umpire measure is defined at the level of truth functions, but can also be understood in terms of its implied judgments at the syntactic level. Interpreted this way, \(\Upsilon_1\!\) recognizes theorems of the propositional calculus over \([u, v],\!\) giving a score of \(1\!\) to tautologies and a score of \(0\!\) to everything else, regarding all contingent statements as no better than falsehoods.
One remark in passing for those who might prefer an alternative definition. If we had originally taken \(\Upsilon\!\) to mean the absolute measure, then the relative version could have been defined as \(\Upsilon_e f = \Upsilon \texttt{(} e \texttt{(} f \texttt{))}.~\!\)
Measure for Measure
Define two families of measures:
| \(\alpha_i, \beta_i : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}, i = 0 \ldots 15,\!\) |
by means of the following formulas:
| \(\alpha_i f = \Upsilon (f_i, f) = \Upsilon (f_i \Rightarrow f),\!\) |
| \(\beta_i f = \Upsilon (f, f_i) = \Upsilon (f \Rightarrow f_i).\!\) |
The values of the sixteen \(\alpha_i\!\) on each of the sixteen boolean functions \(f : \mathbb{B}^2 \to \mathbb{B}\!\) are shown in Table 14. Expressed in terms of the implication ordering on the sixteen functions, \(\alpha_i f = 1\!\) says that \(f\!\) is above or identical to \(f_i\!\) in the implication lattice, that is, \(\ge f_i\!\) in the implication ordering.
| \(u:\!\) \(v:\!\) |
1100 1010 |
\(f\!\) | \(\alpha_0~\!\) | \(\alpha_1\!\) | \(\alpha_2\!\) | \(\alpha_3\!\) | \(\alpha_4\!\) | \(\alpha_5\!\) | \(\alpha_6\!\) | \(\alpha_7\!\) | \(\alpha_8\!\) | \(\alpha_9\!\) | \(\alpha_{10}\!\) | \(\alpha_{11}\!\) | \(\alpha_{12}\!\) | \(\alpha_{13}~\!\) | \(\alpha_{14}\!\) | \(\alpha_{15}\!\) |
| \(f_0\!\) | 0000 | \(\texttt{(~)}\!\) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_1\!\) | 0001 | \(\texttt{(} u \texttt{)(} v \texttt{)}\!\) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_2\!\) | 0010 | \(\texttt{(} u \texttt{)} ~ v\!\) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_3\!\) | 0011 | \(\texttt{(} u \texttt{)}~\!\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_4\!\) | 0100 | \(u ~ \texttt{(} v \texttt{)}\!\) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_5\!\) | 0101 | \(\texttt{(} v \texttt{)}\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_6\!\) | 0110 | \(\texttt{(} u ~ \texttt{,} ~ v \texttt{)}\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_7\!\) | 0111 | \(\texttt{(} u ~ v \texttt{)}\!\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_8\!\) | 1000 | \(u ~ v\!\) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_9\!\) | 1001 | \(\texttt{((} u ~ \texttt{,} ~ v \texttt{))}\!\) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{10}\!\) | 1010 | \(v\!\) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| \(f_{11}\!\) | 1011 | \(\texttt{(} u ~ \texttt{(} v \texttt{))}\!\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| \(f_{12}\!\) | 1100 | \(u\!\) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| \(f_{13}\!\) | 1101 | \(\texttt{((} u \texttt{)} ~ v \texttt{)}\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| \(f_{14}\!\) | 1110 | \(\texttt{((} u \texttt{)(} v \texttt{))}\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(f_{15}\!\) | 1111 | \(\texttt{((~))}\!\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
The values of the sixteen \({\beta_i}\!\) on each of the sixteen boolean functions \({f : \mathbb{B}^2 \to \mathbb{B}}\!\) are shown in Table 15. Expressed in terms of the implication ordering on the sixteen functions, \({\beta_i f = 1}\!\) says that \({f}\!\) is below or identical to \({f_i}\!\) in the implication lattice, that is, \({\le f_i}\!\) in the implication ordering.
| \(u:\!\) \(v:\!\) |
1100 1010 |
\(f\!\) | \(\beta_0\!\) | \(\beta_1\!\) | \(\beta_2\!\) | \(\beta_3\!\) | \(\beta_4\!\) | \(\beta_5\!\) | \(\beta_6\!\) | \(\beta_7\!\) | \(\beta_8\!\) | \(\beta_9\!\) | \(\beta_{10}\!\) | \(\beta_{11}\!\) | \(\beta_{12}\!\) | \(\beta_{13}\!\) | \(\beta_{14}\!\) | \(\beta_{15}\!\) |
| \(f_0\!\) | 0000 | \(\texttt{(~)}\!\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(f_1\!\) | 0001 | \(\texttt{(} u \texttt{)(} v \texttt{)}\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_2\!\) | 0010 | \(\texttt{(} u \texttt{)} ~ v\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_3\!\) | 0011 | \(\texttt{(} u \texttt{)}~\!\) | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| \(f_4\!\) | 0100 | \(u ~ \texttt{(} v \texttt{)}\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_5\!\) | 0101 | \(\texttt{(} v \texttt{)}\!\) | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| \(f_6\!\) | 0110 | \(\texttt{(} u ~ \texttt{,} ~ v \texttt{)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| \(f_7\!\) | 0111 | \(\texttt{(} u ~ v \texttt{)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| \(f_8\!\) | 1000 | \(u ~ v\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(f_9\!\) | 1001 | \(\texttt{((} u ~ \texttt{,} ~ v \texttt{))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_{10}\!\) | 1010 | \(v\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_{11}\!\) | 1011 | \(\texttt{(} u ~ \texttt{(} v \texttt{))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| \(f_{12}\!\) | 1100 | \(u\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_{13}\!\) | 1101 | \(\texttt{((} u \texttt{)} ~ v \texttt{)}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| \(f_{14}\!\) | 1110 | \(\texttt{((} u \texttt{)(} v \texttt{))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| \(f_{15}\!\) | 1111 | \(\texttt{((~))}\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Applied to a given proposition \(f,\!\) the qualifiers \(\alpha_i\!\) and \(\beta_i\!\) tell whether \(f\!\) rests \(\operatorname{above}\ f_i\!\) or \(\operatorname{below}\ f_i,\!\) respectively, in the implication ordering. By way of example, let us trace the effects of several such measures, namely, those that occupy the limiting positions of the Tables.
|
\(\begin{array}{rclrrrrr} \alpha_0 f = 1 & \text{iff} & f_0 \Rightarrow f & \text{iff} & 0 \Rightarrow f, & \text{hence} & \alpha_0 f = 1 & \text{for all}~ f. \\ \alpha_{15} f = 1 & \text{iff} & f_{15} \Rightarrow f & \text{iff} & 1 \Rightarrow f, & \text{hence} & \alpha_{15} f = 1 & \text{iff}~ f = 1. \\ \beta_0 f = 1 & \text{iff} & f \Rightarrow f_0 & \text{iff} & f \Rightarrow 0, & \text{hence} & \beta_0 f = 1 & \text{iff}~ f = 0. \\ \beta_{15} f = 1 & \text{iff} & f \Rightarrow f_{15} & \text{iff} & f \Rightarrow 1, & \text{hence} & \beta_{15} f = 1 & \text{for all}~ f. \end{array}\) |
Thus, \(\alpha_0 = \beta_{15}\!\) is a totally indiscriminate measure, one that accepts all propositions \({f : \mathbb{B}^2 \to \mathbb{B}},\!\) whereas \(\alpha_{15}\!\) and \(\beta_0\!\) are measures that value the constant propositions \(1 : \mathbb{B}^2 \to \mathbb{B}\!\) and \(0 : \mathbb{B}^2 \to \mathbb{B},\!\) respectively, above all others.
Finally, in conformity with the use of the fiber notation to indicate sets of models, it is natural to use notations like:
| \([| \alpha_i |]\!\) | \(=\!\) | \((\alpha_i)^{-1}(1),\!\) |
| \([| \beta_i |]\!\) | \(=\!\) | \((\beta_i)^{-1}(1),\!\) |
| \([| \Upsilon_p |]\!\) | \(=\!\) | \((\Upsilon_p)^{-1}(1),\!\) |
to denote sets of propositions that satisfy the umpires in question.
Extending the Existential Interpretation to Quantificational Logic
Previously I introduced a calculus for propositional logic, fixing its meaning according to what C.S. Peirce called the existential interpretation. As far as it concerns propositional calculus this interpretation settles the meanings that are associated with merely the most basic symbols and logical connectives. Now we must extend and refine the existential interpretation to comprehend the analysis of quantifications, that is, quantified propositions. In doing so we recognize two additional aspects of logic that need to be developed, over and above the material of propositional logic. At the formal extreme there is the aspect of higher order functional types, into which we have already ventured a little above. At the level of the fundamental content of the available propositions we have to introduce a different interpretation for what we may call elemental or singular propositions.
Let us return to the 2-dimensional case \(X^\bullet = [u, v].\!\) In order to provide a bridge between propositions and quantifications it serves to define a set of qualifiers \(\ell_{ij} : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}\!\) that have the following characters:
Intuitively, the \(\ell_{ij}\!\) operators may be thought of as qualifying propositions according to the elements of the universe of discourse that each proposition positively values. Taken together, these measures provide us with the means to express many useful observations about the propositions in \(X^\bullet = [u, v],\!\) and so they mediate a subtext \([\ell_{00}, \ell_{01}, \ell_{10}, \ell_{11}]\!\) that takes place within the higher order universe of discourse \(X^{\bullet 2} = [X^\bullet] = [[u, v]].\!\) Figure 16 summarizes the action of the \(\ell_{ij}\!\) operators on the \(f_i\!\) within \(X^{\bullet 2}.\!\)
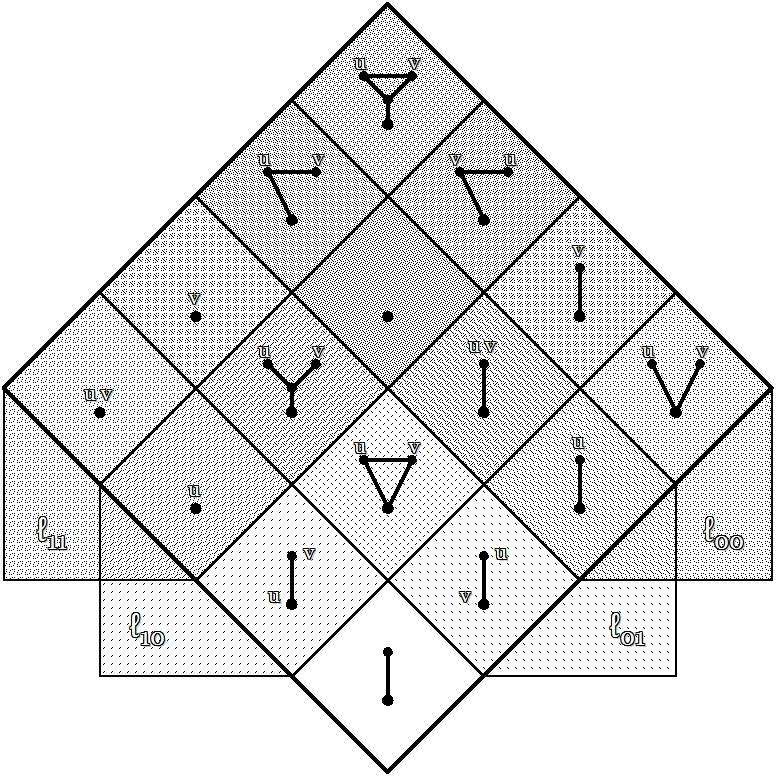
|
| \(\text{Figure 16.} ~~ \text{Higher Order Universe of Discourse} ~ \left[ \ell_{00}, \ell_{01}, \ell_{10}, \ell_{11} \right] \subseteq \left[\left[ u, v \right]\right]\!\) |
Application of Higher Order Propositions to Quantification Theory
Our excursion into the vastening landscape of higher order propositions has finally come round to the stage where we can bring its returns to bear on opening up new perspectives for quantificational logic.
There is a question arising next that is still experimental in my mind. Whether it makes much difference from a purely formal point of view is not a question I can answer yet, but it does seem to aid the intuition to invent a slightly different interpretation for the two-valued space that we use as the target of our basic indicator functions. Therefore, let us declare a type of existential-valued functions \(f : \mathbb{B}^k \to \mathbb{E},\!\) where \(\mathbb{E} = \{ -e, +e \} = \{ \operatorname{empty}, \operatorname{exist} \}\!\) is a couple of values that we interpret as indicating whether of not anything exists in the cells of the underlying universe of discourse, venn diagram, or other domain. As usual, let us not be too strict about the coding of these functions, reverting to binary codes whenever the interpretation is clear enough.
With this interpretation in mind we note the following correspondences between classical quantifications and higher order indicator functions:
|
\(\begin{array}{clcl} \mathrm{A} & \mathrm{Universal~Affirmative} & \mathrm{All}\ u\ \mathrm{is}\ v & \mathrm{Indicator~of}\ u (v) = 0 \\ \mathrm{E} & \mathrm{Universal~Negative} & \mathrm{All}\ u\ \mathrm{is}\ (v) & \mathrm{Indicator~of}\ u \cdot v = 0 \\ \mathrm{I} & \mathrm{Particular~Affirmative} & \mathrm{Some}\ u\ \mathrm{is}\ v & \mathrm{Indicator~of}\ u \cdot v = 1 \\ \mathrm{O} & \mathrm{Particular~Negative} & \mathrm{Some}\ u\ \mathrm{is}\ (v) & \mathrm{Indicator~of}\ u (v) = 1 \\ \end{array}\) |
The following Tables develop these ideas in more detail.
| \(u:\!\) \(v:\!\) |
1100 1010 |
\(f\!\) | \((\ell_{11})\!\) \(\text{No } u \!\) \(\text{is } v \!\) |
\((\ell_{10})\!\) \(\text{No } u \!\) \(\text{is }(v)\!\) |
\((\ell_{01})\!\) \(\text{No }(u)\!\) \(\text{is } v \!\) |
\((\ell_{00})\!\) \(\text{No }(u)\!\) \(\text{is }(v)\!\) |
\( \ell_{00} \!\) \(\text{Some }(u)\!\) \(\text{is }(v)\!\) |
\( \ell_{01} \!\) \(\text{Some }(u)\!\) \(\text{is } v \!\) |
\( \ell_{10}~\!\) \(\text{Some } u \!\) \(\text{is }(v)\!\) |
\( \ell_{11} \!\) \(\text{Some } u \!\) \(\text{is } v \!\) |
| \(f_0\!\) | 0000 | \((~)\!\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| \(f_1\!\) | 0001 | \((u)(v)\!\) | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| \(f_2\!\) | 0010 | \((u) v\!\) | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| \(f_3\!\) | 0011 | \((u)~\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| \(f_4\!\) | 0100 | \(u (v)\!\) | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| \(f_5\!\) | 0101 | \((v)\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(f_6\!\) | 0110 | \((u, v)\!\) | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| \(f_7\!\) | 0111 | \((u v)\!\) | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| \(f_8\!\) | 1000 | \(u v\!\) | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| \(f_9\!\) | 1001 | \(((u, v))\!\) | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| \(f_{10}\!\) | 1010 | \(v\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_{11}\!\) | 1011 | \((u (v))\!\) | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| \(f_{12}\!\) | 1100 | \(u\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_{13}\!\) | 1101 | \(((u) v)\!\) | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| \(f_{14}\!\) | 1110 | \(((u)(v))~\!\) | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| \(f_{15}\!\) | 1111 | \(((~))\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(u:\!\) \(v:\!\) |
1100 1010 |
\(f\!\) | \((\ell_{11})\!\) \(\text{No } u \!\) \(\text{is } v \!\) |
\((\ell_{10})\!\) \(\text{No } u \!\) \(\text{is }(v)\!\) |
\((\ell_{01})\!\) \(\text{No }(u)\!\) \(\text{is } v \!\) |
\((\ell_{00})\!\) \(\text{No }(u)\!\) \(\text{is }(v)\!\) |
\( \ell_{00} \!\) \(\text{Some }(u)\!\) \(\text{is }(v)\!\) |
\( \ell_{01} \!\) \(\text{Some }(u)\!\) \(\text{is } v \!\) |
\( \ell_{10}~\!\) \(\text{Some } u \!\) \(\text{is }(v)\!\) |
\( \ell_{11} \!\) \(\text{Some } u \!\) \(\text{is } v \!\) |
| \(f_0\!\) | 0000 | \((~)\!\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| \(f_1\!\) | 0001 | \((u)(v)\!\) | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| \(f_2\!\) | 0010 | \((u) v\!\) | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| \(f_4\!\) | 0100 | \(u (v)\!\) | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| \(f_8\!\) | 1000 | \(u v\!\) | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| \(f_3\!\) | 0011 | \((u)~\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| \(f_{12}\!\) | 1100 | \(u\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_6\!\) | 0110 | \((u, v)\!\) | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| \(f_9\!\) | 1001 | \(((u, v))\!\) | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| \(f_5\!\) | 0101 | \((v)\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(f_{10}\!\) | 1010 | \(v\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_7\!\) | 0111 | \((u v)\!\) | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| \(f_{11}\!\) | 1011 | \((u (v))\!\) | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| \(f_{13}\!\) | 1101 | \(((u) v)\!\) | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| \(f_{14}\!\) | 1110 | \(((u)(v))~\!\) | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| \(f_{15}\!\) | 1111 | \(((~))\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(\text{Mnemonic}\!\) | \(\text{Category}\!\) | \(\text{Classical Form}\!\) | \(\text{Alternate Form}\!\) | \(\text{Symmetric Form}\!\) | \(\text{Operator}\!\) |
| \(\text{E}\!\) \(\text{Exclusive}\!\) |
\(\text{Universal}\!\) \(\text{Negative}\!\) |
\(\text{All}~ u ~\text{is}~ (v)\!\) | \(\text{No}~ u ~\text{is}~ v \!\) | \({(\ell_{11})}\!\) | |
| \(\text{A}\!\) \(\text{Absolute}~\!\) |
\(\text{Universal}\!\) \(\text{Affirmative}\!\) |
\(\text{All}~ u ~\text{is}~ v \!\) | \(\text{No}~ u ~\text{is}~ (v)\!\) | \({(\ell_{10})}\!\) | |
| \(\text{All}~ v ~\text{is}~ u \!\) | \(\text{No}~ v ~\text{is}~ (u)\!\) | \(\text{No}~ (u) ~\text{is}~ v \!\) | \({(\ell_{01})}\!\) | ||
| \(\text{All}~ (v) ~\text{is}~ u \!\) | \(\text{No}~ (v) ~\text{is}~ (u)\!\) | \(\text{No}~ (u) ~\text{is}~ (v)\!\) | \({(\ell_{00})}\!\) | ||
| \(\text{Some}~ (u) ~\text{is}~ (v)\!\) | \(\text{Some}~ (u) ~\text{is}~ (v)\!\) | \({\ell_{00}}\!\) | |||
| \(\text{Some}~ (u) ~\text{is}~ v\!\) | \(\text{Some}~ (u) ~\text{is}~ v\!\) | \({\ell_{01}}\!\) | |||
| \(\text{O}\!\) \(\text{Obtrusive}\!\) |
\(\text{Particular}\!\) \(\text{Negative}\!\) |
\(\text{Some}~ u ~\text{is}~ (v)\!\) | \(\text{Some}~ u ~\text{is}~ (v)\!\) | \({\ell_{10}}\!\) | |
| \(\text{I}\!\) \(\text{Indefinite}\!\) |
\(\text{Particular}\!\) \(\text{Affirmative}\!\) |
\(\text{Some}~ u ~\text{is}~ v\!\) | \(\text{Some}~ u ~\text{is}~ v\!\) | \({\ell_{11}}\!\) |
Appendix : Generalized Umpire Operators
In order to get a handle on the space of higher order propositions and eventually to carry out a functional approach to quantification theory, it serves to construct some specialized tools. Specifically, I define a higher order operator \(\Upsilon,\!\) called the umpire operator, which takes up to three propositions as arguments and returns a single truth value as the result. Formally, this so-called multi-grade property of \(\Upsilon\!\) can be expressed as a union of function types, in the following manner:
| \(\Upsilon : \bigcup_{\ell = 1, 2, 3} ((\mathbb{B}^k \to \mathbb{B})^\ell \to \mathbb{B}).\!\) |
In contexts of application the intended sense can be discerned by the number of arguments that actually appear in the argument list. Often, the first and last arguments appear as indices, the one in the middle being treated as the main argument while the other two arguments serve to modify the sense of the operation in question. Thus, we have the following forms:
| \(\Upsilon_p^r q = \Upsilon (p, q, r)\!\) |
| \(\Upsilon_p^r : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}\!\) |
The intention of this operator is that we evaluate the proposition \(q\!\) on each model of the proposition \(p\!\) and combine the results according to the method indicated by the connective parameter \(r.\!\) In principle, the index \(r\!\) might specify any connective on as many as \(2^k\!\) arguments, but usually we have in mind a much simpler form of combination, most often either collective products or collective sums. By convention, each of the accessory indices \(p, r\!\) is assigned a default value that is understood to be in force when the corresponding argument place is left blank, specifically, the constant proposition \(1 : \mathbb{B}^k \to \mathbb{B}\!\) for the lower index \(p,\!\) and the continued conjunction or continued product operation \(\textstyle\prod\!\) for the upper index \(r.\!\) Taking the upper default value gives license to the following readings:
| \(\Upsilon_p (q) = \Upsilon (p, q) = \Upsilon (p, q, \textstyle\prod).\!\) |
| \(\Upsilon_p = \Upsilon (p, \underline{~~}, \textstyle\prod) : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}.\!\) |
This means that \(\Upsilon_p (q) = 1\!\) if and only if \(q\!\) holds for all models of \(p.\!\) In propositional terms, this is tantamount to the assertion that \(p \Rightarrow q,\!\) or that \(\underline{(p (q))} = \underline{1}.\!\)
Throwing in the lower default value permits the following abbreviations:
| \(\Upsilon q = \Upsilon (q) = \Upsilon_1 (q) = \Upsilon (1, q, \textstyle\prod).\!\) |
| \(\Upsilon = \Upsilon (1, \underline{~~}, \textstyle\prod)) : (\mathbb{B}^k\ \to \mathbb{B}) \to \mathbb{B}.\!\) |
This means that \(\Upsilon q = 1\!\) if and only if \(q\!\) holds for the whole universe of discourse in question, that is, if and only \(q\!\) is the constantly true proposition \(1 : \mathbb{B}^k \to \mathbb{B}.\!\) The ambiguities of this usage are not a problem so long as we distinguish the context of definition from the context of application and restrict all shorthand notations to the latter.
References
- Aristotle, “Prior Analytics”, Hugh Tredennick (trans.), in Aristotle, Volume 1, Loeb Classical Library, William Heinemann, London, UK, 1938.
Document History
Inquiry and Analogy
| Author: | Jon Awbrey | November 1, 1995 |
| Course: | Engineering 690, Graduate Project | Winter Term, January 1995 |
| Supervisors: | M.A. Zohdy and F. Mili | Oakland University |
| Version: Draft 3.25 | Created: 01 Jan 1995 | Relayed: 01 Nov 1995 | Revised: 24 Dec 2001 | Revised: 12 Mar 2004
Functional Logic
Inquiry List
- http://web.archive.org/web/20090303000827/http://stderr.org/pipermail/inquiry/2004-March/001256.html
- http://web.archive.org/web/20090303001935/http://stderr.org/pipermail/inquiry/2004-March/001257.html
- http://web.archive.org/web/20090303002148/http://stderr.org/pipermail/inquiry/2004-March/001258.html
- http://web.archive.org/web/20090303001240/http://stderr.org/pipermail/inquiry/2004-March/001259.html
- http://web.archive.org/web/20090303001940/http://stderr.org/pipermail/inquiry/2004-March/001260.html
- http://web.archive.org/web/20090303002026/http://stderr.org/pipermail/inquiry/2004-March/001261.html
Ontology List
- http://web.archive.org/web/20090303202815/http://suo.ieee.org/ontology/msg05480.html
- http://web.archive.org/web/20090302145522/http://suo.ieee.org/ontology/msg05481.html
- http://web.archive.org/web/20090302145531/http://suo.ieee.org/ontology/msg05482.html
- http://web.archive.org/web/20090303203051/http://suo.ieee.org/ontology/msg05483.html
- http://web.archive.org/web/20090303203442/http://suo.ieee.org/ontology/msg05484.html
- http://web.archive.org/web/20090302145538/http://suo.ieee.org/ontology/msg05485.html
NKS Forum
- http://web.archive.org/web/20131120210604/http://forum.wolframscience.com/archive/topic/254.html
- http://web.archive.org/web/20090302144746/http://forum.wolframscience.com/showthread.php?threadid=254
Inquiry Driven Systems
NKS Forum
- http://web.archive.org/web/20131104033846/http://forum.wolframscience.com/archive/topic/598.html
- http://web.archive.org/web/20160406171418/http://forum.wolframscience.com/showthread.php?threadid=598
- http://web.archive.org/web/20090302150057/http://forum.wolframscience.com/showthread.php?postid=1957#post1957
- http://web.archive.org/web/20090302145607/http://forum.wolframscience.com/showthread.php?postid=1960#post1960
- http://web.archive.org/web/20090302150102/http://forum.wolframscience.com/showthread.php?postid=1961#post1961
- http://web.archive.org/web/20090302150134/http://forum.wolframscience.com/showthread.php?postid=1962#post1962
- http://web.archive.org/web/20090302145918/http://forum.wolframscience.com/showthread.php?postid=1964#post1964
- http://web.archive.org/web/20090302145303/http://forum.wolframscience.com/showthread.php?postid=1966#post1966
- http://web.archive.org/web/20090302150013/http://forum.wolframscience.com/showthread.php?postid=1968#post1968
- Adaptive Systems
- Artificial Intelligence
- Charles Sanders Peirce
- Combinatorics
- Computer Science
- Cybernetics
- Differential Logic
- Discrete Systems
- Dynamical Systems
- Formal Languages
- Formal Sciences
- Formal Systems
- Functional Logic
- Graph Theory
- Group Theory
- Inquiry
- Knowledge Representation
- Linguistics
- Logic
- Logical Graphs
- Mathematics
- Mathematical Systems Theory
- Science
- Semiotics
- Philosophy
- Systems Science
- Visualization