Difference between revisions of "Directory talk:Jon Awbrey/Papers/Peirce's 1870 Logic Of Relatives"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) (→Mathematical Demonstration and the Doctrine of Individuals: delete blog-formatted pieces) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''Author: [[User:Jon Awbrey|Jon Awbrey]]''' | '''Author: [[User:Jon Awbrey|Jon Awbrey]]''' | ||
| − | ' | + | Peirce's text employs lower case letters for logical terms of general reference and upper case letters for logical terms of individual reference. General terms fall into types — absolute terms, dyadic relative terms, higher adic relative terms — and Peirce employs different typefaces to distinguish these. The following Tables indicate the typefaces that are used in the text below for Peirce's examples of general terms. |
| − | + | <br> | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | |+ <math>\text{Absolute Terms (Monadic Relatives)}\!</math> | |
| − | + | | | |
| − | + | <math>\begin{array}{ll} | |
| − | + | \mathrm{a}. & \text{animal} | |
| − | + | \\ | |
| − | {| align="center" | + | \mathrm{b}. & \text{black} |
| − | | | + | \\ |
| + | \mathrm{f}. & \text{Frenchman} | ||
| + | \\ | ||
| + | \mathrm{h}. & \text{horse} | ||
| + | \\ | ||
| + | \mathrm{m}. & \text{man} | ||
| + | \\ | ||
| + | \mathrm{p}. & \text{President of the United States Senate} | ||
| + | \\ | ||
| + | \mathrm{r}. & \text{rich person} | ||
| + | \\ | ||
| + | \mathrm{u}. & \text{violinist} | ||
| + | \\ | ||
| + | \mathrm{v}. & \text{Vice-President of the United States} | ||
| + | \\ | ||
| + | \mathrm{w}. & \text{woman} | ||
| + | \end{array}</math> | ||
|} | |} | ||
| − | + | <br> | |
| − | |||
| − | |||
| − | {| align="center" | + | {| align="center" cellspacing="6" width="90%" |
| − | | | + | |+ <math>\text{Simple Relative Terms (Dyadic Relatives)}\!</math> |
| + | | | ||
| + | <math>\begin{array}{ll} | ||
| + | \mathit{a}. & \text{enemy} | ||
| + | \\ | ||
| + | \mathit{b}. & \text{benefactor} | ||
| + | \\ | ||
| + | \mathit{c}. & \text{conqueror} | ||
| + | \\ | ||
| + | \mathit{e}. & \text{emperor} | ||
| + | \\ | ||
| + | \mathit{h}. & \text{husband} | ||
| + | \\ | ||
| + | \mathit{l}. & \text{lover} | ||
| + | \\ | ||
| + | \mathit{m}. & \text{mother} | ||
| + | \\ | ||
| + | \mathit{n}. & \text{not} | ||
| + | \\ | ||
| + | \mathit{o}. & \text{owner} | ||
| + | \\ | ||
| + | \mathit{s}. & \text{servant} | ||
| + | \\ | ||
| + | \mathit{w}. & \text{wife} | ||
| + | \end{array}</math> | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
| − | {| align="center | + | {| align="center" cellspacing="6" width="90%" |
| − | |+ <math>\text{ | + | |+ <math>\text{Conjugative Terms (Higher Adic Relatives)}\!</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{ll} |
| − | + | \mathfrak{b}. & \text{betrayer to ------ of ------} | |
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\\ | \\ | ||
| − | \ | + | \mathfrak{g}. & \text{giver to ------ of ------} |
| − | |||
| − | |||
| − | |||
| − | & \ | ||
\\ | \\ | ||
| − | \ | + | \mathfrak{t}. & \text{transferrer from ------ to ------} |
\\ | \\ | ||
| − | \ | + | \mathfrak{w}. & \text{winner over of ------ to ------ from ------} |
| − | \end{ | + | \end{array}</math> |
| − | | | + | |} |
| − | + | ||
| − | + | <br> | |
| − | + | ||
| − | <math>\ | + | Individual terms are taken to denote individual entities falling under a general term. Peirce uses upper case Roman letters for individual terms, for example, the individual horses <math>\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}</math> falling under the general term <math>\mathrm{h}\!</math> for ''horse''. |
| − | \ | + | |
| − | + | The path to understanding Peirce's system and its wider implications for logic can be smoothed by paraphrasing his notations in a variety of contemporary mathematical formalisms, while preserving the semantics as much as possible. Remaining faithful to Peirce's orthography while adding parallel sets of stylistic conventions will, however, demand close attention to typography-in-context. Current style sheets for mathematical texts specify italics for mathematical variables, with upper case letters for sets and lower case letters for individuals. So we need to keep an eye out for the difference between the individual <math>\mathrm{X}\!</math> of the genus <math>\mathrm{x}\!</math> and the element <math>x\!</math> of the set <math>X\!</math> as we pass between the two styles of text. | |
| − | a, | + | |
| − | + | __TOC__ | |
| − | \mathrm{ | + | |
| − | \ | + | ==Selection 1== |
| − | \mathrm{ | + | |
| − | \\ | + | ===Use of the Letters=== |
| − | \ | + | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| | | | ||
| − | < | + | <p>The letters of the alphabet will denote logical signs.</p> |
| − | & a | + | |
| − | + | <p>Now logical terms are of three grand classes.</p> | |
| − | + | ||
| − | + | <p>The first embraces those whose logical form involves only the conception of quality, and which therefore represent a thing simply as “a ——”. These discriminate objects in the most rudimentary way, which does not involve any consciousness of discrimination. They regard an object as it is in itself as ''such'' (''quale''); for example, as horse, tree, or man. These are ''absolute terms''.</p> | |
| − | + | ||
| − | + | <p>The second class embraces terms whose logical form involves the conception of relation, and which require the addition of another term to complete the denotation. These discriminate objects with a distinct consciousness of discrimination. They regard an object as over against another, that is as relative; as father of, lover of, or servant of. These are ''simple relative terms''.</p> | |
| − | + | ||
| − | + | <p>The third class embraces terms whose logical form involves the conception of bringing things into relation, and which require the addition of more than one term to complete the denotation. They discriminate not only with consciousness of discrimination, but with consciousness of its origin. They regard an object as medium or third between two others, that is as conjugative; as giver of —— to ——, or buyer of —— for —— from ——. These may be termed ''conjugative terms''.</p> | |
| − | + | ||
| − | | | + | <p>The conjugative term involves the conception of ''third'', the relative that of second or ''other'', the absolute term simply considers ''an'' object. No fourth class of terms exists involving the conception of ''fourth'', because when that of ''third'' is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. Whether this ''reason'' for the fact that there is no fourth class of terms fundamentally different from the third is satisfactory of not, the fact itself is made perfectly evident by the study of the logic of relatives.</p> |
| − | + | ||
| − | + | <p>(Peirce, CP 3.63).</p> | |
| − | + | |} | |
| − | a, | + | |
| − | + | I am going to experiment with an interlacing commentary on Peirce's 1870 “Logic of Relatives” paper, revisiting some critical transitions from several different angles and calling attention to a variety of puzzles, problems, and potentials that are not so often remarked or tapped. | |
| − | + | ||
| − | + | What strikes me about the initial installment this time around is its use of a certain pattern of argument that I can recognize as invoking a ''closure principle'', and this is a figure of reasoning that Peirce uses in three other places: his discussion of [[continuous predicates]], his definition of [[sign relations]], and in the [[pragmatic maxim]] itself. | |
| + | |||
| + | One might also call attention to the following two statements: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | <p> | + | <p>Now logical terms are of three grand classes.</p> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | |||
| − | |||
| | | | ||
| − | < | + | <p>No fourth class of terms exists involving the conception of ''fourth'', because when that of ''third'' is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship.</p> |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |} | ||
| − | + | ==Selection 2== | |
| − | + | ===Numbers Corresponding to Letters=== | |
| − | {| align="center" | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| | | | ||
| − | < | + | <p>I propose to use the term “universe” to denote that class of individuals ''about'' which alone the whole discourse is understood to run. The universe, therefore, in this sense, as in Mr. De Morgan's, is different on different occasions. In this sense, moreover, discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains.</p> |
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (''men''), the number of “tooth of” would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus <math>[t].\!</math></p> | |
| − | + | <p>(Peirce, CP 3.65).</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | Peirce's remarks at CP 3.65 are so replete with remarkable ideas, some of them so taken for granted in mathematical discourse that they usually escape explicit mention, and others so suggestive of things to come in a future remote from his time of writing, and yet so smoothly introduced in passing that it's all too easy to overlook their consequential significance, that I can do no better here than to highlight these ideas in other words, whose main advantage is to be a little more jarring to the mind's sensibilities. | |
| − | + | :* This mapping of letters to numbers, or logical terms to mathematical quantities, is the very core of what "quantification theory" is all about, and definitely more to the point than the mere "innovation" of using distinctive symbols for the so-called "quantifiers". We will speak of this more later on. | |
| − | + | :* The mapping of logical terms to numerical measures, to express it in current language, would probably be recognizable as some kind of "morphism" or "functor" from a logical domain to a quantitative co-domain. | |
| − | + | :* Notice that Peirce follows the mathematician's usual practice, then and now, of making the status of being an "individual" or a "universal" relative to a discourse in progress. I have come to appreciate more and more of late how radically different this "patchwork" or "piecewise" approach to things is from the way of some philosophers who seem to be content with nothing less than many worlds domination, which means that they are never content and rarely get started toward the solution of any real problem. Just my observation, I hope you understand. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :* It is worth noting that Peirce takes the "plural denotation" of terms for granted, or what's the number of a term for, if it could not vary apart from being one or nil? | |
| − | + | :* I also observe that Peirce takes the individual objects of a particular universe of discourse in a "generative" way, not a "totalizing" way, and thus they afford us with the basis for talking freely about collections, constructions, properties, qualities, subsets, and "higher types", as the phrase is mint. | |
| − | |||
| − | |||
| − | + | ==Selection 3== | |
| − | + | ===The Signs of Inclusion, Equality, Etc.=== | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>I shall follow Boole in taking the sign of equality to signify identity. Thus, if <math>\mathrm{v}\!</math> denotes the Vice-President of the United States, and <math>\mathrm{p}~\!</math> the President of the Senate of the United States,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{v} = \mathrm{p}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>means that every Vice-President of the United States is President of the Senate, and every President of the United States Senate is Vice-President.</p> | ||
| − | {| align="center" | + | <p>The sign “less than” is to be so taken that</p> |
| − | | | + | |- |
| + | | align="center" | <math>\mathrm{f} < \mathrm{m}~\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>means that every Frenchman is a man, but there are men besides Frenchmen. Drobisch has used this sign in the same sense. It will follow from these significations of <math>=\!</math> and <math><\!</math> that the sign <math>-\!\!\!<\!</math> (or <math>\leqq</math>, “as small as”) will mean “is”. Thus,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{f} ~-\!\!\!< \mathrm{m}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>means “every Frenchman is a man”, without saying whether there are any other men or not. So,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{m} ~-\!\!\!< \mathit{l}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>will mean that every mother of anything is a lover of the same thing; although this interpretation in some degree anticipates a convention to be made further on. These significations of <math>=\!</math> and <math><\!</math> plainly conform to the indispensable conditions. Upon the transitive character of these relations the syllogism depends, for by virtue of it, from</p> | ||
| + | |- | ||
| + | | | ||
| + | {| width="100%" | ||
| + | | width="25%" | | ||
| + | | align="center" | <math>\mathrm{f} ~-\!\!\!< \mathrm{m}</math> | ||
| + | | width="25%" | | ||
| + | |- | ||
| + | | <p>and</p> | ||
| + | | align="center" | <math>\mathrm{m} ~-\!\!\!< \mathrm{a}</math> | ||
| + | | | ||
| + | |- | ||
| + | | <p>we can infer that</p> | ||
| + | | align="center" | <math>\mathrm{f} ~-\!\!\!< \mathrm{a}</math> | ||
| + | | | ||
|} | |} | ||
| + | |- | ||
| + | | | ||
| + | <p>that is, from every Frenchman being a man and every man being an animal, that every Frenchman is an animal.</p> | ||
| − | + | <p>But not only do the significations of <math>=\!</math> and <math><\!</math> here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. So, to write <math>5 < 7\!</math> is to say that <math>5\!</math> is part of <math>7\!</math>, just as to write <math>\mathrm{f} < \mathrm{m}~\!</math> is to say that Frenchmen are part of men. Indeed, if <math>\mathrm{f} < \mathrm{m}~\!</math>, then the number of Frenchmen is less than the number of men, and if <math>\mathrm{v} = \mathrm{p}\!</math>, then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.</p> | |
| − | |||
| − | |||
| − | + | <p>(Peirce, CP 3.66).</p> | |
| − | |||
|} | |} | ||
| − | + | The quantifier mapping from terms to their numbers that Peirce signifies by means of the square bracket notation <math>[t]\!</math> has one of its principal uses in providing a basis for the computation of frequencies, probabilities, and all of the other statistical measures that can be constructed from these, and thus in affording what may be called a ''principle of correspondence'' between probability theory and its limiting case in the forms of logic. | |
| − | + | This brings us once again to the relativity of contingency and necessity, as one way of approaching necessity is through the avenue of probability, describing necessity as a probability of 1, but the whole apparatus of probability theory only figures in if it is cast against the backdrop of probability space axioms, the reference class of distributions, and the sample space that we cannot help but to abduce upon the scene of observations. Aye, there's the snake eyes. And with them we can see that there is always an irreducible quantum of facticity to all our necessities. More plainly spoken, it takes a fairly complex conceptual infrastructure just to begin speaking of probabilities, and this setting can only be set up by means of abductive, fallible, hypothetical, and inherently risky mental acts. | |
| − | |||
| − | |||
| − | We have just | + | Pragmatic thinking is the logic of abduction, which is just another way of saying that it addresses the question: “What may be hoped?” We have to face the possibility that it may be just as impossible to speak of “absolute identity” with any hope of making practical philosophical sense as it is to speak of “absolute simultaneity” with any hope of making operational physical sense. |
| − | + | ==Selection 4== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===The Signs for Addition=== | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>The sign of addition is taken by Boole so that</p> | ||
| + | |- | ||
| + | | align="center" | <math>x + y\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>denotes everything denoted by <math>x\!</math>, and, ''besides'', everything denoted by <math>y\!</math>.</p> | ||
| − | + | <p>Thus</p> | |
| + | |- | ||
| + | | align="center" | <math>\mathrm{m} + \mathrm{w}~\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>denotes all men, and, besides, all women.</p> | ||
| − | + | <p>This signification for this sign is needed for connecting the notation of logic with that of the theory of probabilities. But if there is anything which is denoted by both terms of the sum, the latter no longer stands for any logical term on account of its implying that the objects denoted by one term are to be taken ''besides'' the objects denoted by the other.</p> | |
| − | + | <p>For example,</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathrm{f} + \mathrm{u}\!</math> | |
| − | | | ||
|- | |- | ||
| − | | | + | | |
| − | + | <p>means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are ''besides themselves''.</p> | |
| − | + | <p>For this reason alone, in a paper which is published in the Proceedings of the Academy for March 17, 1867, I preferred to take as the regular addition of logic a non-invertible process, such that</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathrm{m} ~+\!\!,~ \mathrm{b}</math> | |
| − | | | ||
|- | |- | ||
| − | | | + | | |
| − | + | <p>stands for all men and black things, without any implication that the black things are to be taken besides the men; and the study of the logic of relatives has supplied me with other weighty reasons for the same determination.</p> | |
| − | + | <p>Since the publication of that paper, I have found that Mr. W. Stanley Jevons, in a tract called ''Pure Logic, or the Logic of Quality'' [1864], had anticipated me in substituting the same operation for Boole's addition, although he rejects Boole's operation entirely and writes the new one with a <math>+\!</math> sign while withholding from it the name of addition.</p> | |
| − | + | <p>It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions. But the notation has other recommendations. The conception of ''taking together'' involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five. Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.</p> | |
| − | + | <p>Addition being taken in this sense, ''nothing'' is to be denoted by ''zero'', for then</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>x ~+\!\!,~ 0 ~=~ x</math> | |
| − | | | + | |- |
| + | | | ||
| + | <p>whatever is denoted by <math>x\!</math>; and this is the definition of ''zero''. This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of ''zero'' and that of nothing, and because we shall thus have</p> | ||
| + | |- | ||
| + | | align="center" | <math>[0] ~=~ 0.</math> | ||
|- | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | < | + | <p>(Peirce, CP 3.67).</p> |
| − | |||
| − | |||
|} | |} | ||
| − | + | A wealth of issues arises here that I hope to take up in depth at a later point, but for the moment I shall be able to mention only the barest sample of them in passing. | |
| − | + | The two papers that precede this one in CP 3 are Peirce's papers of March and September 1867 in the ''Proceedings of the American Academy of Arts and Sciences'', titled “On an Improvement in Boole's Calculus of Logic” and “Upon the Logic of Mathematics”, respectively. Among other things, these two papers provide us with further clues about the motivating considerations that brought Peirce to introduce the “number of a term” function, signified here by square brackets. I have already quoted from the “Logic of Mathematics” paper in a related connection. Here are the links to those excerpts: | |
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | + | <dl style="margin-left:30px;"> | |
| + | <dt>Limited Mark Universes | ||
| + | <dd>[http://web.archive.org/web/20140429004255/http://suo.ieee.org/ontology/msg04349.html (1)] | ||
| + | <dd>[http://web.archive.org/web/20140429004359/http://suo.ieee.org/ontology/msg04350.html (2)] | ||
| + | <dd>[http://web.archive.org/web/20140429004130/http://suo.ieee.org/ontology/msg04351.html (3)] | ||
| + | </dl> | ||
| − | + | In setting up a correspondence between “letters” and “numbers”, Peirce constructs a structure-preserving map from a logical domain to a numerical domain. That he does this deliberately is evidenced by the care that he takes with the conditions under which the chosen aspects of structure are preserved, along with his recognition of the critical fact that zeroes are preserved by the mapping. | |
| − | + | Incidentally, Peirce appears to have an inkling of the problems that would later be caused by using the plus sign for inclusive disjunction, but his advice was overridden by the dialects of applied logic that developed in various communities, retarding the exchange of information among engineering, mathematical, and philosophical specialties all throughout the subsequent century. | |
| − | |||
| − | |||
| − | + | ==Selection 5== | |
| − | + | ===The Signs for Multiplication=== | |
| − | |||
| − | {| align="center" | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| | | | ||
| − | < | + | <p>I shall adopt for the conception of multiplication ''the application of a relation'', in such a way that, for example, <math>\mathit{l}\mathrm{w}~\!</math> shall denote whatever is lover of a woman. This notation is the same as that used by Mr. De Morgan, although he appears not to have had multiplication in his mind.</p> |
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | + | <p><math>\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w})</math> will, then, denote whatever is servant of anything of the class composed of men and women taken together. So that:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w}) ~=~ \mathit{s}\mathrm{m} ~+\!\!,~ \mathit{s}\mathrm{w}.</math> | |
| + | |- | ||
| | | | ||
| − | <math> | + | <p><math>(\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w}</math> will denote whatever is lover or servant to a woman, and:</p> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | align="center" | <math>(\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w} ~=~ \mathit{l}\mathrm{w} ~+\!\!,~ \mathit{s}\mathrm{w}.</math> |
| + | |- | ||
| + | | | ||
| + | <p><math>(\mathit{s}\mathit{l})\mathrm{w}\!</math> will denote whatever stands to a woman in the relation of servant of a lover, and:</p> | ||
| + | |- | ||
| + | | align="center" | <math>(\mathit{s}\mathit{l})\mathrm{w} ~=~ \mathit{s}(\mathit{l}\mathrm{w}).</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>Thus all the absolute conditions of multiplication are satisfied.</p> | ||
| + | |||
| + | <p>The term “identical with ——” is a unity for this multiplication. That is to say, if we denote “identical with ——” by <math>\mathit{1}\!</math> we have:</p> | ||
| + | |- | ||
| + | | align="center" | <math>x \mathit{1} ~=~ x ~ ,</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>whatever relative term <math>x\!</math> may be. For what is a lover of something identical with anything, is the same as a lover of that thing.</p> | ||
| + | |||
| + | <p>(Peirce, CP 3.68).</p> | ||
|} | |} | ||
| − | + | Peirce in 1870 is five years down the road from the Peirce of 1865–1866 who lectured extensively on the role of sign relations in the logic of scientific inquiry, articulating their involvement in the three types of inference, and inventing the concept of “information” to explain what it is that signs convey in the process. By this time, then, the semiotic or sign relational approach to logic is so implicit in his way of working that he does not always take the trouble to point out its distinctive features at each and every turn. So let's take a moment to draw out a few of these characters. | |
| − | + | [[Sign relations]], like any brand of non-trivial [[3-adic relations]], can become overwhelming to think about once the cardinality of the object, sign, and interpretant domains or the complexity of the relation itself ascends beyond the simplest examples. Furthermore, most of the strategies that we would normally use to control the complexity, like neglecting one of the domains, in effect, projecting the 3-adic sign relation onto one of its 2-adic faces, or focusing on a single ordered triple of the form <math>(o, s, i)\!</math> at a time, can result in our receiving a distorted impression of the sign relation's true nature and structure. | |
| − | + | ||
| − | + | I find that it helps me to draw, or at least to imagine drawing, diagrams of the following form, where I can keep tabs on what's an object, what's a sign, and what's an interpretant sign, for a selected set of sign-relational triples. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Here is how I would picture Peirce's example of equivalent terms, <math>\mathrm{v} = \mathrm{p},\!</math> where <math>{}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!</math> denotes the Vice-President of the United States, and <math>{}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!</math> denotes the President of the Senate of the United States. | |
| − | {| align="center" | + | {| align="center" border="0" cellspacing="10" style="text-align:center; width:100%" |
| − | | | + | | [[Image:LOR 1870 Figure 1.jpg]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | height="20px" valign="top" | <math>\text{Figure 1}~\!</math> |
|} | |} | ||
| − | + | Depending on whether we interpret the terms <math>{}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!</math> and <math>{}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!</math> as applying to persons who hold these offices at one particular time or as applying to all those persons who have held these offices over an extended period of history, their denotations may be either singular of plural, respectively. | |
| − | + | As a shortcut technique for indicating general denotations or plural referents, I will use the ''elliptic convention'' that represents these by means of figures like “o o o” or “o … o”, placed at the object ends of sign relational triads. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | For a more complex example, here is how I would picture Peirce's example of an equivalence between terms that comes about by applying one of the distributive laws, for relative multiplication over absolute summation. | |
| − | {| align="center" | + | {| align="center" border="0" cellspacing="10" style="text-align:center; width:100%" |
| − | | | + | | [[Image:LOR 1870 Figure 2.jpg]] |
| − | <math>\ | + | |- |
| − | + | | height="20px" valign="top" | <math>\text{Figure 2}\!</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | ==Selection 6== | |
| − | + | ===The Signs for Multiplication (cont.)=== | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>A conjugative term like ''giver'' naturally requires two correlates, one denoting the thing given, the other the recipient of the gift.</p> | ||
| − | + | <p>We must be able to distinguish, in our notation, the giver of <math>\mathrm{A}\!</math> to <math>\mathrm{B}\!</math> from the giver to <math>\mathrm{A}\!</math> of <math>\mathrm{B}\!</math>, and, therefore, I suppose the signification of the letter equivalent to such a relative to distinguish the correlates as first, second, third, etc., so that “giver of —— to ——” and “giver to —— of ——” will be expressed by different letters.</p> | |
| − | + | <p>Let <math>\mathfrak{g}</math> denote the latter of these conjugative terms. Then, the correlates or multiplicands of this multiplier cannot all stand directly after it, as is usual in multiplication, but may be ranged after it in regular order, so that:</p> | |
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}\mathit{x}\mathit{y}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>will denote a giver to <math>\mathit{x}\!</math> of <math>\mathit{y}\!</math>.</p> | ||
| − | { | + | <p>But according to the notation, <math>\mathit{x}\!</math> here multiplies <math>\mathit{y}\!</math>, so that if we put for <math>\mathit{x}\!</math> owner (<math>\mathit{o}\!</math>), and for <math>\mathit{y}\!</math> horse (<math>\mathrm{h}\!</math>),</p> |
| − | |||
|- | |- | ||
| − | | | + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> |
|- | |- | ||
| − | | | + | | |
| + | <p>appears to denote the giver of a horse to an owner of a horse. But let the individual horses be <math>\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}</math>, etc.</p> | ||
| + | |||
| + | <p>Then:</p> | ||
|- | |- | ||
| − | | | + | | align="center" | <math>\mathrm{h} ~=~ \mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}</math> |
|- | |- | ||
| − | | | + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h} ~=~ \mathfrak{g}\mathit{o}(\mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}) ~=~ \mathfrak{g}\mathit{o}\mathrm{H} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}</math> |
| − | |} | ||
| − | |||
| − | |||
| − | |||
| − | { | ||
| − | |||
|- | |- | ||
| − | | | + | | |
| − | |} | + | <p>Now this last member must be interpreted as a giver of a horse to the owner of ''that'' horse, and this, therefore must be the interpretation of <math>\mathfrak{g}\mathit{o}\mathrm{h}</math>. This is always very important. ''A term multiplied by two relatives shows that the same individual is in the two relations.''</p> |
| + | |||
| + | <p>If we attempt to express the giver of a horse to a lover of a woman, and for that purpose write:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}\mathit{l}\mathrm{w}\mathrm{h}</math>, | ||
| + | |- | ||
| + | | | ||
| + | <p>we have written giver of a woman to a lover of her, and if we add brackets, thus,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}(\mathit{l}\mathrm{w})\mathrm{h}</math>, | ||
| + | |- | ||
| + | | | ||
| + | <p>we abandon the associative principle of multiplication.</p> | ||
| − | + | <p>A little reflection will show that the associative principle must in some form or other be abandoned at this point. But while this principle is sometimes falsified, it oftener holds, and a notation must be adopted which will show of itself when it holds. We already see that we cannot express multiplication by writing the multiplicand directly after the multiplier; let us then affix subjacent numbers after letters to show where their correlates are to be found. The first number shall denote how many factors must be counted from left to right to reach the first correlate, the second how many ''more'' must be counted to reach the second, and so on.</p> | |
| − | + | <p>Then, the giver of a horse to a lover of a woman may be written:</p> | |
| − | | | + | |- |
| − | + | | align="center" | <math>\mathfrak{g}_{12} \mathit{l}_1 \mathrm{w} \mathrm{h} ~=~ \mathfrak{g}_{11} \mathit{l}_2 \mathrm{h} \mathrm{w} ~=~ \mathfrak{g}_{2(-1)} \mathrm{h} \mathit{l}_1 \mathrm{w}</math>. | |
| + | |- | ||
| + | | | ||
| + | <p>Of course a negative number indicates that the former correlate follows the latter by the corresponding positive number.</p> | ||
| − | + | <p>A subjacent ''zero'' makes the term itself the correlate.</p> | |
| − | {| align="center" | + | <p>Thus,</p> |
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_0\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>denotes the lover of ''that'' lover or the lover of himself, just as <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> denotes that the horse is given to the owner of itself, for to make a term doubly a correlate is, by the distributive principle, to make each individual doubly a correlate, so that:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_0 ~=~ \mathit{L}_0 ~+\!\!,~ \mathit{L}_0^{\prime} ~+\!\!,~ \mathit{L}_0^{\prime\prime} ~+\!\!,~ \text{etc.}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>A subjacent sign of infinity may indicate that the correlate is indeterminate, so that:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_\infty</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>will denote a lover of something. We shall have some confirmation of this presently.</p> | ||
| + | |||
| + | <p>If the last subjacent number is a ''one'' it may be omitted. Thus we shall have:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_1 ~=~ \mathit{l}</math>, | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}_{11} ~=~ \mathfrak{g}_1 ~=~ \mathfrak{g}</math>. | ||
| + | |- | ||
| | | | ||
| − | <math>\ | + | <p>This enables us to retain our former expressions <math>\mathit{l}\mathrm{w}~\!</math>, <math>\mathfrak{g}\mathit{o}\mathrm{h}</math>, etc.</p> |
| − | + | ||
| − | + | <p>(Peirce, CP 3.69–70).</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | ===Comment : Sets as Logical Sums=== | |
| + | |||
| + | Peirce's way of representing sets as logical sums may seem archaic, but it is quite often used, and is actually the tool of choice in many branches of algebra, combinatorics, computing, and statistics to this very day. | ||
| − | + | Peirce's application to logic is fairly novel, and the degree of his elaboration of the logic of relative terms is certainly original with him, but this particular genre of representation, commonly going under the handle of ''generating functions'', goes way back, well before anyone thought to stick a flag in set theory as a separate territory or to try to fence off our native possessions of it with expressly decreed axioms. And back in the days when a computer was just a person who computed, before we had the sorts of ''electronic register machines'' that we take so much for granted today, mathematicians were constantly using generating functions as a rough and ready type of addressable memory to sort, store, and keep track of their accounts of a wide variety of formal objects of thought. | |
| − | + | Let us look at a few simple examples of generating functions, much as I encountered them during my own first adventures in the Fair Land Of Combinatoria. | |
| − | {| align="center" | + | Suppose that we are given a set of three elements, say, <math>\{ a, b, c \},\!</math> and we are asked to find all the ways of choosing a subset from this collection. |
| − | | | + | |
| − | + | We can represent this problem setup as the problem of computing the following product: | |
| − | + | ||
| − | <math> | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | <math>(1 + a)(1 + b)(1 + c).\!</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | The factor <math>(1 + a)\!</math> represents the option that we have, in choosing a subset of <math>\{ a, b, c \},\!</math> to leave the element <math>a\!</math> out (signified by the <math>1\!</math>), or else to include it (signified by the <math>a\!</math>), and likewise for the other elements <math>b\!</math> and <math>c\!</math> in their turns. | |
| − | + | Probably on account of all those years I flippered away playing the oldtime pinball machines, I tend to imagine a product like this being displayed in a vertical array: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | |||
| − | {| align="center" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{matrix} |
| − | + | (1 ~+~ a) | |
| − | + | \\ | |
| − | + | (1 ~+~ b) | |
| − | + | \\ | |
| − | + | (1 ~+~ c) | |
| − | \ | + | \end{matrix}</math> |
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \end{ | ||
|} | |} | ||
| − | + | I picture this as a playboard with six bumpers, the ball chuting down the board in such a career that it strikes exactly one of the two bumpers on each and every one of the three levels. | |
| − | + | So a trajectory of the ball where it hits the <math>a\!</math> bumper on the 1st level, hits the <math>1\!</math> bumper on the 2nd level, hits the <math>c\!</math> bumper on the 3rd level, and then exits the board, represents a single term in the desired product and corresponds to the subset <math>\{ a, c \}.\!</math> | |
| − | |||
| − | <math>\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Multiplying out the product <math>(1 + a)(1 + b)(1 + c),\!</math> one obtains: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | |||
| − | {| align="center" | ||
| | | | ||
| − | <math>\begin{array}{ | + | <math>\begin{array}{*{15}{c}} |
| − | + | 1 & + & a & + & b & + & c & + & ab & + & ac & + & bc & + & abc. | |
| − | + | \end{array}</math> | |
| − | |||
| − | |||
| − | |||
| − | \end{array} | ||
|} | |} | ||
| − | + | And this informs us that the subsets of choice are: | |
| − | {| align="center" | + | {| align="center" cellspacing="6" width="90%" |
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | \ | + | \varnothing, & \{ a \}, & \{ b \}, & \{ c \}, & \{ a, b \}, & \{ a, c \}, & \{ b, c \}, & \{ a, b, c \}. |
| − | & | + | \end{matrix}</math> |
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | \ | ||
| − | \end{matrix} | ||
|} | |} | ||
| − | + | ==Selection 7== | |
| − | {| align="center" | + | ===The Signs for Multiplication (cont.)=== |
| − | | | + | |
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| + | | | ||
| + | <p>The associative principle does not hold in this counting of factors. Because it does not hold, these subjacent numbers are frequently inconvenient in practice, and I therefore use also another mode of showing where the correlate of a term is to be found. This is by means of the marks of reference, <math>\dagger ~ \ddagger ~ \parallel ~ \S ~ \P</math>, which are placed subjacent to the relative term and before and above the correlate. Thus, giver of a horse to a lover of a woman may be written:</p> | ||
|- | |- | ||
| − | | | + | | align="center" | <math>\mathfrak{g}_{\dagger\ddagger} \, ^\dagger\mathit{l}_\parallel \, ^\parallel\mathrm{w} \, ^\ddagger\mathrm{h}</math> |
|- | |- | ||
| − | | | + | | |
| − | + | <p>The asterisk I use exclusively to refer to the last correlate of the last relative of the algebraic term.</p> | |
| − | + | ||
| − | + | <p>Now, considering the order of multiplication to be: — a term, a correlate of it, a correlate of that correlate, etc. — there is no violation of the associative principle. The only violations of it in this mode of notation are that in thus passing from relative to correlate, we skip about among the factors in an irregular manner, and that we cannot substitute in such an expression as <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> a single letter for <math>\mathit{o}\mathrm{h}.\!</math></p> | |
| − | + | ||
| + | <p>I would suggest that such a notation may be found useful in treating other cases of non-associative multiplication. By comparing this with what was said above [in CP 3.55] concerning functional multiplication, it appears that multiplication by a conjugative term is functional, and that the letter denoting such a term is a symbol of operation. I am therefore using two alphabets, the Greek and Kennerly, where only one was necessary. But it is convenient to use both.</p> | ||
| + | |||
| + | <p>(Peirce, CP 3.71–72).</p> | ||
|} | |} | ||
| − | + | ===Comment : Proto-Graphical Syntax=== | |
| − | + | It is clear from our last excerpt that Peirce is already on the verge of a graphical syntax for the logic of relatives. Indeed, it seems likely that he had already reached this point in his own thinking. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | For instance, it seems quite impossible to read his last variation on the theme of a “giver of a horse to a lover of a woman” without drawing lines of identity to connect up the corresponding marks of reference, like this: | |
| − | {| align="center" cellpadding="10 | + | {| align="center" cellpadding="10" |
| − | | [[Image: | + | | [[Image:LOR 1870 Figure 3.jpg]] || (3) |
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | ==Selection 8== | |
| − | == | + | ===The Signs for Multiplication (cont.)=== |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>Thus far, we have considered the multiplication of relative terms only. Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives.</p> | ||
| − | + | <p>Now the absolute term “man” is really exactly equivalent to the relative term “man that is ——”, and so with any other. I shall write a comma after any absolute term to show that it is so regarded as a relative term.</p> | |
| − | < | + | <p>Then “man that is black” will be written:</p> |
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},\!\mathrm{b}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one.</p> | ||
| − | + | <p>Then:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathit{l},\!\mathit{s}\mathrm{w}</math> | |
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| | | | ||
| − | <math>\ | + | <p>will denote a lover of a woman that is a servant of that woman.</p> |
| − | + | ||
| − | \\ | + | <p>The comma here after <math>\mathit{l}\!</math> should not be considered as altering at all the meaning of <math>\mathit{l}\!</math>, but as only a subjacent sign, serving to alter the arrangement of the correlates.</p> |
| − | + | ||
| − | \ | + | <p>In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates.</p> |
| − | + | ||
| − | + | <p>So:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathrm{m},\!,\!\mathrm{b},\!\mathrm{r}</math> | |
| − | + | |- | |
| − | \\ | ||
| − | |||
| − | \\ | ||
| − | |||
| − | \\ | ||
| − | |||
| − | |||
| | | | ||
| − | < | + | <p>interpreted like</p> |
| − | + | |- | |
| − | \ | + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> |
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | < | + | <p>means a man that is a rich individual and is a black that is that rich individual.</p> |
| − | + | ||
| − | + | <p>But this has no other meaning than:</p> | |
| − | + | |- | |
| − | \\ | + | | align="center" | <math>\mathrm{m},\!\mathrm{b},\!\mathrm{r}</math> |
| − | + | |- | |
| − | \\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | <math>\ | + | <p>or a man that is a black that is rich.</p> |
| − | ( | + | |
| − | + | <p>Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number.</p> | |
| − | (p | + | |
| − | + | <p>If, therefore, <math>\mathit{l},\!,\!\mathit{s}\mathrm{w}</math> is not the same as <math>\mathit{l},\!\mathit{s}\mathrm{w}</math> (as it plainly is not, because the latter means a lover and servant of a woman, and the former a lover of and servant of and same as a woman), this is simply because the writing of the comma alters the arrangement of the correlates.</p> | |
| − | + | ||
| − | + | <p>And if we are to suppose that absolute terms are multipliers at all (as mathematical generality demands that we should}, we must regard every term as being a relative requiring an infinite number of correlates to its virtual infinite series “that is —— and is —— and is —— etc.”</p> | |
| − | + | ||
| − | \\ | + | <p>Now a relative formed by a comma of course receives its subjacent numbers like any relative, but the question is, What are to be the implied subjacent numbers for these implied correlates?</p> |
| − | ~ | + | |
| − | \\ | + | <p>Any term may be regarded as having an infinite number of factors, those at the end being ''ones'', thus:</p> |
| − | + | |- | |
| − | \\ | + | | align="center" | <math>\mathit{l},\!\mathit{s}\mathrm{w} ~=~ \mathit{l},\!\mathit{s}\mathit{w},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1}, ~\text{etc.}</math> |
| − | + | |- | |
| − | \\ | ||
| − | |||
| − | \ | ||
| | | | ||
| − | < | + | <p>A subjacent number may therefore be as great as we please.</p> |
| − | + | ||
| − | + | <p>But all these ''ones'' denote the same identical individual denoted by <math>\mathrm{w}\!</math>; what then can be the subjacent numbers to be applied to <math>\mathit{s}\!</math>, for instance, on account of its infinite “''that is''”'s? What numbers can separate it from being identical with <math>\mathrm{w}\!</math>? There are only two. The first is ''zero'', which plainly neutralizes a comma completely, since</p> | |
| − | + | |- | |
| − | \\ | + | | align="center" | <math>\mathit{s},_0\!\mathrm{w} ~=~ \mathit{s}\mathrm{w}</math> |
| − | + | |- | |
| − | \\ | ||
| − | |||
| − | \ | ||
| − | p | ||
| − | |||
| − | \ | ||
| − | \\ | ||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| | | | ||
| − | <math>\ | + | <p>and the other is infinity; for as <math>1^\infty</math> is indeterminate in ordinary algbra, so it will be shown hereafter to be here, so that to remove the correlate by the product of an infinite series of ''ones'' is to leave it indeterminate.</p> |
| − | + | ||
| − | + | <p>Accordingly,</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathrm{m},_\infty</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | ||
|- | |- | ||
| | | | ||
| − | < | + | <p>should be regarded as expressing ''some'' man.</p> |
| − | + | ||
| − | + | <p>Any term, then, is properly to be regarded as having an infinite number of commas, all or some of which are neutralized by zeros.</p> | |
| − | + | ||
| − | + | <p>“Something” may then be expressed by:</p> | |
| − | + | |- | |
| − | \ | + | | align="center" | <math>\mathit{1}_\infty\!</math> |
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| | | | ||
| − | <math>\ | + | <p>I shall for brevity frequently express this by an antique figure one <math>(\mathfrak{1}).</math></p> |
| − | + | ||
| − | + | <p>“Anything” by:</p> | |
| − | + | |- | |
| − | \ | + | | align="center" | <math>\mathit{1}_0\!</math> |
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | <math> | + | <p>I shall often also write a straight <math>1\!</math> for ''anything''.</p> |
| − | 1 | + | |
| − | \ | + | <p>(Peirce, CP 3.73).</p> |
| − | + | |} | |
| − | + | ||
| − | + | ==Commentary Work Area== | |
| − | + | ||
| − | + | ===Commentary Note 12.2=== | |
| − | + | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | < | + | <pre> |
| − | + | a b c d e f g h i | |
| − | + | o o o o o o o o o X | |
| − | + | | | : | : | | |
| − | + | | | 0 1 0 1 W, | |
| − | + | | | : | : | | |
| − | \ | + | o o o o + - + + o X |
| − | + | \ | / : : | | | |
| − | + | \ | / 0 0 1 1 L | |
| − | + | \|/ : : | | | |
| − | + | o o o o o o o o o X | |
| − | + | a b c d e f g h i | |
| − | + | </pre> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <pre> | ||
| + | a b c d e f g h i | ||
| + | o o o o o o o o o X | ||
| + | / \ : | : | | ||
| + | / \ 0 1 0 1 L | ||
| + | / \ : | : | | ||
| + | o o o o + - + + o X | ||
| + | \ | / : : | | | ||
| + | \ | / 0 0 1 1 S | ||
| + | \|/ : : | | | ||
| + | o o o o o o o o o X | ||
| + | a b c d e f g h i | ||
| + | </pre> | ||
| + | |} | ||
| − | + | ===Commentary Note 12.3=== | |
| − | + | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | < | + | <pre> |
| − | + | a b c d e f g h i | |
| − | \\ | + | o o o o o o o o o X |
| − | + | | | | |
| − | \\ | + | | | W, |
| − | + | | | | |
| − | \\ | + | o o o o o o o o o X |
| − | + | \ \ / / \ | / \ \ / / | |
| − | + | \ / / \ | / \ \ / L | |
| + | \ / \ / \|/ \ / \ / | ||
| + | o o o o o o o o o X | ||
| + | a b c d e f g h i | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | ===Commentary Note 12.4=== | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{*{15}{c}} |
| − | + | X & = & \{ & a, & b, & c, & d, & e, & f, & g, & h, & i\ & \} | |
| − | \\[ | + | \\[6pt] |
| − | + | W & = & \{ & d, & f\ & \} | |
| − | \\[ | + | \\[6pt] |
| − | + | L & = & \{ & b\!:\!a, & b\!:\!c, & c\!:\!b, & c\!:\!d, & e\!:\!d, & e\!:\!e, & e\!:\!f, & g\!:\!f, & g\!:\!h, & h\!:\!g, & h\!:\!i & \} | |
| − | \\[ | + | \\[6pt] |
| − | + | S & = & \{ & b\!:\!a, & b\!:\!c, & d\!:\!c, & d\!:\!d, & d\!:\!e, & f\!:\!e, & f\!:\!f, & f\!:\!g, & h\!:\!g, & h\!:\!i\ & \} | |
| − | \end{ | + | \end{array}</math> |
| + | |} | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | < | + | <pre> |
| − | + | a b c d e f g h i | |
| − | \\ | + | o o o o o o o o o X |
| − | + | | | | |
| − | \\ | + | | | W, |
| − | + | | | | |
| − | \\ | + | o o o o o o o o o X |
| − | + | \ \ / / \ | / \ \ / / | |
| − | \ | + | \ / / \ | / \ \ / L |
| + | \ / \ / \|/ \ / \ / | ||
| + | o o o o o o o o o X | ||
| + | \ / \ | / \ | / \ / | ||
| + | \ / \ | / \ | / \ / S | ||
| + | \ / \|/ \|/ \ / | ||
| + | o o o o o o o o o X | ||
| + | a b c d e f g h i | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | < | + | <pre> |
| − | ( | + | a b c d e f g h i |
| − | \\ | + | o o o o o o o o o X |
| − | + | | | |
| − | \\ | + | | (LW), |
| − | + | | | |
| − | \\ | + | o o o o o o o o o X |
| − | + | \ / \ | / \ | / \ / | |
| − | + | \ / \ | / \ | / \ / S | |
| + | \ / \|/ \|/ \ / | ||
| + | o o o o o o o o o X | ||
| + | a b c d e f g h i | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | < | + | <pre> |
| − | + | a b c d e f g h i | |
| − | + | o o o o o o o o o X | |
| − | + | | | | |
| − | + | | | (S^(LW)), | |
| − | + | | | | |
| − | + | o o o o o o o o o X | |
| − | + | a b c d e f g h i | |
| − | + | </pre> | |
| + | |} | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | < | + | <pre> |
| − | \ | + | a b c d e f g h i |
| − | \\ | + | o o o o o o o o o X |
| − | \ | + | \ \ / / \ | / \ \ / / |
| − | \\ | + | \ / / \ | / \ \ / L |
| − | + | \ / \ / \|/ \ / \ / | |
| − | \\ | + | o o o o o o o o o X |
| − | + | \ / \ | / \ | / \ / | |
| − | \ | + | \ / \ | / \ | / \ / S |
| − | + | \ / \|/ \|/ \ / | |
| − | + | o o o o o o o o o X | |
| − | < | + | a b c d e f g h i |
| − | + | </pre> | |
| − | + | |} | |
| − | + | ||
| − | + | ===Commentary Note 12.5=== | |
| − | | | + | |
| − | <math>\ | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="80" | | |
| − | \\ | + | <math> |
| − | + | (\mathsf{L} \mathsf{W})_x ~=~ | |
| − | \ | + | \sum_{p \in X} \mathsf{L}_{xp} \mathsf{W}_p |
| − | | | + | </math> |
| − | <math>\ | + | |} |
| − | + | ||
| − | \\ | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="80" | | |
| − | \ | + | <math> |
| − | | | + | (\mathsf{L} \mathsf{W})_q ~=~ |
| − | <math>\ | + | \sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p |
| − | + | </math> | |
| − | \\ | + | |} |
| − | + | ||
| − | \ | + | {| align="center" cellspacing="6" width="90%" |
| − | | | + | | height="80" | |
| − | <math>\ | + | <math>(\mathsf{L}^\mathsf{W})_x ~=~ |
| − | \ | + | \prod_{p \in X} \mathsf{L}_{xp}^{\mathsf{W}_p} |
| − | \\ | + | </math> |
| − | + | |} | |
| − | \ | + | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | <math>\ | + | | height="80" | |
| − | \ | + | <math> |
| − | \\ | + | (\mathsf{S}^\mathsf{L})_{xy} ~=~ |
| − | + | \prod_{p \in X} \mathsf{S}_{xp}^{\mathsf{L}_{py}} | |
| − | \ | + | </math> |
| − | | | + | |} |
| − | | | + | |
| − | <math>\ | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="80" | | |
| − | \\ | + | <math> |
| − | + | (\mathsf{S}^\mathsf{L})_{xp} ~=~ | |
| − | \ | + | \prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}} |
| − | | | + | </math> |
| − | <math>\ | + | |} |
| − | + | ||
| − | \\ | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="80" | | |
| − | \ | + | <math> |
| − | + | ((\mathsf{S}^\mathsf{L})^\mathsf{W})_x ~=~ | |
| − | + | (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x | |
| − | + | </math> | |
| − | \\ | + | |} |
| − | + | ||
| − | \ | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="80" | | |
| − | + | <math> | |
| − | ~ | + | ((\mathsf{S}^\mathsf{L})^\mathsf{W})_x ~=~ |
| − | \\ | + | \prod_{p \in X} (\mathsf{S}^\mathsf{L})_{xp}^{\mathsf{W}_p} ~=~ |
| − | + | \prod_{p \in X} (\prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}})^{\mathsf{W}_p} ~=~ | |
| − | \ | + | \prod_{p \in X} \prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}\mathsf{W}_p} |
| − | | | + | </math> |
| − | <math>\ | + | |} |
| − | + | ||
| − | \\ | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="80" | | |
| − | \ | + | <math> |
| − | + | (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x ~=~ | |
| − | + | \prod_{q \in X} \mathsf{S}_{xq}^{(\mathsf{L}\mathsf{W})_q} ~=~ | |
| − | + | \prod_{q \in X} \mathsf{S}_{xq}^{\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p} ~=~ | |
| − | \\ | + | \prod_{q \in X} \prod_{p \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp} \mathsf{W}_p} |
| − | p | + | </math> |
| − | \ | + | |} |
| − | + | ||
| − | + | ===Commentary Note 12.6=== | |
| − | + | ||
| − | + | Need a comment about the meaning of the sum <math>\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p\!</math> in the following equation: | |
| − | \\ | + | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | \ | ||
| − | | | ||
| − | <math>\ | ||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| | | | ||
| − | <math>\ | + | <math> |
| − | + | (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x ~=~ | |
| − | \\ | + | \prod_{q \in X} \mathsf{S}_{xq}^{(\mathsf{L}\mathsf{W})_q} ~=~ |
| − | + | \prod_{q \in X} \mathsf{S}_{xq}^{\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p} ~=~ | |
| − | \ | + | \prod_{q \in X} \prod_{p \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp} \mathsf{W}_p}\! |
| − | | | + | </math> |
| − | <math>\ | + | |} |
| − | ( | + | |
| − | \\ | + | {| align="center" cellspacing="6" width="90%" |
| − | ~ | + | | <math>(\mathsf{L}\mathsf{W})_q ~=~ \sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p\!</math> |
| − | \ | + | |} |
| − | | | + | |
| − | <math>\ | + | {| align="center" cellspacing="6" width="90%" |
| − | \ | + | | <math>(\mathsf{L}\mathsf{W})_x ~=~ \sum_{p \in X} \mathsf{L}_{xp} \mathsf{W}_p\!</math> |
| − | \\ | + | |} |
| − | + | ||
| − | \ | + | {| align="center" cellspacing="6" width="90%" |
| + | | <math>\mathrm{w} ~=~ \sum_{x \in X} \mathsf{W}_x x \quad ?\!</math> | ||
| + | |} | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| + | | <math>\mathrm{w} ~=~ \sum_\mathbf{1} \mathrm{w}_\mathrm{X} \mathrm{X} \quad ?\!</math> | ||
| + | |} | ||
| + | |||
| + | ===Commentary Note 12.7=== | ||
| + | |||
| + | * Problem about the relation of logical involution to the function space <math>Y^X = \{ f : X \to Y \}.</math> | ||
| + | ** Notice that a function <math>f : X \to Y</math> is a "<math>Y\!</math>-evaluator of every <math>X,\!</math> or a "giver of a <math>Y\!</math>-value to every element of <math>X\!</math>". | ||
| + | |||
| + | ===Commentary on Selection 12 : Old Notes=== | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | <math>\ | + | <p>Then</p> |
| − | \ | + | |- |
| − | + | | align="center" | <math>(\mathit{s}^\mathit{l})^\mathrm{w}\!</math> | |
| − | |||
| − | \ | ||
|- | |- | ||
| | | | ||
| − | < | + | <p>will denote whatever stands to every woman in the relation of servant of every lover of hers;</p> |
| − | + | ||
| − | + | <p>and</p> | |
| − | + | |- | |
| − | \ | + | | align="center" | <math>\mathit{s}^{(\mathit{l}\mathrm{w})}\!</math> |
| − | + | |- | |
| − | |||
| − | |||
| − | \ | ||
| | | | ||
| − | <math>\ | + | <p>will denote whatever is a servant of everything that is lover of a woman.</p> |
| − | + | ||
| − | + | <p>So that</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>(\mathit{s}^\mathit{l})^\mathrm{w} ~=~ \mathit{s}^{(\mathit{l}\mathrm{w})}.</math> | |
| − | + | |- | |
| − | |||
| − | |||
| − | \ | ||
| | | | ||
| − | < | + | <p>(Peirce, CP 3.77).</p> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | Then we have the following results: | |
| − | + | {| align="left" cellspacing="6" width="100%" | |
| − | + | |- style="height:60px" | |
| − | + | | width="5%" | | |
| − | + | | width="10%" | <math>\mathit{s}^{(\mathit{l}\mathrm{w})}\!</math> | |
| − | + | | width="5%" | <math>=\!</math> | |
| − | + | | width="20%" | <math>\bigcap_{x \in LW} \operatorname{proj}_1 (S \star x)</math> | |
| − | {| align=" | + | | width="60%" | |
| − | + | |- style="height:60px" | |
| − | |- style=" | + | | |
| − | | width=" | + | | <math>(\mathit{s}^\mathit{l})^\mathrm{w}\!</math> |
| − | | width=" | + | | <math>=\!</math> |
| − | + | | <math>\bigcap_{x \in W} \operatorname{proj}_1 (S^L \star x) \quad ???</math> | |
| − | + | | | |
| − | + | |} | |
| − | | width=" | + | |
| − | + | But what is <math>S^L \quad ???</math> | |
| − | + | ||
| − | | width=" | + | Suppose we try this: |
| − | + | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | | | + | | <math>S^L ~=~ \bigcap_{x \in \operatorname{proj}_1 L} \operatorname{proj}_1 (S \star x)\!</math> |
| − | + | |} | |
| − | + | ||
| − | | | + | No, it looks like I need to think about this some more … |
| − | | <math> | + | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | | <math> | ||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| | | | ||
| − | < | + | <pre> |
| − | + | a b c d e f g h i | |
| − | \\ | + | o o o o o o o o o X |
| − | + | / \ : | : | | |
| − | \ | + | / \ 0 1 0 1 L |
| − | + | / \ : | : | | |
| − | + | o o o o + - + + o X | |
| − | + | \ | / : : | | | |
| − | + | \ | / 0 0 1 1 S | |
| − | + | \|/ : : | | | |
| − | <math>\ | + | o o o o o o o o o X |
| − | + | a b c d e f g h i | |
| − | \\ | + | </pre> |
| − | + | |} | |
| − | \ | + | |
| − | + | It looks like there is a "servant of every lover of" link between <math>i\!</math> and <math>j\!</math> if and only if <math>i \cdot S ~\supseteq~ L \cdot j.</math> But the vacuous inclusions will make this non-intuitive. | |
| − | + | ||
| − | + | Recall the analogy between involution and implication: | |
| − | + | ||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math> |
| − | + | \begin{bmatrix} | |
| − | \\ | + | 0^0 & = & 1 |
| − | + | \\ | |
| − | \\ | + | 0^1 & = & 0 |
| − | + | \\ | |
| − | \\ | + | 1^0 & = & 1 |
| − | + | \\ | |
| − | \end{ | + | 1^1 & = & 1 |
| − | + | \end{bmatrix} | |
| − | + | \qquad\qquad\qquad | |
| − | + | \begin{bmatrix} | |
| − | \\ | + | 0\!\Leftarrow\!0 & = & 1 |
| − | + | \\ | |
| − | \\ | + | 0\!\Leftarrow\!1 & = & 0 |
| − | + | \\ | |
| − | \\ | + | 1\!\Leftarrow\!0 & = & 1 |
| − | + | \\ | |
| − | \ | + | 1\!\Leftarrow\!1 & = & 1 |
| − | + | \end{bmatrix} | |
| − | + | </math> | |
| − | + | |} | |
| − | \\ | + | |
| − | + | So it begins to look like this: | |
| − | \\ | + | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | \\ | + | | <math>(\mathsf{S}^\mathsf{L})_{ab} ~=~ \prod_{x \in X} \mathsf{S}_{ax}^{\mathsf{L}_{xb}}\!</math> |
| − | + | |} | |
| − | \end{ | + | |
| − | | | + | In other words, <math>(\mathsf{S}^\mathsf{L})_{ab} = 0\!</math> if and only if there exists an <math>x \in X\!</math> such that <math>\mathsf{S}_{ax} = 0\!</math> and <math>\mathsf{L}_{xb} = 1.\!</math> |
| − | <math>\ | + | |
| − | + | ===Commentary on Selection 12 : Older Notes=== | |
| − | \ | + | |
| − | + | The logic of terms is something of a lost art these days, when the current thinking in logic tends to treat the complete proposition as the quantum of discourse, ''ne plus infra''. With absolute terms, or monadic relatives, and the simpler operations on dyadic relatives, the necessary translations between propositions and terms are obvious enough, but now that we've reached the threshold of higher adic relatives and operations as complex as exponentiation, it is useful to stop and consider the links between these two languages. | |
| − | \\ | + | |
| − | + | The term ''exponentiation'' is more generally used in mathematics for operations that involve taking a base to a power, and is slightly preferable to ''involution'' since the latter is used for different concepts in different contexts. Operations analogous to taking powers are widespread throughout mathematics and Peirce frequently makes use of them in a number of important applications, for example, in his theory of information. But that's another story. | |
| − | \\ | + | |
| − | + | The ''function space'' <math>Y^X,\!</math> where <math>X\!</math> and <math>Y\!</math> are sets, is the set of all functions from <math>X\!</math> to <math>Y.\!</math> An alternative notation for <math>Y^X\!</math> is <math>(X \to Y).\!</math> Thus we have the following equivalents: | |
| − | + | ||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | <math>\begin{matrix}Y^X & = & (X \to Y) & = & \{ f : X \to Y \}\end{matrix}\!</math> | |
| − | <math>\ | + | |} |
| − | + | ||
| − | + | If <math>X\!</math> and <math>Y\!</math> have cardinalities <math>|X|\!</math> and <math>|Y|,\!</math> respectively, then the function space <math>Y^X\!</math> has a cardinality given by the following equation: | |
| − | + | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>\begin{matrix}|Y^X| & = & |Y|^{|X|}\end{matrix}\!</math> | |
| − | <math>\ | + | |} |
| − | + | ||
| − | + | In the special case where <math>Y = \mathbb{B} = \{ 0, 1 \},\!</math> the function space <math>\mathbb{B}^X\!</math> is the set of functions <math>\{ f : X \to \mathbb{B} \}.\!</math> If the elements <math>0, 1 \in \mathbb{B}\!</math> are interpreted as the logical values <math>\mathrm{false}, \mathrm{true},\!</math> respectively, then a function of the type <math>X \to \mathbb{B}\!</math> may be interpreted as a ''proposition'' about the elements in <math>X.\!</math> | |
| − | + | ||
| − | + | ===Really Old Commentary Notes=== | |
| − | + | ||
| − | <math>\ | + | <pre> |
| − | + | Up to this point in the discussion, we have observed that | |
| − | + | the "number of" map 'v' : S -> R such that 'v's = [s] has | |
| − | + | the following morphic properties: | |
| − | + | ||
| − | + | 0. [0] = 0 | |
| − | <math>\ | + | |
| − | + | 1. 'v' | |
| − | + | ||
| − | + | 2. x -< y => [x] =< [y] | |
| − | + | ||
| − | + | 3. [x +, y] =< [x] + [y] | |
| − | + | ||
| − | + | contingent: | |
| − | + | ||
| − | + | 4. [xy] = [x][y] | |
| − | \ | + | |
| − | + | view relation P c X x Y x Z as related to three functions: | |
| − | <math>\ | + | |
| − | + | `p_1` c | |
| − | \ | + | `p_3` c X x Y x Pow(Z) |
| − | + | ||
| − | + | ||
| − | + | f(x) | |
| − | + | ||
| − | <math> | + | f(x+y) = f(x) + f(y) |
| − | + | ||
| − | + | f(p(x, y)) = q(f(x), f(y)) | |
| − | + | ||
| − | + | P(x, y, z) | |
| − | + | ||
| − | <math> | + | (f^-1)(y) |
| − | + | ||
| − | \ | + | f(z(x, y)) = z'(f(x), f(y)) |
| − | + | ||
| − | + | Definition. f(x:y:z) = (fx:fy:fz). | |
| − | | | + | |
| − | <math>\begin{matrix} | + | f(x:y:z) = (fx:fy: |
| − | + | ||
| − | \\ | + | x:y:z in R => fx:fy:fz in fR |
| − | + | ||
| − | \end{matrix}\!</math> | + | R(x, y, z) => (fR)(fx, fy, fz) |
| − | | | + | |
| − | <math>\ | + | (L, x, y, z) => (fL, fx, fy, fz) |
| − | + | ||
| − | \ | + | (x, y, z, L) => (xf, yf, zf, Lf) |
| − | + | ||
| − | + | (x, y, z, b) => (xf, yf, zf, bf) | |
| − | |||
| − | <math> | ||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | | | ||
| − | <math>\begin{matrix} | ||
| − | |||
| − | |||
| − | |||
| − | \end{matrix}\!</math> | ||
| − | | | ||
| − | |||
| − | <math>\ | ||
| − | |||
| − | \ | ||
| − | |||
| − | \ | ||
| − | |||
| − | <math>\ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math>\ | ||
| − | |||
| − | \\ | ||
| − | |||
| − | \ | ||
| − | |||
| − | <math>\ | ||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | <math>\ | ||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | <math>\ | ||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | ( | ||
| − | |||
| − | ( | ||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | ( | ||
| − | |||
| − | ( | ||
| − | |||
| − | (( | ||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | (( | ||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | fzxy = z'(fx)(fy) | |
| − | + | ||
| − | + | ||
| − | + | F | |
| − | | | + | o |
| − | + | | | |
| − | + | o | |
| − | + | / \ | |
| − | + | o o | |
| − | + | o | |
| − | + | . | . | |
| − | | | + | . | . |
| − | + | . | . | |
| − | | | + | . o . |
| − | + | . / \ . | |
| − | + | . / \ . | |
| − | + | . / \ . | |
| − | + | . o o . | |
| − | + | . . . | |
| − | + | . . . | |
| − | + | . | |
| − | + | ||
| − | + | ||
| − | + | C o . / \ . o | |
| − | + | | . / \ . | CF | |
| − | + | | . o o . | | |
| − | + | f o . . . o fF | |
| − | + | / \ . . . / \ | |
| − | + | / . \ . o o | |
| − | + | X o o Y XF YF | |
| − | \ | + | |
| − | | | + | <u, v, w> in P -> |
| − | + | ||
| − | + | o---------o---------o---------o---------o | |
| − | + | | # h | h | f | | |
| − | + | o=========o=========o=========o=========o | |
| − | \\ | + | | P # X | Y | Z | |
| − | + | o---------o---------o---------o---------o | |
| − | \ | + | | Q # U | V | W | |
| − | + | o---------o---------o---------o---------o | |
| − | + | ||
| − | + | Products of diagonal extensions: | |
| − | < | + | |
| − | + | 1,1, = !1!!1! | |
| − | + | ||
| − | + | = "anything that is anything that is ---" | |
| − | + | ||
| − | + | = "anything that is ---" | |
| − | + | ||
| − | + | = !1! | |
| − | + | ||
| − | + | m,n = "man that is noble" | |
| − | + | ||
| − | + | = (C:C +, I:I +, J:J +, O:O)(C +, D +, O) | |
| − | + | ||
| − | + | = C +, O | |
| − | + | ||
| − | + | n,m = "noble that is man" | |
| − | + | ||
| − | + | = (C:C +, D:D +, O:O)(C +, I +, J +, O) | |
| − | + | ||
| − | | | + | = C +, O |
| − | + | ||
| − | + | n,w = "noble that is woman" | |
| − | + | ||
| − | + | = (C:C +, D:D +, O:O)(B +, D +, E) | |
| − | + | ||
| − | + | = D | |
| − | + | ||
| − | + | w,n = "woman that is noble" | |
| − | + | ||
| − | | | + | = (B:B +, D:D +, E:E)(C +, D +, O) |
| − | + | ||
| − | + | = D | |
| − | + | ||
| − | + | Given a set X and a subset M c X, define e_M, | |
| − | + | the "idempotent representation" of M over X, | |
| − | + | as the 2-adic relation e_M c X x X which is | |
| − | + | the identity relation on M. In other words, | |
| − | + | e_M = {<x, x> : x in M}. | |
| − | + | ||
| − | | | + | Transposing this by steps into Peirce's notation: |
| − | | | + | |
| − | + | e_M = {<x, x> : x in M} | |
| − | + | ||
| − | + | = {x:x : x in M} | |
| − | + | ||
| − | + | = Sum_X |x in M| x:x | |
| − | + | ||
| − | + | 'l' = "lover of ---" | |
| − | + | ||
| − | + | 's' = "servant of ---" | |
| − | + | ||
| − | + | 'l', = "lover that is --- of ---" | |
| − | + | ||
| − | + | 's', = "servant that is --- of ---" | |
| − | ( | + | |
| − | + | | But not only may any absolute term be thus regarded as a relative term, | |
| − | ( | + | | but any relative term may in the same way be regarded as a relative with |
| − | + | | one correlate more. It is convenient to take this additional correlate | |
| − | + | | as the first one. | |
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | Then: | |
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | 'l','s'w | |
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | will denote a lover of a woman that is a servant of that woman. | |
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | C.S. Peirce, CP 3.73 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | o---------o----+----o---------o---------o----+----o---------o | |
| + | o-----------------------------o-----------------------------o | ||
| + | | Objective Framework (OF) | Interpretive Framework (IF) | | ||
| + | o-----------------------------o-----------------------------o | ||
| + | | Objects | Signs | | ||
| + | o-----------------------------o-----------------------------o | ||
| + | | | | ||
| + | | C o--------------- | | ||
| + | | | | ||
| + | | F o--------------- | | ||
| + | | | | ||
| + | | I o--------------- | | ||
| + | | | | ||
| + | | O o--------------- | | ||
| + | | | | ||
| + | | B o--------------- | | ||
| + | | | | ||
| + | | D o--------------- | | ||
| + | | | | ||
| + | | E o--------------- | | ||
| + | | o "m" | | ||
| + | | / | | ||
| + | | / | | ||
| + | | / | | ||
| + | | o o o-----------@ | | ||
| + | | \ | | ||
| + | | \ | | ||
| + | | \ | | ||
| + | | o | | ||
| + | | | | ||
| + | o-----------------------------o-----------------------------o | ||
| − | + | †‡||§¶ | |
| + | @#||$% | ||
| − | + | quality, reflection, synecdoche | |
| − | + | 1. neglect of | |
| − | + | 2. neglect of | |
| − | + | 3. neglect of nil? | |
| − | + | ||
| − | + | Now, it's not the end of the story, of course, but it's a start. | |
| − | + | The significant thing is what is usually the significant thing | |
| − | + | in mathematics, at least, that two distinct descriptions refer | |
| − | + | to the same things. Incidentally, Peirce is not really being | |
| − | + | as indifferent to the distinctions between signs and things | |
| − | + | as this ascii text makes him look, but uses a host of other | |
| − | + | type-faces to distinguish the types and the uses of signs. | |
| − | + | </pre> | |
| − | + | ||
| − | + | ==Discussion Notes== | |
| − | + | ||
| − | + | ===Discussion Note 1=== | |
| − | | | + | |
| + | ; Gary Richmond | ||
| + | : I wonder if the necessary “elementary triad” spoken of below isn't somehow implicated in those discussions “invoking a <i>closure principle</i>”. | ||
| + | |||
| + | ; C.S. Peirce | ||
| + | : CP 1.292. It can further be said in advance, not, indeed, purely a priori but with the degree of apriority that is proper to logic, namely, as a necessary deduction from the fact that there are signs, that there must be an elementary triad. For were every element of the phaneron a monad or a dyad, without the relative of teridentity (which is, of course, a triad), it is evident that no triad could ever be built up. Now the relation of every sign to its object and interpretant is plainly a triad. A triad might be built up of pentads or of any higher perissad elements in many ways. But it can be proved — and really with extreme simplicity, though the statement of the general proof is confusing — that no element can have a higher valency than three. | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : (Of course this passage also directly relates to the recent thread on Identity and Teridentity.) | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Yes, generally speaking, I think that there are deep formal principles here that manifest themselves in these various guises: the levels of intention or the orders of reflection, the sign relation, pragmatic conceivability, the generative sufficiency of 3-adic relations for all practical intents, and the irreducibility of continuous relations. I have run into themes in combinatorics, group theory, and Lie algebras that are tantalizingly reminiscent of the things that Peirce says here, but it will take me some time to investigate them far enough to see what's going on. | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : PS. I came upon the above passage last night reading through the Peirce selections in John J. Stuhr's <i>Classical American Philosophy : Essential Readings and Interpretive Essays</i>, Oxford University, 1987 (the passage above is found on pp. 61–62), readily available in paperback in a new edition, I believe. | ||
| + | |||
| + | : An aside: These excerpts in Sturh include versions of a fascinating “Intellectual Autobiography”, Peirce's summary of his scientific, especially, philosophic accomplishments. I've seen them published nowhere else. | ||
| + | |||
| + | ===Discussion Note 2=== | ||
| + | |||
| + | ; Benjamin Udell | ||
| + | : I'm in the process of moving back to NYC and have had little opportunity to do more than glance through posts during the past few weeks, but this struck me because it sounds something I really would like to know about, but I didn't understand it: | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Notice that Peirce follows the mathematician's usual practice, then and now, of making the status of being an "individual" or a "universal" relative to a discourse in progress. I have come to appreciate more and more of late how radically different this "patchwork" or "piecewise" approach to things is from the way of some philosophers who seem to be content with nothing less than many worlds domination, which means that they are never content and rarely get started toward the solution of any real problem. Just my observation, I hope you understand. | ||
| + | |||
| + | ; Benjamin Udell | ||
| + | : "Many worlds domination", "nothing less than many worlds domination" -- as opposed to the patchwork or piecewise approach. What is many worlds domination? When I hear "many worlds" I think of Everett's Many Worlds interpretation of quantum mechanics. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Yes, it is a resonance of Edward, Everett, and All the Other Whos in Whoville, but that whole microcosm is itself but the frumious reverberation of Leibniz's Maenadolatry. More sequitur, though, this is an issue that has simmered beneath the surface of my consciousness for several decades now and only periodically percolates itself over the hyper-critical thrashold of expression. Let me see if I can a better job of it this time. The topic is itself a patchwork of infernally recurrent patterns. Here are a few pieces of it that I can remember arising recently: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\ | + | <p> |
| − | + | <b>Zeroth Law Of Semantics</b><br> | |
| − | + | <br> | |
| − | + | Meaning is a privilege not a right.<br> | |
| − | + | Not all pictures depict.<br> | |
| − | + | Not all signs denote.<br> | |
| − | \\ | + | <br> |
| − | + | Never confuse a property of a sign,<br> | |
| − | \ | + | for instance, existence,<br> |
| − | | | + | with a sign of a property,<br> |
| − | <math>\ | + | for instance, existence.<br> |
| − | ( | + | <br> |
| − | + | Taking a property of a sign,<br> | |
| − | ( | + | for a sign of a property,<br> |
| − | + | is the zeroth sign of<br> | |
| − | + | nominal thinking,<br> | |
| − | + | and the first<br> | |
| − | + | mistake.<br> | |
| − | \ | + | <br> |
| − | + | Also Sprach 0* | |
| − | <math> | + | </p> |
| − | + | |} | |
| − | \\ | + | |
| − | + | : A less catchy way of saying "meaning is a privilege not a right" would most likely be "meaning is a contingency not a necessity". But if I reflect on that phrase, it does not quite satisfy me, since a deeper lying truth is that contingency and necessity, connections in fact and connections beyond the reach of fact, depend on a line of distinction that is itself drawn on the scene of observation from the embodied, material, physical, non-point massive, non-purely-spectrelative point of view of an agent or community of interpretation, a discursive universe, an engauged interpretant, a frame of at least partial self-reverence, a hermeneutics in progress, or a participant observer. In short, this distinction between the contingent and the necessary is itself contingent, which means, among other things, that signs are always indexical at some least quantum. | |
| − | \\ | + | |
| − | + | ===Discussion Note 3=== | |
| − | \\ | + | |
| − | + | ; Joe Ransdell | |
| − | \ | + | : Would the Kripke conception of the "rigid designator" be an instance of the "many worlds domination"? I was struck by your speaking of the "patchwork or piecewise" approach as well in that it seemed to me you might be expressing the same general idea that I have usually thought of in terms of contextualism instead: I mean the limits it puts upon what you can say a priori if you really take contextualism seriously, which is the same as recognizing indexicality as incapable of elimination, I think. |
| − | + | ||
| − | <math> | + | ; Jon Awbrey |
| − | + | : Yes, I think this is the same ballpark of topics. I can't really speak for what Kripke had in mind, but I have a practical acquaintance with the way that some people have been trying to put notions like this to work on the applied ontology scene, and it strikes me as a lot of nonsense. I love a good parallel worlds story as much as anybody, but it strikes me that many worlds philosophers have the least imagination of anybody as to what an alternative universe might really be like and so I prefer to read more creative writers when it comes to that. But serially, folks, I think that the reason why some people evidently feel the need for such outlandish schemes — and the vast majority of the literature on counterfactual conditionals falls into the same spaceboat as this — is simply that they have failed to absorb, through the fault of Principian filters, a quality that Peirce's logic is thoroughly steeped in, namely, the functional interpretation of logical terms, that is, as signs referring to patterns of contingencies. It is why he speaks more often, and certainly more sensibly and to greater effect, of “conditional generals” than of “modal subjunctives”. This is also bound up with that element of sensibility that got lost in the transition from Peircean to Fregean quantifiers. Peirce's apriorities are always hedged with risky bets. | |
| − | \\ | + | |
| − | + | ===Discussion Note 4=== | |
| − | \\ | + | |
| − | + | ; Benjamin Udell | |
| − | \\ | + | : I wish I had more time to ponder the "many-worlds" issue (& that my books were not currently disappearing into heavily taped boxes). I had thought of the piecemeal approach's opposite as the attempt to build a kind of monolithic picture, e.g., to worry that there is not an infinite number of particles in the physical universe for the infinity integers. But maybe the business with rigid designators & domination of many worlds has somehow to do with monolithism. |
| − | + | ||
| − | \ | + | ; Jon Awbrey |
| − | + | : Yes, that's another way of saying it. When I look to my own priorities, my big worry is that logic as a discipline is not fulfilling its promise. I have worked in too many settings where the qualitative researchers and the quantitative researchers could barely even talk to one an Other with any understanding, and this I recognized as a big block to inquiry since our first notice of salient facts and significant phenomena is usually in logical, natural language, or qualitative forms, while our eventual success in resolving anomalies and solving practical problems depends on our ability to formalize, operationalize, and quantify the issues, even if only to a very partial degree, as it generally turns out. | |
| − | <math>\ | + | |
| − | ( | + | : When I look to the history of how logic has been deployed in mathematics, and through those media in science generally, it seems to me that the Piece Train started to go off track with the <i>Principia Mathematica</i>. All pokes in the rib aside, however, I tend to regard this event more as the symptom of a localized cultural phenomenon than as the root cause of the broader malaise. |
| − | \ | + | |
| − | + | ===Discussion Note 5=== | |
| − | \\ | + | |
| − | + | ; C.S. Peirce | |
| − | \\ | + | |
| − | ~\ | + | {| align="center" cellspacing="6" width="90%" |
| − | \ | + | | For example, |
| + | |- | ||
| + | | align="center" | <math>\mathrm{f} + \mathrm{u}\!</math> | ||
| + | |- | ||
| + | | means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are <i>besides themselves</i>. | ||
| + | |} | ||
| + | |||
| + | ; Clark Goble | ||
| + | : Could you clarify your use of “besides”? | ||
| + | |||
| + | : I think I am following your thinking in that you don't want the logical terms to be considered to have any necessary identity between them. Is that right? | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : I use vertical sidebars "|" for long quotations, so this is me quoting Peirce at CP 3.67 who is explaining in an idiomatic way Boole's use of the plus sign for a logical operation that is strictly speaking limited to terms for mutually exclusive classes. The operation would normally be extended to signify the “symmetric difference” operator. But Peirce is saying that he prefers to use the sign <math>{}^{\backprime\backprime} +\!\!, {}^{\prime\prime}</math> for inclusive disjunction, corresponding to the union of the associated classes. Peirce calls Boole's operation “invertible” because it amounts to the sum operation in a field, whereas the inclusive disjunction or union is “non-invertible”, since knowing that <math>A \cup B = C\!</math> does not allow one to say determinately that <math>A = C - B.\!</math> I can't recall if Boole uses this “besides” idiom, but will check later. | ||
| + | |||
| + | ===Discussion Note 6=== | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : I use vertical sidebars “|” for long quotations, so this is me quoting Peirce at CP 3.67 who is explaining in an idiomatic way Boole's use of the plus sign for a logical operation that is strictly speaking limited to terms for mutually exclusive classes. | ||
| + | |||
| + | ; Clark Goble | ||
| + | : Is that essay related to any of the essays in the two volume <i>Essential Peirce</i>? I'm rather interested in how he speaks there. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : No, the EP volumes are extremely weak on logical selections. I see nothing there that deals with the logic of relatives. | ||
| + | |||
| + | : But Peirce is saying that he prefers to use the sign <math>{}^{\backprime\backprime} +\!\!, {}^{\prime\prime}</math> for inclusive disjunction, corresponding to the union of the associated classes. | ||
| + | |||
| + | ; Clark Goble | ||
| + | : The reason I asked was more because it seemed somewhat interesting in light of the logic of operators in quantum mechanics. I was curious if the use of “beside” might relate to that. But from what you say it probably was just me reading too much into the quote. The issue of significance was whether the operation entailed the necessity of mutual exclusivity or whether some relationship between the classes might be possible. I kind of latched on to Peirce's odd statement about “all French violinists are <i>beside themselves</i>”. | ||
| + | |||
| + | : Did Peirce have anything to say about what we'd call non-commuting operators? | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : In general, 2-adic relative terms are non-commutative. For example, a brother of a mother is not identical to a mother of a brother. | ||
| + | |||
| + | ===Discussion Note 7=== | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : I am very much enjoying, which is to say, learning from your interlacing commentary on Peirce's 1870 “Logic of Relatives” paper. | ||
| + | |||
| + | : What an extraordinary paper the 1870 “LOR” is! Your notes helped me appreciate the importance of the unanticipated proposal of P's to “assign to all logical terms, numbers”. On the other hand, the excerpts suggested to we why Peirce finally framed his Logic of Relatives into graphical form. Still, I think that a thorough examination of the 1970 paper might serve as propaedeutic (and of course, much more) for the study of the alpha and beta graphs. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Yes, there's gold in them thar early logic papers that has been “panned” but nowhere near mined in depth yet. The whole quiver of arrows between terms and numbers harks back to the <i>numeri characteristici</i> of Leibniz, of course, but Leibniz attended more on the intensional chains of being while Peirce will here start to “escavate” the extensional hierarchies. | ||
| + | |||
| + | : I consider myself rewarded that you see the incipient impulse toward logical graphs, as one of the most striking things to me about this paper is to see these precursory seeds already planted here within it and yet to know how long it will take them to sprout and bloom. | ||
| + | |||
| + | : Peirce is obviously struggling to stay within the linotyper's art — a thing that we, for all our exorbitant hype about markable text, are still curiously saddled with — but I do not believe that it is possible for any mind equipped with a geometrical imagination to entertain these schemes for connecting up terminological hubs with their terminological terminals without perforce stretching imaginary strings between the imaginary gumdrops. | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : I must say though that the pace at which you've been throwing this at us is not to be kept up with by anyone I know “in person or by reputation”. I took notes on the first 5 or 6 Notes, but can now just barely find time to read through your posts. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Oh, I was trying to burrow as fast as I could toward the more untapped veins — I am guessing that things will probably “descalate” a bit over the next week, but then, so will our attention spans … | ||
| + | |||
| + | : Speaking of which, I will have to break here, and pick up the rest later … | ||
| + | |||
| + | ===Discussion Note 8=== | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : In any event, I wish that you'd comment on Note 5 more directly (though you do obliquely in your own diagramming of “every [US] Vice-President(s) … [who is] every President(s) of the US Senate”. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : There are several layers of things to say about that, and I think that it would be better to illustrate the issues by way of the examples that Peirce will soon be getting to, but I will see what I can speak to for now. | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : But what interested me even more in LOR, Note 5, was the sign <math>{}^{\backprime\backprime} < {}^{\prime\prime}\!</math> (“less than” joined to the sign of identity <math>{}^{\backprime\backprime} = {}^{\prime\prime}\!</math> to yield Peirce's famous sign <math>{}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!</math> (or more clearly, <math>{}^{\backprime\backprime} \texttt{=}\!\texttt{<} {}^{\prime\prime}\!</math>) of inference, which combines the two (so that <math>{}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!</math> (literally, “as small as”) means “is”. I must say I both “get” this and don't quite (Peirce's example(s) of the frenchman helped a little). Perhaps your considerably more mathematical mind can help clarify this for a non-mathematician such as myself. (My sense is that “as small as” narrows the terms so that “everything that occurs in the conclusion is already contained in the premise”.) I hope I'm not being obtuse here. I'm sure it's “all too simple for words”. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Then let us draw a picture. | ||
| + | |||
| + | : The proposition <math>\texttt{(} F ~ \texttt{(} G \texttt{))},\!</math> read as <math>{}^{\backprime\backprime} \mathrm{not}~ F ~\mathrm{without}~ G {}^{\prime\prime},\!</math> states that the region indicated by <math>F ~ \texttt{(} G \texttt{)},\!</math> in other words, where <math>F ~\mathrm{and~not}~ G\!</math> holds true, is the only region exempted from the occupation of being in this universe: | ||
| + | |||
| + | {| align="center" cellspacing="6" | ||
| | | | ||
| − | < | + | <pre> |
| − | + | o-----------------------------------------------------------o | |
| − | \\ | + | |`X`````````````````````````````````````````````````````````| |
| − | + | |```````````````````````````````````````````````````````````| | |
| − | \\ | + | |`````````````o-------------o```o-------------o`````````````| |
| − | + | |````````````/ \`/```````````````\````````````| | |
| − | \\ | + | |```````````/ o`````````````````\```````````| |
| − | + | |``````````/ /`\`````````````````\``````````| | |
| − | \ | + | |`````````/ /```\`````````````````\`````````| |
| − | | | + | |````````/ /`````\`````````````````\````````| |
| + | |```````o o```````o`````````````````o```````| | ||
| + | |```````| |```````|`````````````````|```````| | ||
| + | |```````| |```````|`````````````````|```````| | ||
| + | |```````| F |```````|````````G````````|```````| | ||
| + | |```````| |```````|`````````````````|```````| | ||
| + | |```````| |```````|`````````````````|```````| | ||
| + | |```````o o```````o`````````````````o```````| | ||
| + | |````````\ \`````/`````````````````/````````| | ||
| + | |`````````\ \```/`````````````````/`````````| | ||
| + | |``````````\ \`/`````````````````/``````````| | ||
| + | |```````````\ o`````````````````/```````````| | ||
| + | |````````````\ /`\```````````````/````````````| | ||
| + | |`````````````o-------------o```o-------------o`````````````| | ||
| + | |```````````````````````````````````````````````````````````| | ||
| + | |```````````````````````````````````````````````````````````| | ||
| + | o-----------------------------------------------------------o | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | : Collapsing the vacuous region like soapfilm popping on a wire frame, we draw the constraint <math>\texttt{(} F ~ \texttt{(} G \texttt{))}\!</math> in the following alternative fashion: | ||
| + | |||
| + | {| align="center" cellspacing="6" | ||
| | | | ||
| − | < | + | <pre> |
| − | + | o-----------------------------------------------------------o | |
| − | \\ | + | |`X`````````````````````````````````````````````````````````| |
| − | + | |```````````````````````````````````````````````````````````| | |
| − | \ | + | |```````````````````````````````o-------------o`````````````| |
| − | + | |``````````````````````````````/```````````````\````````````| | |
| − | <math>\ | + | |`````````````````````````````o`````````````````\```````````| |
| − | + | |````````````````````````````/`\`````````````````\``````````| | |
| − | \\ | + | |```````````````````````````/```\`````````````````\`````````| |
| − | + | |``````````````````````````/`````\`````````````````\````````| | |
| − | + | |`````````````````````````o```````o`````````````````o```````| | |
| + | |`````````````````````````|```````|`````````````````|```````| | ||
| + | |`````````````````````````|```````|`````````````````|```````| | ||
| + | |`````````````````````````|```F```|````````G````````|```````| | ||
| + | |`````````````````````````|```````|`````````````````|```````| | ||
| + | |`````````````````````````|```````|`````````````````|```````| | ||
| + | |`````````````````````````o```````o`````````````````o```````| | ||
| + | |``````````````````````````\`````/`````````````````/````````| | ||
| + | |```````````````````````````\```/`````````````````/`````````| | ||
| + | |````````````````````````````\`/`````````````````/``````````| | ||
| + | |`````````````````````````````o`````````````````/```````````| | ||
| + | |``````````````````````````````\```````````````/````````````| | ||
| + | |```````````````````````````````o-------------o`````````````| | ||
| + | |```````````````````````````````````````````````````````````| | ||
| + | |```````````````````````````````````````````````````````````| | ||
| + | o-----------------------------------------------------------o | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | : So all of the following expressions, under suitable mutations of interpretation, are just so many ways of saying that the denotation of <math>{}^{\backprime\backprime} F {}^{\prime\prime}\!</math> is contained within the denotation of <math>{}^{\backprime\backprime} G {}^{\prime\prime}.\!</math> | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{l} |
| − | ~\ | + | \texttt{(} F ~ \texttt{(} G \texttt{))} |
\\[4pt] | \\[4pt] | ||
| − | + | F \Rightarrow G | |
| − | |||
| − | |||
| − | |||
| − | |||
\\[4pt] | \\[4pt] | ||
| − | + | F ~\texttt{=}\!\texttt{<}~ G | |
| − | |||
| − | |||
| − | |||
| − | |||
\\[4pt] | \\[4pt] | ||
| − | ~\ | + | F ~\texttt{-}\!\texttt{<}~ G |
| − | |||
| − | |||
| − | |||
| − | |||
\\[4pt] | \\[4pt] | ||
| − | + | F \subseteq G | |
| − | \ | + | \end{array}\!</math> |
| − | | | + | |} |
| + | |||
| + | : Let us now look to the “characteristic functions” or “indicator functions” of the various regions of being. It is frequently convenient to use the same letters for them and merely to keep a variant interpretation “en-thy-meme”, but let us be more meticulous here, and reserve the corresponding lower case letters <math>f\!</math> and <math>g\!</math> to denote the indicator functions of the regions <math>F\!</math> and <math>G,\!</math> respectively. | ||
| + | |||
| + | : Taking <math>\mathbb{B} = \{ 0, 1 \}~\!</math> as the boolean domain, we have: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{lcl} |
| − | + | f, g : X & \to & \mathbb{B} | |
\\[4pt] | \\[4pt] | ||
| − | + | f^{-1}(1) & = & F | |
| − | |||
| − | |||
| − | |||
| − | |||
\\[4pt] | \\[4pt] | ||
| − | ( | + | g^{-1}(1) & = & G |
| − | \end{ | + | \end{array}\!</math> |
| + | |} | ||
| + | |||
| + | : In general, for a proposition <math>h : X \to \mathbb{B},\!</math> an expression like <math>h^{-1}(1)\!</math> can be read as “the inverse of <math>h\!</math> evaluated at <math>1\!</math>”, in effect, denoting the set of points in <math>X\!</math> where <math>h\!</math> evaluates to <math>\mathrm{true}.\!</math> This is called the “fiber of truth” under <math>h,\!</math> and I have gotten where I like to abbreviate it as <math>[|h|].\!</math> | ||
| + | |||
| + | : Accordingly, we have: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{*{7}{l}} |
| − | + | F & = & [|f|] & = & f^{-1}(1) & \subseteq & X | |
\\[4pt] | \\[4pt] | ||
| − | ( | + | G & = & [|g|] & = & g^{-1}(1) & \subseteq & X |
| − | \ | + | \end{array}\!</math> |
| + | |} | ||
| + | |||
| + | : This brings us to the question, what sort of “functional equation” between <math>f\!</math> and <math>g\!</math> goes with the regional constraint <math>\texttt{(} F ~ \texttt{(} G \texttt{))}\!</math>? | ||
| + | |||
| + | : Just this, that <math>f(x) ~\texttt{=}\!\texttt{<}~ g(x)\!</math> for all <math>x\!</math> in <math>X,\!</math> where the <math>{}^{\backprime\backprime} \texttt{=}\!\texttt{<} {}^{\prime\prime}\!</math> relation on the values in <math>\mathbb{B}\!</math> has the following operational table for the pairing <math>{}^{\backprime\backprime} \mathrm{row~head} ~\texttt{=}\!\texttt{<}~ \mathrm{column~head} {}^{\prime\prime}.\!</math> | ||
| + | |||
| + | {| align="center" cellspacing="6" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{|c||cc|} |
| − | + | \hline | |
| − | \\ | + | \texttt{=}\!\texttt{<} & 0 & 1 \\ |
| − | + | \hline\hline | |
| − | \ | + | 0 & 1 & 1 \\ |
| − | + | 1 & 0 & 1 \\ | |
| − | <math>\ | + | \hline |
| − | + | \end{array}\!</math> | |
| − | \\ | + | |} |
| − | ~ | + | |
| − | \ | + | : And this, of course, is the same thing as the truth table for the conditional connective or the implication relation. |
| − | + | ||
| − | <math>\ | + | ; Gary Richmond |
| − | + | : By the way, in the semiosis implied by the modal gamma graphs, could <math>{}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!</math> (were it used there, which of course it is not) ever be taken to mean “leads to” or “becomes” or “evolves into”? I informally use it that way myself, using the ordinary arrow for implication. | |
| − | \\ | + | |
| − | + | ; Jon Awbrey | |
| − | \ | + | : I am a bit insensitive to the need for modal logic, since necessity in mathematics always seems to come down to being a matter of truth for all actual cases, if under an expanded sense of actuality that makes it indiscernible from possibility, so I must beg off here. But there are places where Peirce makes a big deal about the advisability of drawing the <math>{}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!</math> symbol in one fell stroke of the pen, kind of like a “lazy gamma” — an old texican cattle brand — and I have seen another place where he reads <math>A ~\texttt{-}\!\texttt{<}~ B\!</math> as <math>{}^{\backprime\backprime} A, ~\text{in every way that it can be, is}~ B {}^{\prime\prime},\!</math> as if this <math>{}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!</math> fork in the road led into a veritable garden of branching paths. |
| − | | | + | |
| + | : And out again … | ||
| + | |||
| + | ===Discussion Note 9=== | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : I am a bit insensitive to the need for modal logic, since necessity in mathematics always seems to come down to being a matter of truth for all actual cases, if under an expanded sense of actuality that makes it indiscernible from possibility, so I must beg off here. | ||
| + | |||
| + | ; Gary Richmond | ||
| + | : I cannot agree with you regarding modal logic. Personally I feel that the gamma part of the EGs is of the greatest interest and potential importance, and as Jay Zeman has made clear in his dissertation, Peirce certainly thought this as well. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : You disagree that I am insensitive? Well, certainly nobody has ever done that before! No, I phrased it that way to emphasize the circumstance that it ever hardly comes up as an issue within the limited purview of my experience, and when it does — as in topo-logical boundary situations — it seems to require a sort of analysis that doesn't comport all that well with the classical modes and natural figures of speech about it. Then again, I spent thirty years trying to motorize Alpha, have only a few good clues how I would go about Beta, and so Gamma doesn't look like one of those items on my plate. | ||
| + | |||
| + | : Speeching Of Which --- | ||
| + | : Best Of The Season ... | ||
| + | : And Happy Trailing ... | ||
| + | |||
| + | ===Discussion Note 10=== | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : Thanks for your very informative talk. There is a point that I did not understand in Note 35: | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : If we operate in accordance with Peirce's example of <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> as the “giver of a horse to an owner of that horse”, then we may assume that the associative law and the distributive law are by default in force, allowing us to derive this equation: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{lll} |
| − | + | \mathit{l},\!\mathit{s}\mathrm{w} | |
| − | \\[ | + | & = & |
| − | + | \mathit{l},\!\mathit{s}(\mathrm{B} ~~+\!\!,~~ \mathrm{D} ~~+\!\!,~~ \mathrm{E}) | |
| − | \end{ | + | \\[6pt] |
| − | | | + | & = & |
| − | <math>\ | + | \mathit{l},\!\mathit{s}\mathrm{B} ~~+\!\!,~~ \mathit{l},\!\mathit{s}\mathrm{D} ~~+\!\!,~~ \mathit{l},\!\mathit{s}\mathrm{E} |
| − | ( | + | \end{array}</math> |
| − | \\ | + | |} |
| − | + | ||
| − | \ | + | ; Bernard Morand |
| + | : May be because language or more probably my lack of training in logic, what does mean that “associative law and distributive law are by default in force”? | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Those were some tricky Peirces, and I was trying to dodge them as artful as could be, but now you have fastly apprehended me! | ||
| + | |||
| + | : It may be partly that I left out the initial sections of this paper where Peirce discusses how he will regard the ordinarily applicable principles in the process of trying to extend and generalize them (CP 3.45–62), but there may be also an ambiguity in Peirce's use of the phrase “absolute conditions” (CP 3.62–68). Does he mean “absolutely necessary”, “indispensable”, “inviolate”, or does he mean “the conditions applying to the logic of absolute terms”, in which latter case we would expect to alter them sooner or later? | ||
| + | |||
| + | : We lose the commutative law, <math>xy = yx,\!</math> as soon as we extend to 2-adic relations, but keep the associative law, <math>x(yz) = (xy)z,\!</math> as the multiplication of 2-adics is the logical analogue of ordinary matrix multiplication, and Peirce like most mathematicians treats the double distributive law, <math>x(y + z) = xy + xz\!</math> and <math>(x + y)z = xz + yz,\!</math> and as something that must be striven to preserve as far as possible. | ||
| + | |||
| + | : Strictly speaking, Peirce is already using a principle that goes beyond the ordinary associative law, but that is recognizably analogous to it, for example, in the modified Othello case, where <math>(\mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{D})(\mathrm{J}\!:\!\mathrm{D})(\mathrm{D}) = \mathrm{J}.\!</math> | ||
| + | |||
| + | : If it were strictly associative, then we would have the following: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{lcccc} |
| − | + | (J:J:D)((J:D)(D)) & = & (J:J:D)(J) & = & 0? | |
\\[4pt] | \\[4pt] | ||
| − | ( | + | ((J:J:D)(J:D))(D) & = & (J)(D) & = & 0? |
| − | \end{ | + | \end{array}</math> |
| − | | | + | |} |
| − | <math>\ | + | |
| − | + | : In other words, the intended relational linkage would be broken. However, the type of product that Peirce is taking for granted in this situation often occurs in mathematics in just this way. There is another location where he comments more fully on this, but I have the sense that it was a late retrospective remark, and I do not recall if it was in CP or in the microfilm MSs that I read it. | |
| − | \\ | + | |
| − | + | : By “default” conditions I am referring more or less to what Peirce says at the end of CP 3.69, where he use an argument based on the distributive principle to rationalize the idea that “<i>A term multiplied by two relatives shows that the same individual is in the two relations.</i>” This means, for example, that one can let <math>{}^{\backprime\backprime} \mathfrak{g}\mathit{o}\mathrm{h} {}^{\prime\prime}\!</math>, without subjacent marks or numbers, be interpreted on the default convention of “overlapping scopes”, where the two correlates of <math>\mathfrak{g}\!</math> are given by the next two terms in line, namely, <math>\mathit{o}\!</math> and <math>\mathrm{h},\!</math> and the single correlate of <math>\mathit{o}\!</math> is given by the very next term in line, namely, <math>\mathrm{h}.\!</math> Thus, it is only when this natural scoping cannot convey the intended sense that we have to use more explicit mark-up devices. | |
| − | \ | + | |
| + | ; Bernard Morand | ||
| + | : About another point: do you think that the LOR could be of some help to solve the puzzle of the “second way of dividing signs” where CSP concludes that 66 classes could be made out of the 10 divisions (Letters to lady Welby)? (As I see them, the ten divisions involve a mix of relative terms, dyadic relations, and a triadic one. In order to make 66 classes it is clear that these 10 divisions have to be stated under some linear order. The nature of this order is at the bottom of the disagreements on the subject). | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : This topic requires a longer excuse from me than I am able to make right now, but maybe I'll get back to it later today or tomorrow. | ||
| + | |||
| + | ===Discussion Note 11=== | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : About another point: do you think that the LOR could be of some help to solve the puzzle of the "second way of dividing signs" where CSP concludes that 66 classes could be made out of the 10 divisions (Letters to lady Welby)? (As I see them, the ten divisions involve a mix of relative terms, dyadic relations and a triadic one. In order to make 66 classes it is clear that these 10 divisions have to be stated under some linear order. The nature of this order is at the bottom of the disagreements on the subject). | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Yes. At any rate, I have a pretty clear sense from reading Peirce's work in the period 1865–1870 that the need to understand the function of signs in scientific inquiry is one of the main reasons he found himself forced to develop both the theory of information and the logic of relatives. | ||
| + | |||
| + | : Peirce's work of this period is evenly distributed across the extensional and intensional pans of the balance in a way that is very difficult for us to follow anymore. I remember when I started looking into this I thought of myself as more of an "intensional, synthetic" than an "extensional, analytic" type of thinker, but that seems like a long time ago, as it soon became clear that much less work had been done in the Peirce community on the extensional side of things, while that was the very facet that needed to be polished up in order to reconnect logic with empirical research and mathematical models. So I fear that I must be content that other able people are working on the intensional classification of sign relations. | ||
| + | |||
| + | : Still, the way that you pose the question is very enticing, so maybe it is time for me to start thinking about this aspect of sign relations again, if you could say more about it. | ||
| + | |||
| + | ===Discussion Note 12=== | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : The pairing “intensional, synthetic” against the other “extensional, analytic” is not one that I would have thought so. I would have paired synthetic with extensional because synthesis consists in adding new facts to an already made conception. On the other side analysis looks to be the determination of features while neglecting facts. But may be there is something like a symmetry effect leading to the same view from two different points. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Oh, it's not too important, as I don't put a lot of faith in such divisions, and the problem for me is always how to integrate the facets of the object, or the faculties of the mind — but there I go being synthetic again! | ||
| + | |||
| + | : I was only thinking of a conventional contrast that used to be drawn between different styles of thinking in mathematics, typically one points to Descartes, and the extensionality of analytic geometry, versus Desargues, and the intensionality of synthetic geometry. | ||
| + | |||
| + | : It may appear that one has side-stepped the issue of empiricism that way, but then all that stuff about the synthetic à priori raises its head, and we have Peirce's insight that mathematics is observational and even experimental, and so I must trail off into uncoordinated elliptical thoughts … | ||
| + | |||
| + | : The rest I have to work at a while, and maybe go back to the Welby letters. | ||
| + | |||
| + | ===Discussion Note 13=== | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : I will try to make clear the matter, at least as far as I understand it for now. We can summarize in a table the 10 divisions with their number in a first column, their title in current (peircean) language in the second and some kind of logical notation in the third. The sources come mainly from the letters to Lady Welby. While the titles come from CP 8.344, the third column comes from my own interpretation. | ||
| + | |||
| + | : So we get: | ||
| + | |||
| + | {| align="center" cellspacing="6" | ||
| | | | ||
| − | < | + | <pre> |
| − | + | I - According to the Mode of Apprehension of the Sign itself - S | |
| − | + | II - According to the Mode of Presentation of the Immediate Object - Oi | |
| − | + | III - According to the Mode of Being of the Dynamical Object - Od | |
| − | + | IV - According to the Relation of the Sign to its Dynamical Object - S-Od | |
| − | + | V - According to the Mode of Presentation of the Immediate Interpretant - Ii | |
| − | + | VI - According to the Mode of Being of the Dynamical Interpretant - Id | |
| − | + | VII - According to the relation of the Sign to the Dynamical Interpretant - S-Id | |
| − | + | VIII - According to the Nature of the Normal Interpretant - If | |
| − | + | IX - According to the the relation of the Sign to the Normal Interpretant - S-If | |
| − | + | X - According to the Triadic Relation of the Sign to its Dynamical Object | |
| − | + | and to its Normal Interpretant - S-Od-If | |
| − | + | </pre> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | ; Jon Awbrey | |
| + | : For my future study, I will reformat the table in a way that I can muse upon. I hope the roman numerals have not become canonical, as I cannot abide them. | ||
| − | {| align="center | + | {| align="center" cellspacing="6" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | < | + | <pre> |
| − | + | Table. Ten Divisions of Signs (Peirce, Morand) | |
| − | + | o---o---------------o------------------o------------------o---------------o | |
| − | + | | | According To: | Of: | To: | | | |
| − | + | o===o===============o==================o==================o===============o | |
| − | + | | 1 | Apprehension | Sign Itself | | S | | |
| − | + | | 2 | Presentation | Immediate Object | | O_i | | |
| − | + | | 3 | Being | Dynamical Object | | O_d | | |
| − | + | | 4 | Relation | Sign | Dynamical Object | S : O_d | | |
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | | 5 | Presentation | Immediate Interp | | I_i | | ||
| + | | 6 | Being | Dynamical Interp | | I_d | | ||
| + | | 7 | Relation | Sign | Dynamical Interp | S : I_d | | ||
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | | 8 | Nature | Normal Interp | | I_f | | ||
| + | | 9 | Relation | Sign | Normal Interp | S : I_f | | ||
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | | A | Relation | Sign | Dynamical Object | | | ||
| + | | | | | & Normal Interp | S : O_d : I_f | | ||
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | : Just as I have always feared, this classification mania appears to be communicable! But now I must definitely review the Welby correspondence, as all this stuff was a blur to my sensibilities the last 10 times I read it. | ||
| + | |||
| + | ===Discussion Note 14=== | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | {| align="center" cellspacing="6" | ||
| | | | ||
| − | < | + | <pre> |
| − | ( | + | Table. Ten Divisions of Signs (Peirce, Morand) |
| − | \\ | + | o---o---------------o------------------o------------------o---------------o |
| − | ( | + | | | According To: | Of: | To: | | |
| − | + | o===o===============o==================o==================o===============o | |
| − | + | | 1 | Apprehension | Sign Itself | | S | | |
| − | \\ | + | | 2 | Presentation | Immediate Object | | O_i | |
| − | + | | 3 | Being | Dynamical Object | | O_d | | |
| − | \ | + | | 4 | Relation | Sign | Dynamical Object | S : O_d | |
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | | 5 | Presentation | Immediate Interp | | I_i | | ||
| + | | 6 | Being | Dynamical Interp | | I_d | | ||
| + | | 7 | Relation | Sign | Dynamical Interp | S : I_d | | ||
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | | 8 | Nature | Normal Interp | | I_f | | ||
| + | | 9 | Relation | Sign | Normal Interp | S : I_f | | ||
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | | A | Relation | Sign | Dynamical Object | | | ||
| + | | | | | & Normal Interp | S : O_d : I_f | | ||
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : Yes this is clearer (in particular in expressing relations with “:”) | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : This is what Peirce used to form elementary relatives, for example, <math>o\!:\!s\!:\!i = (o, s, i),\!</math> and I find it utterly ubertous in a wide variety of syntactic circumstances. | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : I suggest making a correction to myself if the table is destinate to become canonic. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Hah! Good one! | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : I probably made a too quick jump from Normal Interpretant to Final Interpretant. As we know, the final interpretant, the ultimate one is not a sign for Peirce but a habit. So for the sake of things to come it would be more careful to retain <math>\mathrm{I_n}\!</math> in place of <math>\mathrm{I_f}\!</math> for now. | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : This accords with my understanding of how the word is used in mathematics. In my own work it has been necessary to distinguish many different species of expressions along somewhat similar lines, for example: arbitrary, basic, canonical, decidable, normal, periodic, persistent, prototypical, recurrent, representative, stable, typical, and so on. So I will make the changes below: | ||
| + | |||
| + | {| align="center" cellspacing="6" | ||
| | | | ||
| − | < | + | <pre> |
| − | + | Table. Ten Divisions of Signs (Peirce, Morand) | |
| − | + | o---o---------------o------------------o------------------o---------------o | |
| − | + | | | According To: | Of: | To: | | | |
| − | + | o===o===============o==================o==================o===============o | |
| − | + | | 1 | Apprehension | Sign Itself | | S | | |
| − | + | | 2 | Presentation | Immediate Object | | O_i | | |
| − | + | | 3 | Being | Dynamical Object | | O_d | | |
| − | + | | 4 | Relation | Sign | Dynamical Object | S : O_d | | |
| − | + | o---o---------------o------------------o------------------o---------------o | |
| − | < | + | | 5 | Presentation | Immediate Interp | | I_i | |
| − | + | | 6 | Being | Dynamical Interp | | I_d | | |
| − | + | | 7 | Relation | Sign | Dynamical Interp | S : I_d | | |
| − | + | o---o---------------o------------------o------------------o---------------o | |
| − | + | | 8 | Nature | Normal Interp | | I_n | | |
| − | + | | 9 | Relation | Sign | Normal Interp | S : I_n | | |
| − | + | o---o---------------o------------------o------------------o---------------o | |
| − | + | | A | Tri. Relation | Sign | Dynamical Object | | | |
| − | + | | | | | & Normal Interp | S : O_d : I_n | | |
| + | o---o---------------o------------------o------------------o---------------o | ||
| + | </pre> | ||
| + | |} | ||
| + | |||
| + | ; Bernard Morand | ||
| + | : Peirce gives the following definition (CP 8.343). | ||
| + | |||
| + | ; C.S. Peirce | ||
| + | : It is likewise requisite to distinguish the <i>Immediate Interpretant</i>, i.e. the Interpretant represented or signified in the Sign, from the <i>Dynamic Interpretant</i>, or effect actually produced on the mind by the Sign; and both of these from the <i>Normal Interpretant</i>, or effect that would be produced on the mind by the Sign after sufficient development of thought. (<i>Collected Papers</i>, CP 8.343). | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : Well, you've really tossed me in the middle of the briar patch now! I must continue with my reading from the 1870 LOR, but now I have to add to my do-list the problems of comparing the whole variorum of letters and drafts of letters to Lady Welby. I have only the CP 8 and Wiener versions here, so I will depend on you for ample excerpts from the Lieb volume. | ||
| + | |||
| + | ===Discussion Note 15=== | ||
| + | |||
| + | ; Jon Awbrey | ||
| + | : I will need to go back and pick up the broader contexts of your quotes. For ease of study I break Peirce's long paragraphs into smaller pieces. | ||
| + | |||
| + | ; C.S. Peirce | ||
| + | {| align="center" width="90%" | ||
| | | | ||
| − | < | + | <p>It seems to me that one of the first useful steps toward a science of <i>semeiotic</i> (<i>σημειωτική</i>), or the cenoscopic science of signs, must be the accurate definition, or logical analysis, of the concepts of the science.</p> |
| − | + | ||
| − | + | <p>I define a <i>Sign</i> as anything which on the one hand is so determined by an Object and on the other hand so determines an idea in a person's mind, that this latter determination, which I term the <i>Interpretant</i> of the sign, is thereby mediately determined by that Object.</p> | |
| − | + | ||
| − | + | <p>A sign, therefore, has a triadic relation to its Object and to its Interpretant. But it is necessary to distinguish the <i>Immediate Object</i>, or the Object as the Sign represents it, from the <i>Dynamical Object</i>, or really efficient but not immediately present Object.</p> | |
| − | + | ||
| − | + | <p>It is likewise requisite to distinguish the <i>Immediate Interpretant</i>, i.e. the Interpretant represented or signified in the Sign, from the <i>Dynamic Interpretant</i>, or effect actually produced on the mind by the Sign; and both of these from the <i>Normal Interpretant</i>, or effect that would be produced on the mind by the Sign after sufficient development of thought.</p> | |
| − | + | ||
| − | + | <p>On these considerations I base a recognition of ten respects in which Signs may be divided. I do not say that these divisions are enough. But since every one of them turns out to be a trichotomy, it follows that in order to decide what classes of signs result from them, I have 3<sup>10</sup>, or 59049, difficult questions to carefully consider; and therefore I will not undertake to carry my systematical division of signs any further, but will leave that for future explorers.</p> | |
| − | + | ||
| − | < | + | <p>(<i>Collected Papers</i>, CP 8.343).</p> |
| − | ( | + | |} |
| − | + | ||
| − | + | ; Jon Awbrey | |
| − | + | : You never know when the future explorer will be yourself. | |
| − | + | ||
| − | + | ===Discussion Note 16=== | |
| − | + | ||
| − | + | <pre> | |
| − | |- | + | Burks, the editor of CP 8, attaches this footnote |
| + | to CP 8.342-379, "On the Classification of Signs": | ||
| + | |||
| + | | From a partial draft of a letter to Lady Welby, bearing | ||
| + | | the dates of 24, 25, and 28 December 1908, Widener IB3a, | ||
| + | | with an added quotation in 368n23. ... | ||
| + | |||
| + | There is a passage roughly comparable to CP 8.343 in a letter | ||
| + | to Lady Welby dated 23 December 1908, pages 397-409 in Wiener, | ||
| + | which is incidentally the notorious "sop to Cerberus" letter: | ||
| + | |||
| + | | It is usual and proper to distinguish two Objects of a Sign, | ||
| + | | the Mediate without, and the Immediate within the Sign. Its | ||
| + | | Interpretant is all that the Sign conveys: acquaintance with | ||
| + | | its Object must be gained by collateral experience. | ||
| | | | ||
| − | + | | The Mediate Object is the Object outside of the Sign; I call | |
| − | + | | it the 'Dynamoid' Object. The Sign must indicate it by a hint; | |
| − | + | | and this hint, or its substance, is the 'Immediate' Object. | |
| − | |||
| − | |||
| | | | ||
| − | + | | Each of these two Objects may be said to be capable of either of | |
| − | + | | the three Modalities, though in the case of the Immediate Object, | |
| − | + | | this is not quite literally true. | |
| − | |||
| − | |||
| | | | ||
| − | + | | Accordingly, the Dynamoid Object may be a Possible; when I term | |
| − | + | | the Sign an 'Abstractive'; such as the word Beauty; and it will be | |
| − | + | | none the less an Abstractive if I speak of "the Beautiful", since it is | |
| − | + | | the ultimate reference, and not the grammatical form, that makes the sign | |
| − | + | | an 'Abstractive'. | |
| | | | ||
| − | + | | When the Dynamoid Object is an Occurrence (Existent thing or Actual fact | |
| − | + | | of past or future), I term the Sign a 'Concretive'; any one barometer | |
| − | + | | is an example; and so is a written narrative of any series of events. | |
| − | |||
| − | |||
| | | | ||
| − | + | | For a 'Sign' whose Dynamoid Object is a Necessitant, I have at present | |
| − | + | | no better designation than a 'Collective', which is not quite so bad a | |
| − | + | | name as it sounds to be until one studies the matter: but for a person, | |
| − | + | | like me, who thinks in quite a different system of symbols to words, it | |
| − | + | | is so awkward and often puzzling to translate one's thought into words! | |
| | | | ||
| − | + | | If the Immediate Object is a "Possible", that is, if the Dynamoid Object | |
| − | + | | is indicated (always more or less vaguely) by means of its Qualities, etc., | |
| − | + | | I call the Sign a 'Descriptive'; | |
| − | |||
| − | |||
| − | | | ||
| | | | ||
| − | + | | if the Immediate is an Occurrence, I call the Sign a 'Designative'; | |
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | and if the Immediate Object is a Necessitant, I call the Sign a | |
| − | + | | 'Copulant'; for in that case the Object has to be so identified | |
| − | + | | by the Interpreter that the Sign may represent a necessitation. | |
| − | + | | My name is certainly a temporary expedient. | |
| − | |||
| | | | ||
| − | + | | It is evident that a possible can determine nothing but a Possible, | |
| − | + | | it is equally so that a Necessitant can be determined by nothing but | |
| − | + | | a Necessitant. Hence it follows from the Definition of a Sign that | |
| − | + | | since the Dynamoid Object determines the Immediate Object, | |
| − | |||
| | | | ||
| − | + | | Which determines the Sign itself, | |
| − | + | | which determines the Destinate Interpretant | |
| − | + | | which determines the Effective Interpretant | |
| − | + | | which determines the Explicit Interpretant | |
| − | |||
| | | | ||
| − | + | | the six trichotomies, instead of determining 729 classes of signs, | |
| − | ( | + | | as they would if they were independent, only yield 28 classes; |
| − | + | | and if, as I strongly opine (not to say almost prove), there | |
| − | + | | are four other trichotomies of signs of the same order of | |
| − | + | | importance, instead of making 59,049 classes, these will | |
| + | | only come to 66. | ||
| | | | ||
| − | + | | The additional 4 trichotomies are undoubtedly, first: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | Icons*, Symbols, Indices, | |
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | |*(or Simulacra, Aristotle's 'homoiomata'), caught from Plato, who I guess took it | |
| − | ( | + | | from the Mathematical school of logic, for it earliest appears in the 'Phaedrus' |
| − | + | | which marks the beginning of Plato's being decisively influenced by that school. | |
| − | + | | Lutoslowski is right in saying that the 'Phaedrus' is later than the 'Republic' | |
| − | + | | but his date 379 B.C. is about eight years too early. | |
| | | | ||
| − | + | | and then 3 referring to the Interpretants. One of these I am pretty confident | |
| − | + | | is into: 'Suggestives', 'Imperatives', 'Indicatives', where the Imperatives | |
| − | + | | include the Interrogatives. Of the other two I 'think' that one must be | |
| − | + | | into Signs assuring their Interpretants by: | |
| − | |||
| | | | ||
| − | + | | Instinct, Experience, Form. | |
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | The other I suppose to be what, in my 'Monist' | |
| − | + | | exposition of Existential Graphs, I called: | |
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | | Semes, Phemes, Delomes. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| | | | ||
| − | + | | CSP, 'Selected Writings', pp. 406-408. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | |'Charles S. Peirce: Selected Writings (Values in a Universe of Chance)', | |
| − | + | | edited with an introduction and notes by Philip P. Wiener, Dover, | |
| − | + | | New York, NY, 1966. Originally published under the subtitle | |
| − | + | | in parentheses above, Doubleday & Company, 1958. | |
| − | + | ||
| − | + | But see CP 4.549-550 for a significant distinction between | |
| − | + | the categories (or modalities) and the orders of intention. | |
| − | + | </pre> | |
| − | + | ||
| − | | | + | ===Discussion Note 17=== |
| − | + | ||
| − | + | <pre> | |
| − | + | HC = Howard Callaway | |
| − | + | JA = Jon Awbrey | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | JA: In closing, observe that the teridentity relation has turned up again | |
| + | in this context, as the second comma-ing of the universal term itself: | ||
| − | = | + | 1,, = B:B:B +, C:C:C +, D:D:D +, E:E:E +, I:I:I +, J:J:J +, O:O:O. |
| − | + | HC: I see that you've come around to a mention of teridentity again, Jon. | |
| + | Still, if I recall the prior discussions, then no one doubts that we | ||
| + | can have a system of notation in which teridentity appears (I don't | ||
| + | actually see it here). | ||
| − | + | Perhaps we could get at the root of the misunderstanding | |
| + | if you tell me why you don't actually see the concept of | ||
| + | teridentity being exemplified here. | ||
| − | + | If it's only a matter of having lost the context of the | |
| + | present discussion over the break, then you may find the | ||
| + | previous notes archived at the distal ends of the ur-links | ||
| + | that I append below (except for the first nine discussion | ||
| + | notes that got lost in a disk crash at the Arisbe Dev site). | ||
| − | + | HC: Also, I think we can have a system of notation in which | |
| + | teridentity is needed. Those points seem reasonably clear. | ||
| − | + | The advantage of a concept is the integration of a species of manifold. | |
| − | + | The necessity of a concept is the incapacity to integrate it otherwise. | |
| − | + | ||
| − | + | Of course, no one should be too impressed with a concept that | |
| − | + | is only the artifact of a particular system of representation. | |
| − | + | So before we accord a concept the status of addressing reality, | |
| − | + | and declare it a term of some tenured office in our intellects, | |
| − | + | we would want to see some evidence that it helps us to manage | |
| − | + | a reality that we cannot see a way to manage any other way. | |
| − | + | ||
| − | + | Granted. | |
| − | + | ||
| − | + | Now how in general do we go about an investiture of this sort? | |
| − | + | That is the big question that would serve us well to consider | |
| − | + | in the process of the more limited investigation of identity. | |
| − | + | Indeed, I do not see how it is possible to answer the small | |
| − | + | question if no understanding is reached on the big question. | |
| − | + | ||
| − | + | HC: What remains relatively unclear is why we should need a system of notation | |
| − | + | in which teridentity appears or is needed as against one in which it seems | |
| − | + | not to be needed -- since assertion of identity can be made for any number | |
| − | + | of terms in the standard predicate calculus. | |
| − | + | ||
| − | + | This sort of statement totally non-plusses me. | |
| − | + | It seems like a complete non-sequitur or even | |
| − | + | a contradiction in terms to me. | |
| − | + | ||
| − | + | The question is about the minimal adequate resource base for | |
| − | + | defining, deriving, or generating all of the concepts that we | |
| − | + | need for a given but very general type of application that we | |
| − | + | conventionally but equivocally refer to as "logic". You seem | |
| − | + | to be saying something like this: We don't need 3-identity | |
| − | + | because we have 4-identity, 5-identity, 6-identity, ..., in | |
| − | + | the "standard predicate calculus". The question is not what | |
| − | + | concepts are generated in all the generations that follow the | |
| − | + | establishment of the conceptual resource base (axiom system), | |
| − | + | but what is the minimal set of concepts that we can use to | |
| − | + | generate the needed collection of concepts. And there the | |
| − | + | answer is, in a way that is subject to the usual sorts of | |
| − | + | mathematical proof, that 3-identity is the minimum while | |
| − | + | 2-identity is not big enough to do the job we want to do. | |
| − | + | ||
| − | + | Logic Of Relatives 01-41, LOR Discussion Notes 10-17. | |
| − | + | </pre> | |
| − | + | ||
| − | + | ===Discussion Note 18=== | |
| − | + | ||
| − | + | ; Jon Awbrey | |
| − | + | : but now I have to add to my do-list the problems of comparing the whole variorum of letters and drafts of letters to Lady Welby. I only have the CP 8 and Wiener versions here, so I will depend on you for ample excerpts from the Lieb volume. | |
| − | + | ||
| − | + | ; Bernard Morand | |
| − | ( | + | : I made such a kind of comparison some time ago. I selected the following 3 cases on the criterion of alternate "grounds". Hoping it could save some labor. The first rank expressions come from the MS 339 written in Oct. 1904 and I label them with an (a). I think that it is interesting to note that they were written four years before the letters to Welby and just one or two years after the Syllabus which is the usual reference for the classification in 3 trichotomies and 10 classes. The second (b) is our initial table (from a draft to Lady Welby, Dec. 1908, CP 8.344) and the third (c) comes from a letter sent in Dec. 1908 (CP 8.345–376). A tabular presentation would be better but I can't do it. Comparing (c) against (a) and (b) is informative, I think. |
| − | + | ||
| − | ( | + | ; Jon Awbrey |
| − | + | : Is this anywhere that it can be linked to from Arisbe? I've seen many pretty pictures of these things over the years, but may have to follow my own gnosis for a while. | |
| − | + | ||
| − | + | : Pages I have bookmarked just recently, but not really had the chance to study: | |
| − | + | ||
| − | + | : http://www.digitalpeirce.org/hoffmann/p-sighof.htm | |
| − | + | : http://www.csd.uwo.ca/~merkle/thesis/Introduction.html | |
| − | + | : http://members.door.net/arisbe/menu/library/aboutcsp/merkle/hci-abstract.htm | |
| − | ( | + | |
| − | + | ===Discussion Note 19=== | |
| − | ( | + | |
| − | + | <pre> | |
| − | + | BM = Bernard Morand | |
| − | + | JA = Jon Awbrey | |
| − | ( | + | |
| − | + | I now have three partially answered messages on the table, | |
| − | + | so I will just grab this fragment off the top of the deck. | |
| − | + | ||
| − | + | BM: Peirce gives the following definition (CP 8.343): | |
| − | + | ||
| − | + | BM, quoting CSP: | |
| − | + | ||
| − | + | | It is likewise requisite to distinguish | |
| − | + | | the 'Immediate Interpretant', i.e. the | |
| − | + | | Interpretant represented or signified in | |
| − | + | | the Sign, from the 'Dynamic Interpretant', | |
| − | + | | or effect actually produced on the mind | |
| − | + | | by the Sign; and both of these from | |
| − | + | | the 'Normal Interpretant', or effect | |
| − | + | | that would be produced on the mind by | |
| − | + | | the Sign after sufficient development | |
| − | + | | of thought. | |
| − | + | | | |
| − | + | | C.S. Peirce, 'Collected Papers', CP 8.343. | |
| − | + | ||
| − | + | JA: Well, you've really tossed me in the middle of the briar patch now! | |
| − | + | I must continue with my reading from the 1870 LOR, ... | |
| − | + | ||
| − | + | BM: Yes indeed! I am irritated by having not the necessary | |
| − | + | turn of mind to fully grasp it. But it seems to be a | |
| − | + | prerequisite in order to understand the very meaning | |
| − | + | of the above table. It could be the same for: | |
| − | + | ||
| − | + | BM, quoting CSP: | |
| − | + | ||
| − | + | | I define a 'Sign' as anything which on the one hand | |
| − | + | | is so determined by an Object and on the other hand | |
| − | + | | so determines an idea in a person's mind, that this | |
| − | + | | latter determination, which I term the 'Interpretant' | |
| − | + | | of the sign, is thereby mediately determined by that | |
| − | + | | Object. | |
| − | + | ||
| − | + | BM: The so-called "latter determination" would make the 'Interpretant' | |
| − | + | a tri-relative term into a teridentity involving Sign and Object. | |
| − | + | Isn't it? | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | BM: I thought previously that the Peirce's phrasing was just applying the | |
| + | principle of transitivity. From O determines S and S determines I, | ||
| + | it follows: O determines I. But this is not the same as teridentity. | ||
| + | Do you think so or otherwise? | ||
| − | + | My answers are "No" and "Otherwise". | |
| − | + | Continuing to discourse about definite universes thereof, | |
| − | + | the 3-identity term over the universe 1 = {A, B, C, D, ...} -- | |
| − | + | I only said it was definite, I didn't say it wasn't vague! -- | |
| − | + | designates, roughly speaking, the 3-adic relation that may | |
| − | + | be hinted at by way of the following series: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1,, = A:A:A +, B:B:B +, C:C:C +, D:D:D +, ... | |
| − | + | I did a study on Peirce's notion of "determination". | |
| − | + | As I understand it so far, we need to keep in mind | |
| − | + | that it is more fundamental than causation, can be | |
| − | + | a form of "partial determination", and is roughly | |
| − | + | formal, mathematical, or "information-theoretic", | |
| − | + | not of necessity invoking any temporal order. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | For example, when we say "The points A and B determine the line AB", | |
| − | + | this invokes the concept of a 3-adic relation of determination that | |
| − | + | does not identify A, B, AB, is not transitive, as transitivity has | |
| + | to do with the composition of 2-adic relations and would amount to | ||
| + | the consideration of a degenerate 3-adic relation in this context. | ||
| − | + | Now, it is possible to have a sign relation q whose sum enlists | |
| − | + | an elementary sign relation O:S:I where O = S = I. For example, | |
| − | + | it makes perfect sense to me to say that the whole universe may | |
| − | + | be a sign of itself to itself, so the conception is admissable. | |
| − | + | But this amounts to a very special case, by no means general. | |
| − | + | More generally, we are contemplating sums like the following: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | q = O1:S1:I1 +, O2:S2:I2 +, O3:S3:I3 +, ... |
| + | </pre> | ||
| − | + | ===Discussion Note 20=== | |
| − | + | ; Howard Callaway | |
| + | : Though I certainly hesitate to think that we are separated from the world by a veil of signs, it seems clear, too, on Peircean grounds, that no sign can ever capture its object completely. | ||
| − | + | ; Joe Ransdell | |
| − | + | : Any case of self-representation is a case of sign-object identity, in some sense of “identity”. I have argued in various places that this is the key to the doctrine of immediate perception as it occurs in Peirce's theory. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ; Jon Awbrey | |
| + | : To put the phrase back on the lathe: | ||
| − | + | : We are not separated from the world by a veil of signs — | |
| + | : we are the veil of signs. | ||
| − | + | ===Discussion Note 21=== | |
| − | + | <pre> | |
| − | + | AS = Armando Sercovich | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | AS: We are not separated from the world by a veil of signs nor we are a veil of signs. | |
| + | Simply we are signs. | ||
| − | + | AS, quoting CSP: | |
| − | + | | The *man-sign* acquires information, and comes to mean more than he did before. | |
| − | + | | But so do words. Does not electricity mean more now than it did in the days | |
| − | + | | of Franklin? Man makes the word, and the word means nothing which the man | |
| − | + | | has not made it mean, and that only to some man. But since man can think | |
| − | + | | only by means of words or other external symbols, these might turn round | |
| − | | | + | | and say: "You mean nothing which we have not taught you, and then only |
| − | + | | so far as you address some word as the interpretant of your thought". | |
| − | + | | In fact, therefore, men and words reciprocally educate each other; | |
| − | & | + | | each increase of a man's information involves, and is involved by, |
| − | + | | a corresponding increase of a word's information. | |
| − | + | | | |
| − | + | | Without fatiguing the reader by stretching this parallelism too far, it is | |
| − | + | | sufficient to say that there is no element whatever of man's consciousness | |
| − | + | | which has not something corresponding to it in the word; and the reason is | |
| + | | obvious. It is that the word or sign which man uses *is* the man itself. | ||
| + | | For, as the fact that every thought is a sign, taken in conjunction with | ||
| + | | the fact that life is a train of thought, proves that man is a sign; so, | ||
| + | | that every thought is an *external* sign proves that man is an external | ||
| + | | sign. That is to say, the man and the external sign are identical, in | ||
| + | | the same sense in which the words 'homo' and 'man' are identical. Thus | ||
| + | | my language is the sum total of myself; for the man is the thought ... | ||
| + | | | ||
| + | |'Charles S. Peirce: Selected Writings (Values in a Universe of Chance)', | ||
| + | | edited with an introduction and notes by Philip P. Wiener, Dover, | ||
| + | | New York, NY, 1966. Originally published under the subtitle | ||
| + | | in parentheses above, Doubleday & Company, 1958. | ||
| − | + | I read you loud and clear. | |
| + | Every manifold must have | ||
| + | its catalytic converter. | ||
| − | + | <Innumerate Continuation:> | |
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | TUC = The Usual CISPEC | |
| − | + | TUC Alert: | |
| − | + | | E.P.A. Says Catalytic Converter Is | |
| − | | | + | | Growing Cause of Global Warming |
| − | | | + | | By Matthew L. Wald |
| − | + | | Copyright 1998 The New York Times | |
| − | + | | May 29, 1998 | |
| + | | ----------------------------------------------------------------------- | ||
| + | | WASHINGTON -- The catalytic converter, an invention that has sharply | ||
| + | | reduced smog from cars, has now become a significant and growing cause | ||
| + | | of global warming, according to the Environmental Protection Agency | ||
| − | + | Much as I would like to speculate ad libitum on these exciting new prospects for the | |
| − | + | application of Peirce's chemico-algebraic theory of logic to the theorem-o-dynamics | |
| − | + | of auto-semeiosis, I must get back to "business as usual" (BAU) ... | |
| − | + | And now a word from our sponsor ... | |
| − | + | http://www2.naias.com/ | |
| − | + | Reporting from Motown --- | |
| − | + | Jon Awbrey | |
| + | </pre> | ||
| − | + | ===Discussion Note 22=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <pre> | |
| + | HC = Howard Callaway | ||
| − | + | HC: You quote the following passage from a prior posting of mine: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | HC: What remains relatively unclear is why we should need a system of notation | |
| + | in which teridentity appears or is needed as against one in which it seems | ||
| + | not to be needed -- since assertion of identity can be made for any number | ||
| + | of terms in the standard predicate calculus. | ||
| − | + | HC: You comment as follows: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | JA: This sort of statement totally non-plusses me. | |
| + | It seems like a complete non-sequitur or even | ||
| + | a contradiction in terms to me. | ||
| − | + | JA: The question is about the minimal adequate resource base for | |
| − | + | defining, deriving, or generating all of the concepts that we | |
| − | + | need for a given but very general type of application that we | |
| − | + | conventionally but equivocally refer to as "logic". You seem | |
| − | + | to be saying something like this: We don't need 3-identity | |
| − | + | because we have 4-identity, 5-identity, 6-identity, ..., in | |
| − | + | the "standard predicate calculus". The question is not what | |
| − | + | concepts are generated in all the generations that follow the | |
| − | + | establishment of the conceptual resource base (axiom system), | |
| − | + | but what is the minimal set of concepts that we can use to | |
| − | + | generate the needed collection of concepts. And there the | |
| − | + | answer is, in a way that is subject to the usual sorts of | |
| − | + | mathematical proof, that 3-identity is the minimum while | |
| + | 2-identity is not big enough to do the job we want to do. | ||
| − | + | HC: I have fallen a bit behind on this thread while attending to some other | |
| + | matters, but in this reply, you do seem to me to be coming around to an | ||
| + | understanding of the issues involved, as I see them. You put the matter | ||
| + | this way, "We don't need 3-identity because we have 4-identity, 5-identity, | ||
| + | 6-identity, ..., in the 'standard predicate calculus'". Actually, as I think | ||
| + | you must know, there is no such thing as "4-identity", "5-identity", etc., in | ||
| + | the standard predicate calculus. It is more that such concepts are not needed, | ||
| + | just as teridentity is not needed, since the general apparatus of the predicate | ||
| + | calculus allows us to express identity among any number of terms without special | ||
| + | provision beyond "=". | ||
| − | + | No, that is not the case. Standard predicate calculus allows the expression | |
| − | + | of predicates I_k, for k = 2, 3, 4, ..., such that I_k (x_1, ..., x_k) holds | |
| − | + | if and only if all x_j, for j = 1 to k, are identical. So predicate calculus | |
| − | + | contains a k-identity predicate for all such k. So whether "they're in there" | |
| − | + | is not an issue. The question is whether these or any other predicates can be | |
| − | + | constructed or defined in terms of 2-adic relations alone. And the answer is | |
| − | + | no, they cannot. The vector of the misconception counterwise appears to be | |
| − | + | as various a virus as the common cold, and every bit as resistant to cure. | |
| − | + | I have taken the trouble to enumerate some of the more prevalent strains, | |
| − | + | but most of them appear to go back to the 'Principia Mathematica', and | |
| − | + | the variety of nominalism called "syntacticism" -- Ges-und-heit! -- | |
| − | + | that was spread by it, however unwittedly by some of its carriers. | |
| − | + | </pre> | |
| − | |||
| − | |||
| − | |||
| − | + | ===Discussion Note 23=== | |
| − | + | ; Jon Awbrey | |
| − | + | : In trying to answer the rest of your last note, it seems that we cannot go any further without achieving some concrete clarity as to what is denominated by “standard predicate calculus”, that is, “first order logic”, or whatever. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | I | + | : There is a canonical presentation of the subject, as I remember it, anyway, in the following sample of materials from Chang and Keisler's <i>Model Theory</i>. (There's a newer edition of the book but this part of the subject hasn't really changed all that much in ages.) |
| − | + | : Model Theory 01-39 | |
| − | + | ===Discussion Note 24=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <pre> | |
| + | HC = Howard Callaway | ||
| − | + | HC: I might object that "teridentity" seems to come | |
| − | + | to a matter of "a=b & b=c", so that a specific | |
| − | + | predicate of teridentity seems unnecessary. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | I am presently concerned with expositing and interpreting | |
| − | + | the logical system that Peirce laid out in the LOR of 1870. | |
| − | + | It is my considered opinion after thirty years of study that | |
| + | there are untapped resources remaining in this work that have | ||
| + | yet to make it through the filters of that ilk of syntacticism | ||
| + | that was all the rage in the late great 1900's. I find there | ||
| + | to be an appreciably different point of view on logic that is | ||
| + | embodied in Peirce's work, and until we have made the minimal | ||
| + | effort to read what he wrote it is just plain futile to keep | ||
| + | on pretending that we have already assimilated it, or that | ||
| + | we are qualified to evaluate its cogency. | ||
| − | + | The symbol "&" that you employ above denotes a mathematical object that | |
| + | qualifies as a 3-adic relation. Independently of my own views, there | ||
| + | is an abundance of statements in evidence that mathematical thinkers | ||
| + | from Peirce to Goedel consider the appreciation of facts like this | ||
| + | to mark the boundary between realism and nominalism in regard to | ||
| + | mathematical objects. | ||
| + | </pre> | ||
| − | + | ===Discussion Note 25=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <pre> | |
| + | HC = Howard Callaway | ||
| + | JA = Jon Awbrey | ||
| − | + | HC: I might object that "teridentity" seems to come | |
| + | to a matter of "a=b & b=c", so that a specific | ||
| + | predicate of teridentity seems unnecessary. | ||
| − | + | JA: I am presently concerned with expositing and interpreting | |
| + | the logical system that Peirce laid out in the LOR of 1870. | ||
| + | It is my considered opinion after thirty years of study that | ||
| + | there are untapped resources remaining in this work that have | ||
| + | yet to make it through the filters of that ilk of syntacticism | ||
| + | that was all the rage in the late great 1900's. I find there | ||
| + | to be an appreciably different point of view on logic that is | ||
| + | embodied in Peirce's work, and until we have made the minimal | ||
| + | effort to read what he wrote it is just plain futile to keep | ||
| + | on pretending that we have already assimilated it, or that | ||
| + | we are qualified to evaluate its cogency. | ||
| − | + | JA: The symbol "&" that you employ above denotes a mathematical object that | |
| + | qualifies as a 3-adic relation. Independently of my own views, there | ||
| + | is an abundance of statements in evidence that mathematical thinkers | ||
| + | from Peirce to Goedel consider the appreciation of facts like this | ||
| + | to mark the boundary between realism and nominalism in regard to | ||
| + | mathematical objects. | ||
| − | + | HC: I would agree, I think, that "&" may be thought of | |
| + | as a function mapping pairs of statements onto the | ||
| + | conjunction of that pair. | ||
| − | + | Yes, indeed, in the immortal words of my very first college algebra book: | |
| − | + | "A binary operation is a ternary relation". As it happens, the symbol "&" | |
| − | + | is equivocal in its interpretation -- computerese today steals a Freudian | |
| − | + | line and dubs it "polymorphous" -- it can be regarded in various contexts | |
| − | + | as a 3-adic relation on syntactic elements called "sentences", on logical | |
| − | + | elements called "propositions", or on truth values collated in the boolean | |
| − | + | domain B = {false, true} = {0, 1}. But the mappings and relations between | |
| − | + | all of these interpretive choices are moderately well understood. Still, | |
| − | + | no matter how many ways you enumerate for looking at a B-bird, the "&" is | |
| − | + | always 3-adic. And that is sufficient to meet your objection, so I think | |
| − | + | I will just leave it there until next time. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | On a related note, that I must postpone until later: | |
| − | + | We seem to congrue that there is a skewness between | |
| − | + | the way that most mathematicians use logic and some | |
| − | + | philosophers talk about logic, but I may not be the | |
| − | + | one to set it adjoint, much as I am inclined to try. | |
| − | + | At the moment I have this long-post-poned exponency | |
| − | + | to carry out. I will simply recommend for your due | |
| − | + | consideration Peirce's 1870 Logic Of Relatives, and | |
| − | + | leave it at that. There's a cornucopiousness to it | |
| − | + | that's yet to be dreamt of in the philosophy of the | |
| − | + | 1900's. I am doing what I can to infotain you with | |
| − | + | the Gardens of Mathematical Recreations that I find | |
| − | + | within Peirce's work, and that's in direct response | |
| − | + | to many, okay, a couple of requests. Perhaps I can | |
| − | + | not hope to attain the degree of horticultural arts | |
| − | + | that Gardners before me have exhibited in this work, | |
| − | + | but then again, who could? Everybody's a critic -- | |
| − | + | but the better ones read first, and criticize later. | |
| − | + | </pre> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Discussion Note 26=== | |
| − | + | ; Howard Callaway | |
| − | + | : But on the other hand, it is not customary to think of “&” as a relation among statements or sentences — as, for instance, logical implication is considered a logical relation between statements or sentences. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ; Jon Awbrey | |
| + | : Actually, it is the custom in many quarters to treat all of the boolean operations, logical connectives, propositional relations, or whatever you want to call them, as “equal citizens”, having each their “functional” (f : B^k -> B) and their “relational” (L c B^(k+1)) interpretations and applications. From this vantage, the interpretive distinction that is commonly regarded as that between “assertion” and mere “contemplation” is tantamount to a “pragmatic” difference between computing the values of a function on a given domain of arguments and computing the inverse of a function vis-a-vis a prospective true value. This is the logical analogue of the way that our mathematical models of reality have long been working, unsuspected and undisturbed by most philosophers of science, I might add. If only the logical side of the ledger were to be developed rather more fully than it is at present, we might wake one of these days to find our logical accounts of reality, finally, at long last, after an overweaningly longish adolescence, beginning to come of age. | ||
| − | + | ===Discussion Note 27=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <pre> | |
| + | HC = Howard Callaway | ||
| − | + | HC: For, if I make an assertion A&B, then I am not asserting | |
| − | + | that the statement A stands in a relation to a statement B. | |
| − | + | Instead, I am asserting the conjunction A&B (which logically | |
| − | + | implies both the conjuncts in view of the definition of "&"). | |
| − | |||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | & | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Please try to remember where we came in. This whole play of | |
| − | + | animadversions about 3-adicity and 3-identity is set against | |
| − | + | the backdrop of a single point, over the issue as to whether | |
| − | + | 3-adic relations are wholly dispensable or somehow essential | |
| − | + | to logic, mathematics, and indeed to argument, communication, | |
| + | and reasoning in general. Some folks clamor "Off with their | ||
| + | unnecessary heads!" -- other people, who are forced by their | ||
| + | occupations to pay close attention to the ongoing complexity | ||
| + | of the processes at stake, know that, far from finding 3-ads | ||
| + | in this or that isolated corner of the realm, one can hardly | ||
| + | do anything at all in the ways of logging or mathing without | ||
| + | running smack dab into veritable hosts of them. | ||
| − | + | I have just shown that "a=b & b=c" involves a 3-adic relation. | |
| − | + | Some people would consider this particular 3-adic relation to | |
| − | + | be more complex than the 3-identity relation, but that may be | |
| − | + | a question of taste. At any rate, the 3-adic aspect persists. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | a | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | HC: If "&" counts as a triadic relation, simply because it serves | |
| + | to conjoin two statements into a third, then it would seem that | ||
| + | any binary relation 'R' will count as triadic, simply because | ||
| + | it places two things into a relation, which is a "third" thing. | ||
| + | By the same kind of reasoning a triadic relation, as ordinarily | ||
| + | understood would be really 4-adic. | ||
| − | + | The rest of your comments are just confused, | |
| + | and do not use the terms as they are defined. | ||
| + | </pre> | ||
| − | + | ===Discussion Note 28=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <pre> | |
| + | JA = Jon Awbrey | ||
| + | JR = Joseph Ransdell | ||
| − | + | JA: Notice that Peirce follows the mathematician's usual practice, | |
| + | then and now, of making the status of being an "individual" or | ||
| + | a "universal" relative to a discourse in progress. I have come | ||
| + | to appreciate more and more of late how radically different this | ||
| + | "patchwork" or "piecewise" approach to things is from the way of | ||
| + | some philosophers who seem to be content with nothing less than | ||
| + | many worlds domination, which means that they are never content | ||
| + | and rarely get started toward the solution of any real problem. | ||
| + | Just my observation, I hope you understand. | ||
| − | + | JR: Yes, I take this as underscoring and explicating the import of | |
| + | making logic prior to rather than dependent upon metaphysics. | ||
| − | + | I think that Peirce, and of course many math folks, would take math | |
| − | + | as prior, on a par, or even identical with logic. Myself I've been | |
| − | + | of many minds about this over the years. The succinctest picture | |
| − | + | that I get from Peirce is always this one: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | | [Riddle of the Sphynx] | |
| + | | | ||
| + | | Normative science rests largely on phenomenology and on mathematics; | ||
| + | | Metaphysics on phenomenology and on normative science. | ||
| + | | | ||
| + | | C.S. Peirce, CP 1.186 (1903) | ||
| + | | | ||
| + | | | ||
| + | | o Metaphysics | ||
| + | | /| | ||
| + | | / | | ||
| + | | / | | ||
| + | | Normative Science o | | ||
| + | | / \ | | ||
| + | | / \ | | ||
| + | | / \| | ||
| + | | Mathematics o o Phenomenology | ||
| + | | | ||
| + | | | ||
| + | | ROTS. http://stderr.org/pipermail/inquiry/2004-March/001262.html | ||
| − | + | Logic being a normative science must depend on math and phenomenology. | |
| − | + | Of course, it all depends on what a person means by "logic" ... | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | JA: I also observe that Peirce takes the individual objects of | |
| + | a particular universe of discourse in a "generative" way, | ||
| + | not a "totalizing" way, and thus they afford us with the | ||
| + | basis for talking freely about collections, constructions, | ||
| + | properties, qualities, subsets, and "higher types", as | ||
| + | the phrase is mint. | ||
| − | + | JR: Would this be essentially the same as regarding quantification as | |
| + | distributive rather than collective, i.e. we take the individuals | ||
| + | of a class one-by-one as selectable rather than as somehow given | ||
| + | all at once, collectively? | ||
| − | + | Gosh, that's a harder question. Your suggestion reminds me | |
| − | + | of the way that some intuitionist and even some finitist | |
| − | + | mathematicians talk when they reflect on math practice. | |
| − | + | I have leanings that way, but when I have tried to | |
| − | + | give up the classical logic axioms, I have found | |
| − | + | them too built in to my way of thinking to quit. | |
| − | + | Still, a healthy circumspection about about our | |
| − | + | often-wrongly vaunted capacties to conceive of | |
| − | + | totalities is a habitual part of current math. | |
| + | Again, I think individuals are made not born, | ||
| + | that is, to some degree factitious and mere | ||
| + | compromises of this or that conveniency. | ||
| + | This is one of the reasons that I have | ||
| + | been trying to work out the details | ||
| + | of a functional approach to logic, | ||
| + | propostional, quantificational, | ||
| + | and relational. | ||
| + | |||
| + | Cf: INTRO 30. http://stderr.org/pipermail/inquiry/2004-November/001765.html | ||
| + | In: INTRO. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1720 | ||
| + | </pre> | ||
| − | + | ===Discussion Note 29=== | |
| − | + | <pre> | |
| − | + | JA = Jon Awbrey | |
| − | < | + | GR = Gary Richmond |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Re: LOR.COM 11.24. http://stderr.org/pipermail/inquiry/2004-November/001836.html | |
| + | In: LOR.COM. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1755 | ||
| − | + | JA: The manner in which these arrows and qualified arrows help us | |
| − | + | to construct a suspension bridge that unifies logic, semiotics, | |
| − | + | statistics, stochastics, and information theory will be one of | |
| − | + | the main themes that I aim to elaborate throughout the rest of | |
| − | + | this inquiry. | |
| − | + | ||
| − | + | GR: Pretty ambitious, Jon. I'm sure you're up to it. | |
| − | + | ||
| − | + | GR: I'd like to anticipate 3 versions: The mathematical (cactus diagrams, etc.), | |
| − | + | the poetic, and the commonsensical -- ordinary language for those who are | |
| − | + | NEITHER logicians NOR poets. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | GR: Are you up to THAT? | |
| − | + | Riddle A Body: "Time Enough, And Space, Excalibrate Co-Arthurs Should Apply" | |
| − | + | </pre> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Discussion Note 30=== | |
| − | + | <pre> | |
| + | JA = Jon Awbrey | ||
| + | GR = Gary Richmond | ||
| − | + | Re: LOR.DIS 29. http://stderr.org/pipermail/inquiry/2004-November/001838.html | |
| + | In: LOR.DIS. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768 | ||
| − | + | JA: Riddle A Body: "Time Enough, And Space, Excalibrate Co-Arthurs Should Apply" | |
| − | + | GR: Well said, and truly! | |
| − | + | Body A Riddle: TEASE CASA = Fun House. | |
| − | + | </pre> | |
| − | + | ||
| − | + | ===Discussion Note 31=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Many illusions of selective reading — like the myth that Peirce did not discover quantification over indices until 1885 — can be dispelled by looking into his 1870 “Logic of Relatives”. I started a web study of this in 2002, reworked again in 2003 and 2004, the current version of which can be found here: | |
| − | + | * [http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1750 LOR Selections] | |
| + | * [http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1755 LOR Comments] | ||
| + | * [http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768 LOR Discussion] | ||
| − | + | I've only gotten as far as the bare infrastructure of Peirce's 1870 LOR, but an interesting feature of the study is that, if one draws the pictures that seem almost demanded by his way of linking up indices over expressions, then one can see a prototype of his much later logical graphs developing in the text. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Discussion Work Areas== | |
| − | + | ===Discussion Work Area 1=== | |
| − | + | <pre> | |
| − | + | BM: Several discussions could take place there, | |
| − | + | as to the reasons for the number of divisions, | |
| − | + | the reasons of the titles themselves. Another | |
| − | + | one is my translation from "normal interpretant" | |
| − | + | into "final interpretant" (which one is called | |
| − | + | elsewhere "Eventual Interpretant" or "Destinate | |
| − | + | Interpretant" by CSP). I let all this aside | |
| − | + | to focus on the following remark: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | BM: 6 divisions correspond to individual correlates: | |
| − | + | (S, O_i, O_d, I_i, I_d, I_n), | |
| − | + | 3 divisions correspond to dyads: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (S : O_d, S : I_d, S : I_n), | |
| − | + | and the tenth to a triad: | |
| − | + | (S : O_d : I_n). | |
| − | + | This remark would itself deserve | |
| + | a lot of explanations but one | ||
| + | more time I let this aside. | ||
| − | + | BM: Then we have the following very clear statement from Peirce: | |
| − | + | | It follows from the Definition of a Sign | |
| + | | that since the Dynamoid Object determines | ||
| + | | the Immediate Object, | ||
| + | | which determines the Sign, | ||
| + | | which determines the Destinate Interpretant | ||
| + | | which determines the Effective Interpretant | ||
| + | | which determines the Explicit Interpretant | ||
| + | | | ||
| + | | the six trichotomies, instead of determining 729 classes of signs, | ||
| + | | as they would if they were independent, only yield 28 classes; and | ||
| + | | if, as I strongly opine (not to say almost prove) there are four other | ||
| + | | trichotomies of signs of the same order of importance, instead of making | ||
| + | | 59049 classes, these will only come to 66. | ||
| + | | | ||
| + | | CSP, "Letter to Lady Welby", 14 Dec 1908, LW, p. 84. | ||
| − | + | BM: The separation made by CSP between 6 divisions and four others | |
| + | seems to rely upon the suggested difference between individual | ||
| + | correlates and relations. We get the idea that the 10 divisions | ||
| + | are ordered on the whole and will end into 66 classes (by means of | ||
| + | three ordered modal values on each division: maybe, canbe, wouldbe). | ||
| + | Finally we have too the ordering for the divisions relative to the | ||
| + | correlates that I write in my notation: | ||
| − | + | Od -> Oi -> S -> If -> Id -> Ii. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | BM: This order of "determinations" has bothered many people | |
| − | + | but if we think of it as operative in semiosis, it seems | |
| − | + | to be correct (at least to my eyes). Thus the question is: | |
| − | + | where, how, and why the "four other trichotomies" fit in this | |
| − | + | schema to obtain a linear ordering on the whole 10 divisions? | |
| − | + | May be the question can be rephrased as: how intensional | |
| − | + | relationships fit into an extensional one? Possibly the | |
| − | + | question could be asked the other way. R. Marty responds | |
| − | + | that in a certain sense the four trichotomies give nothing | |
| − | + | more than the previous six ones but I strongly doubt of this. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | BM: I put the problem in graphical form in an attached file | |
| + | because my message editor will probably make some mistakes. | ||
| + | I make a distinction between arrow types drawing because I am | ||
| + | not sure that the sequence of correlates determinations is of | ||
| + | the same nature than correlates determination inside relations. | ||
| − | + | BM: It looks as if the problem amounts to some kind of projection | |
| + | of relations on the horizontal axis made of correlates. | ||
| − | + | BM: If we consider some kind of equivalence (and this seems necessary to | |
| − | + | obtain a linear ordering), by means of Agent -> Patient reductions on | |
| − | + | relations, then erasing transitive determinations leads to: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Od -> Oi -> S -> S-Od -> If -> S-If -> S-Od-If -> Id -> S-Id -> Ii | |
| − | + | BM: While it is interesting to compare the subsequence | |
| − | + | S-Od -> If -> S-If -> S-Od-If with the pragmatic maxim, | |
| − | + | I have no clear idea of the (in-) validity of such a result. | |
| + | But I am convinced that the clarity has to come from the | ||
| + | Logic Of Relatives. | ||
| − | + | BM: I will be very grateful if you can make something with all that stuff. | |
| + | </pre> | ||
| − | + | ===Discussion Work Area 2=== | |
| − | + | <pre> | |
| − | + | BM: I also found this passage which may be of some interest | |
| − | + | (CP 4.540, Prolegomena to an Apology of Pragmatism): | |
| − | |||
| − | |||
| − | + | | But though an Interpretant is not necessarily a Conclusion, yet a | |
| + | | Conclusion is necessarily an Interpretant. So that if an Interpretant is | ||
| + | | not subject to the rules of Conclusions there is nothing monstrous in my | ||
| + | | thinking it is subject to some generalization of such rules. For any | ||
| + | | evolution of thought, whether it leads to a Conclusion or not, there is a | ||
| + | | certain normal course, which is to be determined by considerations not in | ||
| + | | the least psychological, and which I wish to expound in my next | ||
| + | | article;†1 and while I entirely agree, in opposition to distinguished | ||
| + | | logicians, that normality can be no criterion for what I call | ||
| + | | rationalistic reasoning, such as alone is admissible in science, yet it | ||
| + | | is precisely the criterion of instinctive or common-sense reasoning, | ||
| + | | which, within its own field, is much more trustworthy than rationalistic | ||
| + | | reasoning. In my opinion, it is self-control which makes any other than | ||
| + | | the normal course of thought possible, just as nothing else makes any | ||
| + | | other than the normal course of action possible; and just as it is | ||
| + | | precisely that that gives room for an ought-to-be of conduct, I mean | ||
| + | | Morality, so it equally gives room for an ought-to-be of thought, which | ||
| + | | is Right Reason; and where there is no self-control, nothing but the | ||
| + | | normal is possible. If your reflections have led you to a different | ||
| + | | conclusion from mine, I can still hope that when you come to read my next | ||
| + | | article, in which I shall endeavor to show what the forms of thought are, | ||
| + | | in general and in some detail, you may yet find that I have not missed | ||
| + | | the truth. | ||
| − | + | JA: Just as I have always feared, this classification mania | |
| − | + | appears to be communicable! But now I must definitely | |
| − | + | review the Welby correspondence, as all this stuff was | |
| − | + | a blur to my sensibilities the last 10 times I read it. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | BM: I think that I understand your reticence. I wonder if: | |
| − | + | a. the fact that the letters to Lady Welby have been published as such, | |
| + | has not lead to approach the matter in a certain way. | ||
| − | + | b. other sources, eventually unpublished, would give another lighting on | |
| − | + | the subject, namely a logical one. I think of MS 339 for example that | |
| − | + | seems to be part of the Logic Notebook. I have had access to some pages | |
| − | + | of it, but not to the whole MS. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | A | + | BM: A last remark. I don't think that classification is a mania for CSP but I |
| + | know that you know that! It is an instrument of thought and I think that | ||
| + | it is in this case much more a plan for experimenting than the exposition | ||
| + | of a conclusion. Experimenting what ? There is a strange statement in a | ||
| + | letter to W. James where CSP says that what is in question in his "second | ||
| + | way of dividing signs" is the logical theory of numbers. I give this from | ||
| + | memory. I have not the quote at hand now but I will search for it if needed. | ||
| + | </pre> | ||
| − | + | ===Discussion Work Area 3=== | |
| − | + | <pre> | |
| − | + | BM = Bernard Morand | |
| − | + | JA = Jon Awbrey | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | JA: ... but now I have to add to my do-list the problems of comparing | |
| + | the whole variorum of letters and drafts of letters to Lady Welby. | ||
| + | I only have the CP 8 and Wiener versions here, so I will depend | ||
| + | on you for ample excerpts from the Lieb volume. | ||
| − | + | BM: I made such a kind of comparison some time ago. I selected the following | |
| + | 3 cases on the criterium of alternate "grounds". Hoping it could save | ||
| + | some labor. The first rank expressions come from the MS 339 written in | ||
| + | Oct. 1904 and I label them with an (a). I think that it is interesting to | ||
| + | note that they were written four years before the letters to Welby and | ||
| + | just one or two years after the Syllabus which is the usual reference for | ||
| + | the classification in 3 trichotomies and 10 classes. The second (b) is | ||
| + | our initial table (from a draft to Lady Welby, Dec. 1908, CP 8.344) and | ||
| + | the third (c) comes from a letter sent in Dec. 1908 (CP 8.345-8.376). A | ||
| + | tabular presentation would be better but I can't do it. Comparing (c) | ||
| + | against (a) and (b) is informative, I think. | ||
| + | |||
| + | Division 1 | ||
| − | + | (a) According to the matter of the Sign | |
| − | + | (b) According to the Mode of Apprehension of the Sign itself | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (c) Signs in respect to their Modes of possible Presentation | |
| − | + | Division 2 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (a) According to the Immediate Object | |
| − | + | (b) According to the Mode of Presentation of the Immediate Object | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (c) Objects, as they may be presented | |
| − | + | Division 3 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (a) According to the Matter of the Dynamic Object | |
| − | + | (b) According to the Mode of Being of the Dynamical Object | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (c) In respect to the Nature of the Dynamical Objects of Signs | |
| − | + | Division 4 | |
| − | + | (a) According to the mode of representing object by the Dynamic Object | |
| − | + | (b) According to the Relation of the Sign to its Dynamical Object | |
| − | + | (c) The fourth Trichotomy | |
| − | + | Division 5 | |
| − | + | (a) According to the Immédiate Interpretant | |
| − | |||
| − | |||
| − | + | (b) According to the Mode of Presentation of the Immediate Interpretant | |
| − | + | (c) As to the nature of the Immediate (or Felt ?) Interpretant | |
| − | + | Division 6 | |
| − | + | (a) According to the Matter of Dynamic Interpretant | |
| − | + | (b) According to the Mode of Being of the Dynamical Interpretant | |
| − | + | (c) As to the Nature of the Dynamical Interpretant | |
| − | + | Division 7 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (a) According to the Mode of Affecting Dynamic Interpretant | |
| − | + | (b) According to the relation of the Sign to the Dynamical Interpretant | |
| − | + | (c) As to the Manner of Appeal to the Dynamic Interpretant | |
| − | + | Division 8 | |
| − | + | (a) According to the Matter of Representative Interpretant | |
| − | + | (b) According to the Nature of the Normal Interpretant | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (c) According to the Purpose of the Eventual Interpretant | |
| − | + | Division 9 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (a) According to the Mode of being represented by Representative Interpretant | |
| − | + | (b) According to the the relation of the Sign to the Normal Interpretant | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (c) As to the Nature of the Influence of the Sign | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Division 10 | |
| − | + | (a) According to the Mode of being represented to represent object by Sign, Truly | |
| − | + | (b) According to the Triadic Relation of the Sign to its Dynamical Object and to | |
| + | its Normal Interpretant | ||
| − | + | (c) As to the Nature of the Assurance of the Utterance | |
| + | </pre> | ||
| − | === | + | ===Discussion Work Area 4=== |
| − | |||
| − | |||
<pre> | <pre> | ||
| − | a | + | JA: It may appear that one has side-stepped the issue of empiricism |
| − | + | that way, but then all that stuff about the synthetic a priori | |
| − | + | raises its head, and we have Peirce's insight that mathematics | |
| − | + | is observational and even experimental, and so I must trail off | |
| − | + | into uncoordinated elliptical thoughts ... | |
| − | + | ||
| − | + | HC: In contrast with this it strikes me that not all meanings of "analytic" | |
| − | + | and "synthetic" have much, if anything, to do with the "analytic and the | |
| − | + | synthetic", say, as in Quine's criticism of the "dualism" of empiricism. | |
| − | + | Surely no one thinks that a plausible analysis must be analytic or that | |
| − | + | synthetic materials tell us much about epistemology. So, it is not | |
| + | clear that anything connected with analyticity or a priori knowledge | ||
| + | will plausibly or immediately arise from a discussion of analytical | ||
| + | geometry. Prevalent mathematical assumptions or postulates, yes -- | ||
| + | but who says these are a prior? Can't non-Euclidean geometry also | ||
| + | be treated in the style of analytic geometry? | ||
| + | |||
| + | HC: I can imagine the a discussion might be forced in | ||
| + | that direction, but the connections don't strike me | ||
| + | as at all obvious or pressing. Perhaps Jon would just | ||
| + | like to bring up the notion of the synthetic apriori? | ||
| + | But why? | ||
</pre> | </pre> | ||
| − | |||
| − | + | ===Discussion Work Area 5=== | |
| − | + | ||
<pre> | <pre> | ||
| − | + | HC = Howard Callaway | |
| − | + | ||
| − | + | HC: But I see you as closer to my theme or challenge, when you say | |
| − | + | "The question is about the minimal adequate resource base for | |
| − | + | defining, deriving, or generating all of the concepts that we | |
| − | + | need for a given but very general type of application that we | |
| − | + | conventinally but equivocally refer to as 'logic'". | |
| − | |||
| − | |||
| − | |||
| − | a | ||
| − | |||
| − | |||
| − | + | HC: I think it is accepted on all sides of the discussion that there | |
| + | is some sort of "equivalence" between the standard predicate logic | ||
| + | and Peirce's graphs. | ||
| − | + | There you would be mistaken, except perhaps for the fact that | |
| − | + | "some sort of equivalence" is vague to the depths of vacuity. | |
| − | + | It most particularly does not mean "all sorts of equivalence" | |
| − | a | + | or even "all important sorts of equivalence". It is usually |
| − | + | interpreted to mean an extremely abstract type of syntactic | |
| − | + | equivalence, and that is undoubtedly one important type of | |
| − | + | equivalence that it is worth examining whether two formal | |
| − | + | systems have or not. But it precisely here that we find | |
| − | + | another symptom of syntacticism, namely, the deprecation | |
| − | + | of all other important qualities of formal systems, most | |
| − | + | pointedly their "analystic, "semantic", and "pragmatic" | |
| − | + | qualities, which make all the difference in how well the | |
| − | + | system actually serves its users in a real world practice. | |
| − | + | You can almost hear the whining and poohing coming from the | |
| + | syntactic day camp, but those are the hard facts of the case. | ||
| + | |||
| + | HC: But we find this difference in relation to the vocabulary used to express | ||
| + | identity. From the point of view of starting with the predicate calculus, | ||
| + | we don't need "teridentity". So, this seems to suggest there is something | ||
| + | of interesting contrast in Peirce's logic, which brings in this concept. | ||
| + | The obvious question may be expressed by asking why we need teridentity | ||
| + | in Peirce's system and how Peirce's system may recommend itself in contrast | ||
| + | to the standard way with related concepts. This does seem to call for | ||
| + | a comparative evaluation of distinctive systems. That is not an easy task, | ||
| + | as I think we all understand. But I do think that if it is a goal to have | ||
| + | Peirce's system better appreciated, then that kind of question must be | ||
| + | addressed. If "=" is sufficient in the standard predicate calculus, | ||
| + | to say whatever we may need to say about the identity of terms, then | ||
| + | what is the advantage of an alternative system which insists on always | ||
| + | expressing identity of triples? | ||
| + | |||
| + | HC: The questions may look quite different, depending on where we start. | ||
| + | But in any case, I thought I saw some better appreciation of the | ||
| + | questions in your comments above. | ||
</pre> | </pre> | ||
| − | |||
| − | === | + | ===Discussion Work Area 6=== |
| − | + | <pre> | |
| − | + | ||
| − | < | + | It's been that way for about as long as anybody can remember, and |
| − | + | it will remain so, in spite of the spate of history rewriting and | |
| − | + | image re-engineering that has become the new rage in self-styled | |
| − | + | "analytic" circles. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
| − | |||
| − | + | ===Discussion Work Area 7=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<pre> | <pre> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The brands of objection that you continue to make, with no evidence | |
| − | + | of reflection on the many explanations that I and others have taken | |
| − | + | the time to write out for you, lead me to believe that you are just | |
| − | + | not interested in making that effort. That's okay, life is short, | |
| − | + | the arts are long and many, there is always something else to do. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | HC: For, if I make an assertion A&B, then I am not asserting | |
| + | that the statement A stands in a relation to a statement B. | ||
| + | Instead, I am asserting the conjunction A&B (which logically | ||
| + | implies both the conjuncts in view of the definition of "&"). | ||
| + | If "&" counts as a triadic relation, simply because it serves | ||
| + | to conjoin two statements into a third, then it would seem that | ||
| + | any binary relation 'R' will count as triadic, simply because | ||
| + | it places two things into a relation, which is a "third" thing. | ||
| + | By the same kind of reasoning a triadic relation, as ordinarily | ||
| + | understood would be really 4-adic. | ||
| − | + | HC: Now, I think this is the kind of argument you are making, ... | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | No, it's the kind of argument that you are making. | |
| − | + | I am not making that kind of argument, and Peirce | |
| − | + | did not make that kind of argument. Peirce used | |
| − | + | his terms subject to definitions that would have | |
| − | + | been understandable, and remain understandable, | |
| − | + | to those of his readers who understand these | |
| − | + | elementary definitions, either though their | |
| + | prior acquaintance with standard concepts | ||
| + | or through their basic capacity to read | ||
| + | a well-formed, if novel definition. | ||
| − | + | Peirce made certain observations about the structure of logical concepts | |
| − | + | and the structure of their referents. Those observations are accurate | |
| − | + | and important. He expressed those observations in a form that is clear | |
| − | + | to anybody who knows the meanings of the technical terms that he used, | |
| − | + | and he is not responsible for the interpretations of those who don't. | |
| − | |||
| − | + | HC: ... and it seems to both trivialize the claimed argument | |
| − | + | for teridentity, by trivializing the conception of what | |
| − | + | is to count as a triadic, as contrasted with a binary | |
| − | + | relation, and it also seems to introduce a confusion | |
| − | + | about what is is count as a binary, vs. a triadic | |
| − | + | relation. | |
| − | |||
| − | + | Yes, the argument that you are making trivializes | |
| − | + | just about everything in sight, but that is the | |
| − | + | common and well-known property of any argument | |
| − | + | that fails to base itself on a grasp of the | |
| − | + | first elements of the subject matter. | |
| − | |||
| − | |||
| − | + | HC: If this is mathematical realism, then so much the worse for | |
| − | + | mathematical realism. I am content to think that we do not | |
| − | + | have a free hand in making up mathematical truth. | |
| − | + | ||
| − | + | No, it's not mathematical realism. It is your reasoning, | |
| − | + | and it exhibits all of the symptoms of syntacticism that | |
| − | + | I have already diagnosed. It's a whole other culture | |
| + | from what is pandemic in the practice of mathematics, | ||
| + | and it never fails to surprise me that people who | ||
| + | would never call themselves "relativists" in any | ||
| + | other matter of culture suddenly turn into just | ||
| + | that in matters of simple mathematical fact. | ||
| − | + | </pre> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | + | ==Work Area== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Figure 51=== |
| − | + | ====Version 1==== | |
| − | {| align="center" cellspacing="6" width="90%" | + | {| align="center" cellspacing ="6" width="90%" |
| | | | ||
| − | < | + | <pre> |
| − | + | t_1 t_32 t_33 t_64 t_65 t_96 ... ... | |
| − | \ | + | o ... o o ... o o ... o o ... o U |
| − | \ | + | \ | / \ | / \ | / \ | / |
| − | \ | + | \ | / \ | / \ | / \ | / T |
| − | </ | + | \|/ \|/ \|/ \|/ |
| + | o o o o V | ||
| + | m_1 m_2 m_3 ... | ||
| + | </pre> | ||
|} | |} | ||
| − | + | ====Version 2==== | |
| − | |||
| − | |||
| − | {| align="center" cellspacing="6" width="90%" | + | {| align="center" cellspacing ="6" width="90%" |
| − | | < | + | | |
| + | <pre> | ||
| + | T_1 T_32 T_33 T_64 T_65 T_96 ... ... | ||
| + | o ... o o ... o o ... o o ... o t | ||
| + | \ | / \ | / \ | / \ | / | ||
| + | \ | / \ | / \ | / \ | / 't' | ||
| + | \|/ \|/ \|/ \|/ | ||
| + | o o o o m | ||
| + | M_1 M_2 M_3 ... | ||
| + | </pre> | ||
|} | |} | ||
| − | {| align="center" cellspacing="6" width="90%" | + | ====Version 3==== |
| − | | < | + | |
| + | {| align="center" cellspacing ="6" width="90%" | ||
| + | | | ||
| + | <pre> | ||
| + | M_1 M_2 M_3 ... | ||
| + | o o o o m | ||
| + | /|\ /|\ /|\ /|\ | ||
| + | / | \ / | \ / | \ / | \ 't' | ||
| + | / | \ / | \ / | \ / | \ | ||
| + | o ... o o ... o o ... o o ... o t | ||
| + | T_1 T_32 T_33 T_64 T_65 T_96 ... ... | ||
| + | </pre> | ||
|} | |} | ||
| − | + | ==Mathematical Demonstration and the Doctrine of Individuals== | |
| − | |||
| − | |||
| − | === | + | ===CP 3.92=== |
| − | + | <h4>Selection from C.S. Peirce, “Logic Of Relatives” (1870), CP 3.45–149</h4> | |
| − | |||
| − | = | + | <div style="margin-left:25px;"> |
| − | + | 92. Demonstration of the sort called mathematical is founded on suppositions of particular cases. The geometrician draws a figure; the algebraist assumes a letter to signify a single quantity fulfilling the required conditions. But while the mathematician supposes an individual case, his hypothesis is yet perfectly general, because he considers no characters of the individual case but those which must belong to every such case. The advantage of his procedure lies in the fact that the logical laws of individual terms are simpler than those which relate to general terms, because individuals are either identical or mutually exclusive, and cannot intersect or be subordinated to one another as classes can. Mathematical demonstration is not, therefore, more restricted to matters of intuition than any other kind of reasoning. Indeed, logical algebra conclusively proves that mathematics extends over the whole realm of formal logic; and any theory of cognition which cannot be adjusted to this fact must be abandoned. We may reap all the advantages which the mathematician is supposed to derive from intuition by simply making general suppositions of individual cases. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | </div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | <h4>References</h4> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <ul> | |
| + | <li>Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic”, <i>Memoirs of the American Academy of Arts and Sciences</i> 9, 317–378, 26 January 1870. Reprinted, <i>Collected Papers</i> 3.45–149, <i>Chronological Edition</i> 2, 359–429. Online <a href="http://www.jstor.org/stable/25058006" target="_blank">(1)</a> <a href="https://archive.org/details/jstor-25058006" target="_blank">(2)</a> <a href="http://books.google.com/books?id=fFnWmf5oLaoC" target="_blank">(3)</a>.</li> | ||
| − | + | <li>Peirce, C.S., <i>Collected Papers of Charles Sanders Peirce</i>, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.</li> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <li>Peirce, C.S., <i>Writings of Charles S. Peirce : A Chronological Edition</i>, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.</li> | |
| + | </ul> | ||
| − | + | <h4>Resources</h4> | |
| − | + | <ul><li><a href="http://intersci.ss.uci.edu/wiki/index.php/Peirce%27s_1870_Logic_Of_Relatives" target="_blank" title="Peirce's 1870 Logic Of Relatives">Peirce's 1870 Logic Of Relatives</a></li></ul> | |
| − | |||
| − | |||
| − | + | ===CP 3.93=== | |
| − | {| align="center" cellspacing=" | + | {| align="center" cellpadding="0" cellspacing="0" width="90%" |
| | | | ||
| − | < | + | <p>In reference to the doctrine of individuals, two distinctions should be borne in mind. The logical atom, or term not capable of logical division, must be one of which every predicate may be universally affirmed or denied. For, let <math>\mathrm{A}\!</math> be such a term. Then, if it is neither true that all <math>\mathrm{A}\!</math> is <math>\mathrm{X}\!</math> nor that no <math>\mathrm{A}\!</math> is <math>\mathrm{X},\!</math> it must be true that some <math>\mathrm{A}\!</math> is <math>\mathrm{X}\!</math> and some <math>\mathrm{A}\!</math> is not <math>\mathrm{X};\!</math> and therefore <math>\mathrm{A}\!</math> may be divided into <math>\mathrm{A}\!</math> that is <math>\mathrm{X}\!</math> and <math>\mathrm{A}\!</math> that is not <math>\mathrm{X},\!</math> which is contrary to its nature as a logical atom.</p> |
| − | a | + | |
| − | + | <p>Such a term can be realized neither in thought nor in sense.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | a | ||
| − | </ | ||
| − | |||
| − | + | <p>Not in sense, because our organs of sense are special — the eye, for example, not immediately informing us of taste, so that an image on the retina is indeterminate in respect to sweetness and non-sweetness. When I see a thing, I do not see that it is not sweet, nor do I see that it is sweet; and therefore what I see is capable of logical division into the sweet and the not sweet. It is customary to assume that visual images are absolutely determinate in respect to color, but even this may be doubted. I know no facts which prove that there is never the least vagueness in the immediate sensation.</p> | |
| − | + | <p>In thought, an absolutely determinate term cannot be realized, because, not being given by sense, such a concept would have to be formed by synthesis, and there would be no end to the synthesis because there is no limit to the number of possible predicates.</p> | |
| − | + | <p>A logical atom, then, like a point in space, would involve for its precise determination an endless process. We can only say, in a general way, that a term, however determinate, may be made more determinate still, but not that it can be made absolutely determinate. Such a term as “the second Philip of Macedon” is still capable of logical division — into Philip drunk and Philip sober, for example; but we call it individual because that which is denoted by it is in only one place at one time. It is a term not <i>absolutely</i> indivisible, but indivisible as long as we neglect differences of time and the differences which accompany them. Such differences we habitually disregard in the logical division of substances. In the division of relations, etc., we do not, of course, disregard these differences, but we disregard some others. There is nothing to prevent almost any sort of difference from being conventionally neglected in some discourse, and if <math>I\!</math> be a term which in consequence of such neglect becomes indivisible in that discourse, we have in that discourse,</p> | |
| − | + | ||
| − | <math> | + | <p align="center"><math>[I] = 1.\!</math></p> |
| − | + | ||
| − | + | <p>This distinction between the absolutely indivisible and that which is one in number from a particular point of view is shadowed forth in the two words <i>individual</i> (τὸ ἄτομον) and <i>singular</i> (τὸ καθ᾿ ἕκαστον); but as those who have used the word <i>individual</i> have not been aware that absolute individuality is merely ideal, it has come to be used in a more general sense.</p> | |
| − | + | ||
| − | + | <p>(CP 3.93, CE 2, 389–390).</p> | |
| − | + | ||
| − | + | <p>Charles Sanders Peirce, “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic”, <i>Memoirs of the American Academy</i>, Volume 9, pp. 317–378, 26 January 1870, <i>Collected Papers</i> (CP 3.45–149), <i>Chronological Edition</i> (CE 2, 359–429).</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
|} | |} | ||
| − | + | <b>Note.</b> On the square bracket notation used above: Peirce explains this notation at [http://inquiryintoinquiry.com/2014/01/29/peirces-1870-logic-of-relatives-%E2%80%A2-selection-2/ CP 3.65]. | |
| − | {| align="center" cellspacing=" | + | {| align="center" cellpadding="0" cellspacing="0" width="90%" |
| − | | <math> | + | | <p>I propose to denote the number of a logical term by enclosing the term in square brackets, thus, <math>[t].\!</math></p> |
|} | |} | ||
| − | + | The <i>number</i> of an absolute term, as in the case of <math>I,\!</math> is defined as the number of individuals it denotes. | |
| − | == | + | ==Document History== |
| − | + | ===2002 • Peirce List=== | |
| − | + | # http://www.cspeirce.com/peirce-l/12-14-02.htm | |
| + | # http://www.cspeirce.com/peirce-l/12-15-02.htm | ||
| − | + | ===2002–2003 • Ontology List=== | |
| − | + | * http://web.archive.org/web/20070302144532/http://suo.ieee.org/ontology/thrd20.html#04416 | |
| − | + | * http://web.archive.org/web/20070304201457/http://suo.ieee.org/ontology/thrd21.html#04425 | |
| − | + | * http://web.archive.org/web/20070302144532/http://suo.ieee.org/ontology/thrd20.html#04455 | |
| + | * http://web.archive.org/web/20070225053324/http://suo.ieee.org/ontology/thrd22.html#04515 | ||
| + | # http://web.archive.org/web/20070302152249/http://suo.ieee.org/ontology/msg04416.html | ||
| + | # http://web.archive.org/web/20070304003617/http://suo.ieee.org/ontology/msg04417.html | ||
| + | # http://web.archive.org/web/20070303180330/http://suo.ieee.org/ontology/msg04418.html | ||
| + | # http://web.archive.org/web/20070304003631/http://suo.ieee.org/ontology/msg04419.html | ||
| + | # http://web.archive.org/web/20070304003523/http://suo.ieee.org/ontology/msg04421.html | ||
| + | # http://web.archive.org/web/20070304003534/http://suo.ieee.org/ontology/msg04422.html | ||
| + | # http://web.archive.org/web/20070304003546/http://suo.ieee.org/ontology/msg04423.html | ||
| + | # http://web.archive.org/web/20070303180343/http://suo.ieee.org/ontology/msg04424.html | ||
| + | # http://web.archive.org/web/20070304003512/http://suo.ieee.org/ontology/msg04425.html | ||
| + | # http://web.archive.org/web/20070304003646/http://suo.ieee.org/ontology/msg04426.html | ||
| + | # http://web.archive.org/web/20070304003657/http://suo.ieee.org/ontology/msg04427.html | ||
| + | # http://web.archive.org/web/20070303180353/http://suo.ieee.org/ontology/msg04431.html | ||
| + | # http://web.archive.org/web/20070304003707/http://suo.ieee.org/ontology/msg04432.html | ||
| + | # http://web.archive.org/web/20070304003718/http://suo.ieee.org/ontology/msg04435.html | ||
| + | # http://web.archive.org/web/20070304003452/http://suo.ieee.org/ontology/msg04436.html | ||
| + | # http://web.archive.org/web/20070303180403/http://suo.ieee.org/ontology/msg04437.html | ||
| + | # http://web.archive.org/web/20070304003728/http://suo.ieee.org/ontology/msg04438.html | ||
| + | # http://web.archive.org/web/20070303180414/http://suo.ieee.org/ontology/msg04439.html | ||
| + | # http://web.archive.org/web/20070304003423/http://suo.ieee.org/ontology/msg04440.html | ||
| + | # http://web.archive.org/web/20070304003502/http://suo.ieee.org/ontology/msg04441.html | ||
| + | # http://web.archive.org/web/20070304003738/http://suo.ieee.org/ontology/msg04442.html | ||
| + | # http://web.archive.org/web/20070304003748/http://suo.ieee.org/ontology/msg04443.html | ||
| + | # http://web.archive.org/web/20070304003432/http://suo.ieee.org/ontology/msg04444.html | ||
| + | # http://web.archive.org/web/20070303180423/http://suo.ieee.org/ontology/msg04445.html | ||
| + | # http://web.archive.org/web/20070304003758/http://suo.ieee.org/ontology/msg04446.html | ||
| + | # http://web.archive.org/web/20070304003809/http://suo.ieee.org/ontology/msg04447.html | ||
| + | # http://web.archive.org/web/20070304003818/http://suo.ieee.org/ontology/msg04448.html | ||
| + | # http://web.archive.org/web/20070304003829/http://suo.ieee.org/ontology/msg04449.html | ||
| + | # http://web.archive.org/web/20070304003842/http://suo.ieee.org/ontology/msg04450.html | ||
| + | # http://web.archive.org/web/20070304003853/http://suo.ieee.org/ontology/msg04451.html | ||
| + | # http://web.archive.org/web/20070304003903/http://suo.ieee.org/ontology/msg04452.html | ||
| + | # http://web.archive.org/web/20070304003913/http://suo.ieee.org/ontology/msg04453.html | ||
| + | # http://web.archive.org/web/20070304003923/http://suo.ieee.org/ontology/msg04454.html | ||
| + | # http://web.archive.org/web/20070303180434/http://suo.ieee.org/ontology/msg04456.html | ||
| + | # http://web.archive.org/web/20070304003933/http://suo.ieee.org/ontology/msg04457.html | ||
| + | # http://web.archive.org/web/20070304003943/http://suo.ieee.org/ontology/msg04458.html | ||
| + | # http://web.archive.org/web/20070304003954/http://suo.ieee.org/ontology/msg04459.html | ||
| + | # http://web.archive.org/web/20070304004004/http://suo.ieee.org/ontology/msg04462.html | ||
| + | # http://web.archive.org/web/20070304004014/http://suo.ieee.org/ontology/msg04464.html | ||
| + | # http://web.archive.org/web/20070304004024/http://suo.ieee.org/ontology/msg04473.html | ||
| + | # http://web.archive.org/web/20070304004034/http://suo.ieee.org/ontology/msg04478.html | ||
| + | # http://web.archive.org/web/20070303180444/http://suo.ieee.org/ontology/msg04484.html | ||
| + | # http://web.archive.org/web/20070304004044/http://suo.ieee.org/ontology/msg04487.html | ||
| + | # http://web.archive.org/web/20070303180454/http://suo.ieee.org/ontology/msg04488.html | ||
| + | # http://web.archive.org/web/20070304004054/http://suo.ieee.org/ontology/msg04492.html | ||
| + | # http://web.archive.org/web/20070303180504/http://suo.ieee.org/ontology/msg04497.html | ||
| + | # http://web.archive.org/web/20070303180514/http://suo.ieee.org/ontology/msg04498.html | ||
| + | # http://web.archive.org/web/20070304004104/http://suo.ieee.org/ontology/msg04499.html | ||
| + | # http://web.archive.org/web/20070304004114/http://suo.ieee.org/ontology/msg04500.html | ||
| + | # http://web.archive.org/web/20070304004126/http://suo.ieee.org/ontology/msg04501.html | ||
| + | # http://web.archive.org/web/20070304004137/http://suo.ieee.org/ontology/msg04502.html | ||
| + | # http://web.archive.org/web/20070304004147/http://suo.ieee.org/ontology/msg04503.html | ||
| + | # http://web.archive.org/web/20070304004158/http://suo.ieee.org/ontology/msg04504.html | ||
| + | # http://web.archive.org/web/20070303180524/http://suo.ieee.org/ontology/msg04506.html | ||
| + | # http://web.archive.org/web/20070302152300/http://suo.ieee.org/ontology/msg04508.html | ||
| + | # http://web.archive.org/web/20070302152309/http://suo.ieee.org/ontology/msg04509.html | ||
| + | # http://web.archive.org/web/20070302152319/http://suo.ieee.org/ontology/msg04510.html | ||
| + | # http://web.archive.org/web/20070302152329/http://suo.ieee.org/ontology/msg04511.html | ||
| + | # http://web.archive.org/web/20070228081319/http://suo.ieee.org/ontology/msg04512.html | ||
| + | # http://web.archive.org/web/20070228081328/http://suo.ieee.org/ontology/msg04513.html | ||
| + | # http://web.archive.org/web/20070228081356/http://suo.ieee.org/ontology/msg04516.html | ||
| + | # http://web.archive.org/web/20070228081406/http://suo.ieee.org/ontology/msg04517.html | ||
| + | # http://web.archive.org/web/20070228081419/http://suo.ieee.org/ontology/msg04518.html | ||
| + | # http://web.archive.org/web/20070228081429/http://suo.ieee.org/ontology/msg04521.html | ||
| + | # http://web.archive.org/web/20070228081440/http://suo.ieee.org/ontology/msg04539.html | ||
| + | # http://web.archive.org/web/20070228081449/http://suo.ieee.org/ontology/msg04541.html | ||
| + | # http://web.archive.org/web/20070228081501/http://suo.ieee.org/ontology/msg04542.html | ||
| + | # http://web.archive.org/web/20070228081512/http://suo.ieee.org/ontology/msg04543.html | ||
| + | # http://web.archive.org/web/20070228081347/http://suo.ieee.org/ontology/msg04515.html | ||
| − | + | ===2003 • Ontology List • Discussion=== | |
| − | + | * http://web.archive.org/web/20070302144532/http://suo.ieee.org/ontology/thrd20.html#04460 | |
| − | |||
| − | |||
| − | + | <ol start="10"> | |
| + | <li>http://web.archive.org/web/20070305104636/http://suo.ieee.org/ontology/msg04460.html</li> | ||
| + | <li>http://web.archive.org/web/20070305123739/http://suo.ieee.org/ontology/msg04461.html</li> | ||
| + | <li>http://web.archive.org/web/20070305103313/http://suo.ieee.org/ontology/msg04471.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104646/http://suo.ieee.org/ontology/msg04472.html</li> | ||
| + | <li>http://web.archive.org/web/20070305201820/http://suo.ieee.org/ontology/msg04475.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104656/http://suo.ieee.org/ontology/msg04476.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104706/http://suo.ieee.org/ontology/msg04477.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104716/http://suo.ieee.org/ontology/msg04479.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104727/http://suo.ieee.org/ontology/msg04480.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104746/http://suo.ieee.org/ontology/msg04481.html</li> | ||
| + | <li>http://web.archive.org/web/20070307071521/http://suo.ieee.org/ontology/msg04482.html</li> | ||
| + | <li>http://web.archive.org/web/20040730203244/http://suo.ieee.org/ontology/msg04483.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104801/http://suo.ieee.org/ontology/msg04485.html</li> | ||
| + | <li>http://web.archive.org/web/20040729135710/http://suo.ieee.org/ontology/msg04486.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104812/http://suo.ieee.org/ontology/msg04493.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104822/http://suo.ieee.org/ontology/msg04494.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104832/http://suo.ieee.org/ontology/msg04495.html</li> | ||
| + | <li>http://web.archive.org/web/20070305104842/http://suo.ieee.org/ontology/msg04496.html</li> | ||
| + | </ol> | ||
| − | === | + | ===2003 • Arisbe List=== |
| − | + | * http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1453 | |
| − | + | * http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1485 | |
| − | + | * http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1505 | |
| − | + | * http://web.archive.org/web/20140619114718/http://stderr.org/pipermail/arisbe/2003-February/thread.html#1520 | |
| − | + | <ol start="38"> | |
| + | <li>http://web.archive.org/web/20140617201423/http://stderr.org/pipermail/arisbe/2003-January/001453.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011725/http://stderr.org/pipermail/arisbe/2003-January/001454.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011629/http://stderr.org/pipermail/arisbe/2003-January/001457.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011625/http://stderr.org/pipermail/arisbe/2003-January/001461.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011649/http://stderr.org/pipermail/arisbe/2003-January/001467.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011653/http://stderr.org/pipermail/arisbe/2003-January/001470.html</li> | ||
| + | <li>http://web.archive.org/web/20051202053753/http://stderr.org/pipermail/arisbe/2003-January/001471.html</li> | ||
| + | <li>http://web.archive.org/web/20050824084910/http://stderr.org/pipermail/arisbe/2003-January/001475.html</li> | ||
| + | <li>http://web.archive.org/web/20051202075602/http://stderr.org/pipermail/arisbe/2003-January/001480.html</li> | ||
| + | <li>http://web.archive.org/web/20050826203125/http://stderr.org/pipermail/arisbe/2003-January/001481.html</li> | ||
| + | <li>http://web.archive.org/web/20051202045453/http://stderr.org/pipermail/arisbe/2003-January/001482.html</li> | ||
| + | <li>http://web.archive.org/web/20051202035157/http://stderr.org/pipermail/arisbe/2003-January/001483.html</li> | ||
| + | <li>http://web.archive.org/web/20051202053307/http://stderr.org/pipermail/arisbe/2003-January/001484.html</li> | ||
| + | <li>http://web.archive.org/web/20051202042621/http://stderr.org/pipermail/arisbe/2003-January/001485.html</li> | ||
| + | <li>http://web.archive.org/web/20051202070136/http://stderr.org/pipermail/arisbe/2003-January/001486.html</li> | ||
| + | <li>http://web.archive.org/web/20051202011212/http://stderr.org/pipermail/arisbe/2003-January/001488.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090030/http://stderr.org/pipermail/arisbe/2003-January/001489.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090129/http://stderr.org/pipermail/arisbe/2003-January/001503.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090050/http://stderr.org/pipermail/arisbe/2003-January/001505.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090219/http://stderr.org/pipermail/arisbe/2003-January/001507.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090106/http://stderr.org/pipermail/arisbe/2003-January/001513.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090223/http://stderr.org/pipermail/arisbe/2003-January/001514.html</li> | ||
| + | <li>http://web.archive.org/web/20050506090154/http://stderr.org/pipermail/arisbe/2003-January/001515.html</li> | ||
| + | <li>http://web.archive.org/web/20070315211932/http://stderr.org/pipermail/arisbe/2003-February/001520.html</li> | ||
| + | <li>http://web.archive.org/web/20070315211952/http://stderr.org/pipermail/arisbe/2003-February/001525.html</li> | ||
| + | <li>http://web.archive.org/web/20070315212032/http://stderr.org/pipermail/arisbe/2003-February/001529.html</li> | ||
| + | <li>http://web.archive.org/web/20070315212112/http://stderr.org/pipermail/arisbe/2003-February/001534.html</li> | ||
| + | <li>http://web.archive.org/web/20070315163838/http://stderr.org/pipermail/arisbe/2003-February/001567.html</li> | ||
| + | <li>http://web.archive.org/web/20070315212724/http://stderr.org/pipermail/arisbe/2003-February/001578.html</li> | ||
| + | <li>http://web.archive.org/web/20070315212733/http://stderr.org/pipermail/arisbe/2003-February/001579.html</li> | ||
| + | <li>http://web.archive.org/web/20070315212814/http://stderr.org/pipermail/arisbe/2003-February/001587.html</li> | ||
| + | </ol> | ||
| − | + | ===2003 • Arisbe List • Discussion=== | |
| − | + | * http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1455 | |
| − | + | <ol start="12"> | |
| + | <li>http://web.archive.org/web/20051202040453/http://stderr.org/pipermail/arisbe/2003-January/001455.html</li> | ||
| + | <li>http://web.archive.org/web/20050826052233/http://stderr.org/pipermail/arisbe/2003-January/001456.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011705/http://stderr.org/pipermail/arisbe/2003-January/001458.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011657/http://stderr.org/pipermail/arisbe/2003-January/001459.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011857/http://stderr.org/pipermail/arisbe/2003-January/001460.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011701/http://stderr.org/pipermail/arisbe/2003-January/001462.html</li> | ||
| + | <li>http://web.archive.org/web/20050826112404/http://stderr.org/pipermail/arisbe/2003-January/001463.html</li> | ||
| + | <li>http://web.archive.org/web/20051202065741/http://stderr.org/pipermail/arisbe/2003-January/001464.html</li> | ||
| + | <li>http://web.archive.org/web/20050827050454/http://stderr.org/pipermail/arisbe/2003-January/001465.html</li> | ||
| + | <li>http://web.archive.org/web/20051202100823/http://stderr.org/pipermail/arisbe/2003-January/001466.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011801/http://stderr.org/pipermail/arisbe/2003-January/001468.html</li> | ||
| + | <li>http://web.archive.org/web/20050824223011/http://stderr.org/pipermail/arisbe/2003-January/001469.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011633/http://stderr.org/pipermail/arisbe/2003-January/001476.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011849/http://stderr.org/pipermail/arisbe/2003-January/001477.html</li> | ||
| + | <li>http://web.archive.org/web/20050826141451/http://stderr.org/pipermail/arisbe/2003-January/001478.html</li> | ||
| + | <li>http://web.archive.org/web/20050506011845/http://stderr.org/pipermail/arisbe/2003-January/001479.html</li> | ||
| + | </ol> | ||
| − | + | ===2003 • Inquiry List=== | |
| − | + | * http://web.archive.org/web/20150224210000/http://stderr.org/pipermail/inquiry/2003-March/thread.html#186 | |
| + | * http://web.archive.org/web/20150302021003/http://stderr.org/pipermail/inquiry/2003-April/thread.html#245 | ||
| + | # http://web.archive.org/web/20081120062116/http://stderr.org/pipermail/inquiry/2003-March/000186.html | ||
| + | # http://web.archive.org/web/20061013222246/http://stderr.org/pipermail/inquiry/2003-March/000187.html | ||
| + | # http://web.archive.org/web/20061013221536/http://stderr.org/pipermail/inquiry/2003-March/000188.html | ||
| + | # http://web.archive.org/web/20061013222728/http://stderr.org/pipermail/inquiry/2003-March/000189.html | ||
| + | # http://web.archive.org/web/20061013222333/http://stderr.org/pipermail/inquiry/2003-March/000190.html | ||
| + | # http://web.archive.org/web/20061013221823/http://stderr.org/pipermail/inquiry/2003-March/000191.html | ||
| + | # http://web.archive.org/web/20070305235828/http://stderr.org/pipermail/inquiry/2003-March/000194.html | ||
| + | # http://web.archive.org/web/20070302055237/http://stderr.org/pipermail/inquiry/2003-March/000195.html | ||
| + | # http://web.archive.org/web/20070303020850/http://stderr.org/pipermail/inquiry/2003-April/000245.html | ||
| + | # http://web.archive.org/web/20070306225534/http://stderr.org/pipermail/inquiry/2003-April/000246.html | ||
| + | # http://web.archive.org/web/20070315063236/http://stderr.org/pipermail/inquiry/2003-April/000247.html | ||
| + | # http://web.archive.org/web/20070310205044/http://stderr.org/pipermail/inquiry/2003-April/000248.html | ||
| + | # http://web.archive.org/web/20070310205014/http://stderr.org/pipermail/inquiry/2003-April/000249.html | ||
| + | # http://web.archive.org/web/20061013223819/http://stderr.org/pipermail/inquiry/2003-April/000250.html | ||
| + | # http://web.archive.org/web/20070310204954/http://stderr.org/pipermail/inquiry/2003-April/000251.html | ||
| + | # http://web.archive.org/web/20070309174344/http://stderr.org/pipermail/inquiry/2003-April/000252.html | ||
| + | # http://web.archive.org/web/20070310205054/http://stderr.org/pipermail/inquiry/2003-April/000253.html | ||
| + | # http://web.archive.org/web/20070310205024/http://stderr.org/pipermail/inquiry/2003-April/000254.html | ||
| + | # http://web.archive.org/web/20070310205034/http://stderr.org/pipermail/inquiry/2003-April/000255.html | ||
| + | # http://web.archive.org/web/20070310205105/http://stderr.org/pipermail/inquiry/2003-April/000256.html | ||
| + | # http://web.archive.org/web/20070310205116/http://stderr.org/pipermail/inquiry/2003-April/000257.html | ||
| + | # http://web.archive.org/web/20070309174424/http://stderr.org/pipermail/inquiry/2003-April/000258.html | ||
| + | # http://web.archive.org/web/20070311141543/http://stderr.org/pipermail/inquiry/2003-April/000259.html | ||
| + | # http://web.archive.org/web/20070309202630/http://stderr.org/pipermail/inquiry/2003-April/000260.html | ||
| + | # http://web.archive.org/web/20070309202751/http://stderr.org/pipermail/inquiry/2003-April/000261.html | ||
| + | # http://web.archive.org/web/20070309174451/http://stderr.org/pipermail/inquiry/2003-April/000262.html | ||
| + | # http://web.archive.org/web/20070309202431/http://stderr.org/pipermail/inquiry/2003-April/000263.html | ||
| + | # http://web.archive.org/web/20070310204947/http://stderr.org/pipermail/inquiry/2003-April/000264.html | ||
| + | # http://web.archive.org/web/20070309202640/http://stderr.org/pipermail/inquiry/2003-April/000265.html | ||
| + | # http://web.archive.org/web/20070309202441/http://stderr.org/pipermail/inquiry/2003-April/000267.html | ||
| + | # http://web.archive.org/web/20070310205004/http://stderr.org/pipermail/inquiry/2003-April/000268.html | ||
| + | # http://web.archive.org/web/20061013223536/http://stderr.org/pipermail/inquiry/2003-April/000269.html | ||
| + | # http://web.archive.org/web/20070309202731/http://stderr.org/pipermail/inquiry/2003-April/000270.html | ||
| + | # http://web.archive.org/web/20061013223302/http://stderr.org/pipermail/inquiry/2003-April/000271.html | ||
| + | # http://web.archive.org/web/20070310205134/http://stderr.org/pipermail/inquiry/2003-April/000273.html | ||
| + | # http://web.archive.org/web/20070310205146/http://stderr.org/pipermail/inquiry/2003-April/000274.html | ||
| + | # http://web.archive.org/web/20070310075558/http://stderr.org/pipermail/inquiry/2003-April/000275.html | ||
| + | # http://web.archive.org/web/20070309174501/http://stderr.org/pipermail/inquiry/2003-April/000276.html | ||
| + | # http://web.archive.org/web/20070311141604/http://stderr.org/pipermail/inquiry/2003-April/000277.html | ||
| + | # http://web.archive.org/web/20070309202651/http://stderr.org/pipermail/inquiry/2003-April/000278.html | ||
| + | # http://web.archive.org/web/20070311141625/http://stderr.org/pipermail/inquiry/2003-April/000279.html | ||
| + | # http://web.archive.org/web/20070310205157/http://stderr.org/pipermail/inquiry/2003-April/000280.html | ||
| + | # http://web.archive.org/web/20070310205207/http://stderr.org/pipermail/inquiry/2003-April/000281.html | ||
| + | # http://web.archive.org/web/20070309174530/http://stderr.org/pipermail/inquiry/2003-April/000282.html | ||
| + | # http://web.archive.org/web/20070310205217/http://stderr.org/pipermail/inquiry/2003-April/000283.html | ||
| + | # http://web.archive.org/web/20070310205228/http://stderr.org/pipermail/inquiry/2003-April/000284.html | ||
| + | # http://web.archive.org/web/20070309202710/http://stderr.org/pipermail/inquiry/2003-April/000285.html | ||
| + | # http://web.archive.org/web/20070310205237/http://stderr.org/pipermail/inquiry/2003-April/000286.html | ||
| + | # http://web.archive.org/web/20070310205247/http://stderr.org/pipermail/inquiry/2003-April/000287.html | ||
| + | # http://web.archive.org/web/20070309202720/http://stderr.org/pipermail/inquiry/2003-April/000288.html | ||
| + | # http://web.archive.org/web/20061013223711/http://stderr.org/pipermail/inquiry/2003-April/000289.html | ||
| + | # http://web.archive.org/web/20070310205257/http://stderr.org/pipermail/inquiry/2003-April/000290.html | ||
| + | # http://web.archive.org/web/20061013223830/http://stderr.org/pipermail/inquiry/2003-April/000291.html | ||
| + | # http://web.archive.org/web/20070310205307/http://stderr.org/pipermail/inquiry/2003-April/000294.html | ||
| + | # http://web.archive.org/web/20061013224103/http://stderr.org/pipermail/inquiry/2003-April/000295.html | ||
| + | # http://web.archive.org/web/20070310205317/http://stderr.org/pipermail/inquiry/2003-April/000296.html | ||
| + | # http://web.archive.org/web/20070310095852/http://stderr.org/pipermail/inquiry/2003-April/000297.html | ||
| + | # http://web.archive.org/web/20061013223138/http://stderr.org/pipermail/inquiry/2003-April/000298.html | ||
| + | # http://web.archive.org/web/20070310205328/http://stderr.org/pipermail/inquiry/2003-April/000299.html | ||
| + | # http://web.archive.org/web/20061013223241/http://stderr.org/pipermail/inquiry/2003-April/000300.html | ||
| + | # http://web.archive.org/web/20081120085752/http://stderr.org/pipermail/inquiry/2003-April/000301.html | ||
| + | # http://web.archive.org/web/20070310205349/http://stderr.org/pipermail/inquiry/2003-April/000302.html | ||
| + | # http://web.archive.org/web/20070311141532/http://stderr.org/pipermail/inquiry/2003-April/000303.html | ||
| + | # http://web.archive.org/web/20070309203110/http://stderr.org/pipermail/inquiry/2003-April/000305.html | ||
| + | # http://web.archive.org/web/20070310205359/http://stderr.org/pipermail/inquiry/2003-April/000306.html | ||
| + | # http://web.archive.org/web/20070310205409/http://stderr.org/pipermail/inquiry/2003-April/000307.html | ||
| + | # http://web.archive.org/web/20070310204919/http://stderr.org/pipermail/inquiry/2003-April/000308.html | ||
| + | # http://web.archive.org/web/20070310205420/http://stderr.org/pipermail/inquiry/2003-April/000309.html | ||
| − | + | ===2004 • Inquiry List • Selections=== | |
| − | + | * http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1750 | |
| − | + | # http://web.archive.org/web/20060217232934/http://stderr.org/pipermail/inquiry/2004-November/001750.html | |
| + | # http://web.archive.org/web/20081120211119/http://stderr.org/pipermail/inquiry/2004-November/001751.html | ||
| + | # http://web.archive.org/web/20081120205154/http://stderr.org/pipermail/inquiry/2004-November/001752.html | ||
| + | # http://web.archive.org/web/20060217232947/http://stderr.org/pipermail/inquiry/2004-November/001753.html | ||
| + | # http://web.archive.org/web/20081120202444/http://stderr.org/pipermail/inquiry/2004-November/001754.html | ||
| + | # http://web.archive.org/web/20081120202147/http://stderr.org/pipermail/inquiry/2004-November/001760.html | ||
| + | # http://web.archive.org/web/20081120191806/http://stderr.org/pipermail/inquiry/2004-November/001769.html | ||
| + | # http://web.archive.org/web/20081120212429/http://stderr.org/pipermail/inquiry/2004-November/001774.html | ||
| + | # http://web.archive.org/web/20120222231523/http://stderr.org/pipermail/inquiry/2004-November/001783.html | ||
| + | # http://web.archive.org/web/20120222231525/http://stderr.org/pipermail/inquiry/2004-November/001794.html | ||
| + | # http://web.archive.org/web/20060217233454/http://stderr.org/pipermail/inquiry/2004-November/001812.html | ||
| + | # http://web.archive.org/web/20060217233731/http://stderr.org/pipermail/inquiry/2004-November/001842.html | ||
| + | ===2004 • Inquiry List • Comments=== | ||
| − | + | * http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1755 | |
| − | + | {| | |
| − | + | |- | |
| − | + | | align=right | 1. || http://web.archive.org/web/20060217233003/http://stderr.org/pipermail/inquiry/2004-November/001755.html | |
| − | + | |- | |
| − | + | | align=right | 2. || http://web.archive.org/web/20060217233011/http://stderr.org/pipermail/inquiry/2004-November/001756.html | |
| − | + | |- | |
| − | + | | align=right | 3. || http://web.archive.org/web/20081120200505/http://stderr.org/pipermail/inquiry/2004-November/001757.html | |
| − | + | |- | |
| − | + | | align=right | 4. || http://web.archive.org/web/20081120200000/http://stderr.org/pipermail/inquiry/2004-November/001758.html | |
| − | + | |- | |
| − | + | | align=right | 5. || http://web.archive.org/web/20060217233024/http://stderr.org/pipermail/inquiry/2004-November/001759.html | |
| − | + | |- | |
| − | + | | align=right | 6. || http://web.archive.org/web/20120222231542/http://stderr.org/pipermail/inquiry/2004-November/001761.html | |
| − | + | |- | |
| − | + | | align=right | 7. || http://web.archive.org/web/20120222231543/http://stderr.org/pipermail/inquiry/2004-November/001770.html | |
| − | + | |- | |
| − | + | | align=right | 8.1. || http://web.archive.org/web/20120222231545/http://stderr.org/pipermail/inquiry/2004-November/001775.html | |
| − | + | |- | |
| − | + | | align=right | 8.2. || http://web.archive.org/web/20120222231547/http://stderr.org/pipermail/inquiry/2004-November/001776.html | |
| − | + | |- | |
| − | + | | align=right | 8.3. || http://web.archive.org/web/20120222231549/http://stderr.org/pipermail/inquiry/2004-November/001777.html | |
| − | + | |- | |
| − | + | | align=right | 8.4. || http://web.archive.org/web/20120222231551/http://stderr.org/pipermail/inquiry/2004-November/001778.html | |
| − | + | |- | |
| − | + | | align=right | 8.5. || http://web.archive.org/web/20120222231553/http://stderr.org/pipermail/inquiry/2004-November/001781.html | |
| − | + | |- | |
| − | + | | align=right | 8.6. || http://web.archive.org/web/20120222231555/http://stderr.org/pipermail/inquiry/2004-November/001782.html | |
| − | + | |- | |
| − | + | | align=right | 9.1. || http://web.archive.org/web/20120222231557/http://stderr.org/pipermail/inquiry/2004-November/001787.html | |
| − | + | |- | |
| − | + | | align=right | 9.2. || http://web.archive.org/web/20120222231559/http://stderr.org/pipermail/inquiry/2004-November/001788.html | |
| − | + | |- | |
| − | + | | align=right | 9.3. || http://web.archive.org/web/20120222231601/http://stderr.org/pipermail/inquiry/2004-November/001789.html | |
| − | + | |- | |
| − | + | | align=right | 9.4. || http://web.archive.org/web/20120222231604/http://stderr.org/pipermail/inquiry/2004-November/001790.html | |
| − | + | |- | |
| − | + | | align=right | 9.5. || http://web.archive.org/web/20120222231606/http://stderr.org/pipermail/inquiry/2004-November/001791.html | |
| − | + | |- | |
| − | + | | align=right | 9.6. || http://web.archive.org/web/20120222231608/http://stderr.org/pipermail/inquiry/2004-November/001792.html | |
| − | + | |- | |
| − | + | | align=right | 9.7. || http://web.archive.org/web/20120222231610/http://stderr.org/pipermail/inquiry/2004-November/001793.html | |
| − | + | |- | |
| − | + | | align=right | 10.01. || http://web.archive.org/web/20120222231611/http://stderr.org/pipermail/inquiry/2004-November/001795.html | |
| − | + | |- | |
| − | + | | align=right | 10.02. || http://web.archive.org/web/20120222231613/http://stderr.org/pipermail/inquiry/2004-November/001796.html | |
| − | + | |- | |
| − | + | | align=right | 10.03. || http://web.archive.org/web/20120222231615/http://stderr.org/pipermail/inquiry/2004-November/001797.html | |
| − | + | |- | |
| − | + | | align=right | 10.04. || http://web.archive.org/web/20120222231617/http://stderr.org/pipermail/inquiry/2004-November/001798.html | |
| − | + | |- | |
| − | + | | align=right | 10.05. || http://web.archive.org/web/20120222231619/http://stderr.org/pipermail/inquiry/2004-November/001799.html | |
| − | + | |- | |
| − | + | | align=right | 10.06. || http://web.archive.org/web/20120222231621/http://stderr.org/pipermail/inquiry/2004-November/001800.html | |
| − | + | |- | |
| − | + | | align=right | 10.07. || http://web.archive.org/web/20120222231623/http://stderr.org/pipermail/inquiry/2004-November/001801.html | |
| − | + | |- | |
| − | + | | align=right | 10.08. || http://web.archive.org/web/20120222231625/http://stderr.org/pipermail/inquiry/2004-November/001802.html | |
| − | + | |- | |
| − | + | | align=right | 10.09. || http://web.archive.org/web/20120222231627/http://stderr.org/pipermail/inquiry/2004-November/001803.html | |
| − | | | + | |- |
| − | + | | align=right | 10.10. || http://web.archive.org/web/20120222231629/http://stderr.org/pipermail/inquiry/2004-November/001804.html | |
| − | | | + | |- |
| − | + | | align=right | 10.11. || http://web.archive.org/web/20120222231829/http://stderr.org/pipermail/inquiry/2004-November/001805.html | |
| − | | | + | |- |
| − | + | | align=right | 11.01. || http://web.archive.org/web/20060217233458/http://stderr.org/pipermail/inquiry/2004-November/001813.html | |
| − | + | |- | |
| − | + | | align=right | 11.02. || http://web.archive.org/web/20051215103907/http://stderr.org/pipermail/inquiry/2004-November/001814.html | |
| − | + | |- | |
| − | + | | align=right | 11.03. || http://web.archive.org/web/20120222231842/http://stderr.org/pipermail/inquiry/2004-November/001815.html | |
| − | + | |- | |
| − | + | | align=right | 11.04. || http://web.archive.org/web/20120222231853/http://stderr.org/pipermail/inquiry/2004-November/001816.html | |
| − | + | |- | |
| − | + | | align=right | 11.05. || http://web.archive.org/web/20060217233520/http://stderr.org/pipermail/inquiry/2004-November/001817.html | |
| − | + | |- | |
| − | + | | align=right | 11.06. || http://web.archive.org/web/20060217233527/http://stderr.org/pipermail/inquiry/2004-November/001818.html | |
| − | + | |- | |
| − | + | | align=right | 11.07. || http://web.archive.org/web/20120222231859/http://stderr.org/pipermail/inquiry/2004-November/001819.html | |
| − | + | |- | |
| − | + | | align=right | 11.08. || http://web.archive.org/web/20120222231901/http://stderr.org/pipermail/inquiry/2004-November/001820.html | |
| − | + | |- | |
| − | + | | align=right | 11.09. || http://web.archive.org/web/20120222231903/http://stderr.org/pipermail/inquiry/2004-November/001821.html | |
| − | + | |- | |
| − | + | | align=right | 11.10. || http://web.archive.org/web/20120222231905/http://stderr.org/pipermail/inquiry/2004-November/001822.html | |
| − | + | |- | |
| − | + | | align=right | 11.11. || http://web.archive.org/web/20120222231907/http://stderr.org/pipermail/inquiry/2004-November/001823.html | |
| − | + | |- | |
| − | + | | align=right | 11.12. || http://web.archive.org/web/20120222231909/http://stderr.org/pipermail/inquiry/2004-November/001824.html | |
| − | + | |- | |
| − | + | | align=right | 11.13. || http://web.archive.org/web/20120222232025/http://stderr.org/pipermail/inquiry/2004-November/001825.html | |
| − | + | |- | |
| − | + | | align=right | 11.14. || http://web.archive.org/web/20120222232029/http://stderr.org/pipermail/inquiry/2004-November/001826.html | |
| − | + | |- | |
| − | + | | align=right | 11.15. || http://web.archive.org/web/20120222232030/http://stderr.org/pipermail/inquiry/2004-November/001827.html | |
| − | + | |- | |
| − | + | | align=right | 11.16. || http://web.archive.org/web/20120222232032/http://stderr.org/pipermail/inquiry/2004-November/001828.html | |
| − | + | |- | |
| − | + | | align=right | 11.17. || http://web.archive.org/web/20120222232035/http://stderr.org/pipermail/inquiry/2004-November/001829.html | |
| − | + | |- | |
| − | + | | align=right | 11.18. || http://web.archive.org/web/20120222232037/http://stderr.org/pipermail/inquiry/2004-November/001830.html | |
| − | + | |- | |
| − | + | | align=right | 11.19. || http://web.archive.org/web/20120222232041/http://stderr.org/pipermail/inquiry/2004-November/001831.html | |
| − | + | |- | |
| − | + | | align=right | 11.20. || http://web.archive.org/web/20120222232043/http://stderr.org/pipermail/inquiry/2004-November/001832.html | |
| − | + | |- | |
| − | + | | align=right | 11.21. || http://web.archive.org/web/20120222232044/http://stderr.org/pipermail/inquiry/2004-November/001833.html | |
| − | + | |- | |
| − | + | | align=right | 11.22. || http://web.archive.org/web/20120222232046/http://stderr.org/pipermail/inquiry/2004-November/001834.html | |
| − | + | |- | |
| − | + | | align=right | 11.23. || http://web.archive.org/web/20120222232048/http://stderr.org/pipermail/inquiry/2004-November/001835.html | |
| − | + | |- | |
| − | + | | align=right | 11.24. || http://web.archive.org/web/20120222232049/http://stderr.org/pipermail/inquiry/2004-November/001836.html | |
| − | + | |- | |
| − | + | | align=right | 12. || http://web.archive.org/web/20060217233738/http://stderr.org/pipermail/inquiry/2004-November/001843.html | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===2004–2009 • Inquiry List • Discussion=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768 | |
| − | + | * http://web.archive.org/web/20061013215458/http://stderr.org/pipermail/inquiry/2005-January/thread.html#2301 | |
| − | + | * http://web.archive.org/web/20120428203121/http://stderr.org/pipermail/inquiry/2009-April/thread.html#3548 | |
| − | |||
| − | |||
| − | |||
| − | + | <ol start="28"> | |
| − | + | <li>http://web.archive.org/web/20120222232055/http://stderr.org/pipermail/inquiry/2004-November/001768.html</li> | |
| − | + | <li>http://web.archive.org/web/20120222232057/http://stderr.org/pipermail/inquiry/2004-November/001838.html</li> | |
| − | + | <li>http://web.archive.org/web/20120222232101/http://stderr.org/pipermail/inquiry/2004-November/001840.html</li> | |
| − | + | <li>http://web.archive.org/web/20061014002508/http://stderr.org/pipermail/inquiry/2005-January/002301.html</li> | |
| − | + | <li>http://web.archive.org/web/20120206222034/http://stderr.org/pipermail/inquiry/2009-April/003548.html</li> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <ol start=" | ||
| − | <li>http:// | ||
| − | |||
| − | |||
| − | <li>http:// | ||
| − | |||
| − | |||
| − | |||
| − | <li>http:// | ||
| − | |||
| − | |||
| − | <li>http:// | ||
| − | |||
| − | |||
| − | <li>http:// | ||
| − | |||
| − | |||
</ol> | </ol> | ||
| − | === | + | ===2007 • MyWikiBiz Copy=== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * http:// | + | * [http://mywikibiz.com/User:Jon_Awbrey Jon Awbrey] • [http://mywikibiz.com/index.php?title=Directory_talk:Jon_Awbrey/Papers/Peirce%27s_1870_Logic_Of_Relatives&oldid=51117 Peirce's 1870 Logic Of Relatives • 10 October 2007] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 21:24, 21 February 2017
Author: Jon Awbrey
Peirce's text employs lower case letters for logical terms of general reference and upper case letters for logical terms of individual reference. General terms fall into types — absolute terms, dyadic relative terms, higher adic relative terms — and Peirce employs different typefaces to distinguish these. The following Tables indicate the typefaces that are used in the text below for Peirce's examples of general terms.
|
\(\begin{array}{ll} \mathrm{a}. & \text{animal} \\ \mathrm{b}. & \text{black} \\ \mathrm{f}. & \text{Frenchman} \\ \mathrm{h}. & \text{horse} \\ \mathrm{m}. & \text{man} \\ \mathrm{p}. & \text{President of the United States Senate} \\ \mathrm{r}. & \text{rich person} \\ \mathrm{u}. & \text{violinist} \\ \mathrm{v}. & \text{Vice-President of the United States} \\ \mathrm{w}. & \text{woman} \end{array}\) |
|
\(\begin{array}{ll} \mathit{a}. & \text{enemy} \\ \mathit{b}. & \text{benefactor} \\ \mathit{c}. & \text{conqueror} \\ \mathit{e}. & \text{emperor} \\ \mathit{h}. & \text{husband} \\ \mathit{l}. & \text{lover} \\ \mathit{m}. & \text{mother} \\ \mathit{n}. & \text{not} \\ \mathit{o}. & \text{owner} \\ \mathit{s}. & \text{servant} \\ \mathit{w}. & \text{wife} \end{array}\) |
|
\(\begin{array}{ll} \mathfrak{b}. & \text{betrayer to ------ of ------} \\ \mathfrak{g}. & \text{giver to ------ of ------} \\ \mathfrak{t}. & \text{transferrer from ------ to ------} \\ \mathfrak{w}. & \text{winner over of ------ to ------ from ------} \end{array}\) |
Individual terms are taken to denote individual entities falling under a general term. Peirce uses upper case Roman letters for individual terms, for example, the individual horses \(\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}\) falling under the general term \(\mathrm{h}\!\) for horse.
The path to understanding Peirce's system and its wider implications for logic can be smoothed by paraphrasing his notations in a variety of contemporary mathematical formalisms, while preserving the semantics as much as possible. Remaining faithful to Peirce's orthography while adding parallel sets of stylistic conventions will, however, demand close attention to typography-in-context. Current style sheets for mathematical texts specify italics for mathematical variables, with upper case letters for sets and lower case letters for individuals. So we need to keep an eye out for the difference between the individual \(\mathrm{X}\!\) of the genus \(\mathrm{x}\!\) and the element \(x\!\) of the set \(X\!\) as we pass between the two styles of text.
Selection 1
Use of the Letters
|
The letters of the alphabet will denote logical signs. Now logical terms are of three grand classes. The first embraces those whose logical form involves only the conception of quality, and which therefore represent a thing simply as “a ——”. These discriminate objects in the most rudimentary way, which does not involve any consciousness of discrimination. They regard an object as it is in itself as such (quale); for example, as horse, tree, or man. These are absolute terms. The second class embraces terms whose logical form involves the conception of relation, and which require the addition of another term to complete the denotation. These discriminate objects with a distinct consciousness of discrimination. They regard an object as over against another, that is as relative; as father of, lover of, or servant of. These are simple relative terms. The third class embraces terms whose logical form involves the conception of bringing things into relation, and which require the addition of more than one term to complete the denotation. They discriminate not only with consciousness of discrimination, but with consciousness of its origin. They regard an object as medium or third between two others, that is as conjugative; as giver of —— to ——, or buyer of —— for —— from ——. These may be termed conjugative terms. The conjugative term involves the conception of third, the relative that of second or other, the absolute term simply considers an object. No fourth class of terms exists involving the conception of fourth, because when that of third is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. Whether this reason for the fact that there is no fourth class of terms fundamentally different from the third is satisfactory of not, the fact itself is made perfectly evident by the study of the logic of relatives. (Peirce, CP 3.63). |
I am going to experiment with an interlacing commentary on Peirce's 1870 “Logic of Relatives” paper, revisiting some critical transitions from several different angles and calling attention to a variety of puzzles, problems, and potentials that are not so often remarked or tapped.
What strikes me about the initial installment this time around is its use of a certain pattern of argument that I can recognize as invoking a closure principle, and this is a figure of reasoning that Peirce uses in three other places: his discussion of continuous predicates, his definition of sign relations, and in the pragmatic maxim itself.
One might also call attention to the following two statements:
|
Now logical terms are of three grand classes. |
|
No fourth class of terms exists involving the conception of fourth, because when that of third is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. |
Selection 2
Numbers Corresponding to Letters
|
I propose to use the term “universe” to denote that class of individuals about which alone the whole discourse is understood to run. The universe, therefore, in this sense, as in Mr. De Morgan's, is different on different occasions. In this sense, moreover, discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains. I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (men), the number of “tooth of” would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus \([t].\!\) (Peirce, CP 3.65). |
Peirce's remarks at CP 3.65 are so replete with remarkable ideas, some of them so taken for granted in mathematical discourse that they usually escape explicit mention, and others so suggestive of things to come in a future remote from his time of writing, and yet so smoothly introduced in passing that it's all too easy to overlook their consequential significance, that I can do no better here than to highlight these ideas in other words, whose main advantage is to be a little more jarring to the mind's sensibilities.
- This mapping of letters to numbers, or logical terms to mathematical quantities, is the very core of what "quantification theory" is all about, and definitely more to the point than the mere "innovation" of using distinctive symbols for the so-called "quantifiers". We will speak of this more later on.
- The mapping of logical terms to numerical measures, to express it in current language, would probably be recognizable as some kind of "morphism" or "functor" from a logical domain to a quantitative co-domain.
- Notice that Peirce follows the mathematician's usual practice, then and now, of making the status of being an "individual" or a "universal" relative to a discourse in progress. I have come to appreciate more and more of late how radically different this "patchwork" or "piecewise" approach to things is from the way of some philosophers who seem to be content with nothing less than many worlds domination, which means that they are never content and rarely get started toward the solution of any real problem. Just my observation, I hope you understand.
- It is worth noting that Peirce takes the "plural denotation" of terms for granted, or what's the number of a term for, if it could not vary apart from being one or nil?
- I also observe that Peirce takes the individual objects of a particular universe of discourse in a "generative" way, not a "totalizing" way, and thus they afford us with the basis for talking freely about collections, constructions, properties, qualities, subsets, and "higher types", as the phrase is mint.
Selection 3
The Signs of Inclusion, Equality, Etc.
|
I shall follow Boole in taking the sign of equality to signify identity. Thus, if \(\mathrm{v}\!\) denotes the Vice-President of the United States, and \(\mathrm{p}~\!\) the President of the Senate of the United States, | |||||||||
| \(\mathrm{v} = \mathrm{p}\!\) | |||||||||
|
means that every Vice-President of the United States is President of the Senate, and every President of the United States Senate is Vice-President. The sign “less than” is to be so taken that | |||||||||
| \(\mathrm{f} < \mathrm{m}~\!\) | |||||||||
|
means that every Frenchman is a man, but there are men besides Frenchmen. Drobisch has used this sign in the same sense. It will follow from these significations of \(=\!\) and \(<\!\) that the sign \(-\!\!\!<\!\) (or \(\leqq\), “as small as”) will mean “is”. Thus, | |||||||||
| \(\mathrm{f} ~-\!\!\!< \mathrm{m}\) | |||||||||
|
means “every Frenchman is a man”, without saying whether there are any other men or not. So, | |||||||||
| \(\mathit{m} ~-\!\!\!< \mathit{l}\) | |||||||||
|
will mean that every mother of anything is a lover of the same thing; although this interpretation in some degree anticipates a convention to be made further on. These significations of \(=\!\) and \(<\!\) plainly conform to the indispensable conditions. Upon the transitive character of these relations the syllogism depends, for by virtue of it, from | |||||||||
| |||||||||
|
that is, from every Frenchman being a man and every man being an animal, that every Frenchman is an animal. But not only do the significations of \(=\!\) and \(<\!\) here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. So, to write \(5 < 7\!\) is to say that \(5\!\) is part of \(7\!\), just as to write \(\mathrm{f} < \mathrm{m}~\!\) is to say that Frenchmen are part of men. Indeed, if \(\mathrm{f} < \mathrm{m}~\!\), then the number of Frenchmen is less than the number of men, and if \(\mathrm{v} = \mathrm{p}\!\), then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities. (Peirce, CP 3.66). |
The quantifier mapping from terms to their numbers that Peirce signifies by means of the square bracket notation \([t]\!\) has one of its principal uses in providing a basis for the computation of frequencies, probabilities, and all of the other statistical measures that can be constructed from these, and thus in affording what may be called a principle of correspondence between probability theory and its limiting case in the forms of logic.
This brings us once again to the relativity of contingency and necessity, as one way of approaching necessity is through the avenue of probability, describing necessity as a probability of 1, but the whole apparatus of probability theory only figures in if it is cast against the backdrop of probability space axioms, the reference class of distributions, and the sample space that we cannot help but to abduce upon the scene of observations. Aye, there's the snake eyes. And with them we can see that there is always an irreducible quantum of facticity to all our necessities. More plainly spoken, it takes a fairly complex conceptual infrastructure just to begin speaking of probabilities, and this setting can only be set up by means of abductive, fallible, hypothetical, and inherently risky mental acts.
Pragmatic thinking is the logic of abduction, which is just another way of saying that it addresses the question: “What may be hoped?” We have to face the possibility that it may be just as impossible to speak of “absolute identity” with any hope of making practical philosophical sense as it is to speak of “absolute simultaneity” with any hope of making operational physical sense.
Selection 4
The Signs for Addition
|
The sign of addition is taken by Boole so that |
| \(x + y\!\) |
|
denotes everything denoted by \(x\!\), and, besides, everything denoted by \(y\!\). Thus |
| \(\mathrm{m} + \mathrm{w}~\!\) |
|
denotes all men, and, besides, all women. This signification for this sign is needed for connecting the notation of logic with that of the theory of probabilities. But if there is anything which is denoted by both terms of the sum, the latter no longer stands for any logical term on account of its implying that the objects denoted by one term are to be taken besides the objects denoted by the other. For example, |
| \(\mathrm{f} + \mathrm{u}\!\) |
|
means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are besides themselves. For this reason alone, in a paper which is published in the Proceedings of the Academy for March 17, 1867, I preferred to take as the regular addition of logic a non-invertible process, such that |
| \(\mathrm{m} ~+\!\!,~ \mathrm{b}\) |
|
stands for all men and black things, without any implication that the black things are to be taken besides the men; and the study of the logic of relatives has supplied me with other weighty reasons for the same determination. Since the publication of that paper, I have found that Mr. W. Stanley Jevons, in a tract called Pure Logic, or the Logic of Quality [1864], had anticipated me in substituting the same operation for Boole's addition, although he rejects Boole's operation entirely and writes the new one with a \(+\!\) sign while withholding from it the name of addition. It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions. But the notation has other recommendations. The conception of taking together involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five. Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive. Addition being taken in this sense, nothing is to be denoted by zero, for then |
| \(x ~+\!\!,~ 0 ~=~ x\) |
|
whatever is denoted by \(x\!\); and this is the definition of zero. This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of zero and that of nothing, and because we shall thus have |
| \([0] ~=~ 0.\) |
|
(Peirce, CP 3.67). |
A wealth of issues arises here that I hope to take up in depth at a later point, but for the moment I shall be able to mention only the barest sample of them in passing.
The two papers that precede this one in CP 3 are Peirce's papers of March and September 1867 in the Proceedings of the American Academy of Arts and Sciences, titled “On an Improvement in Boole's Calculus of Logic” and “Upon the Logic of Mathematics”, respectively. Among other things, these two papers provide us with further clues about the motivating considerations that brought Peirce to introduce the “number of a term” function, signified here by square brackets. I have already quoted from the “Logic of Mathematics” paper in a related connection. Here are the links to those excerpts:
In setting up a correspondence between “letters” and “numbers”, Peirce constructs a structure-preserving map from a logical domain to a numerical domain. That he does this deliberately is evidenced by the care that he takes with the conditions under which the chosen aspects of structure are preserved, along with his recognition of the critical fact that zeroes are preserved by the mapping.
Incidentally, Peirce appears to have an inkling of the problems that would later be caused by using the plus sign for inclusive disjunction, but his advice was overridden by the dialects of applied logic that developed in various communities, retarding the exchange of information among engineering, mathematical, and philosophical specialties all throughout the subsequent century.
Selection 5
The Signs for Multiplication
|
I shall adopt for the conception of multiplication the application of a relation, in such a way that, for example, \(\mathit{l}\mathrm{w}~\!\) shall denote whatever is lover of a woman. This notation is the same as that used by Mr. De Morgan, although he appears not to have had multiplication in his mind. \(\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w})\) will, then, denote whatever is servant of anything of the class composed of men and women taken together. So that: |
| \(\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w}) ~=~ \mathit{s}\mathrm{m} ~+\!\!,~ \mathit{s}\mathrm{w}.\) |
|
\((\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w}\) will denote whatever is lover or servant to a woman, and: |
| \((\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w} ~=~ \mathit{l}\mathrm{w} ~+\!\!,~ \mathit{s}\mathrm{w}.\) |
|
\((\mathit{s}\mathit{l})\mathrm{w}\!\) will denote whatever stands to a woman in the relation of servant of a lover, and: |
| \((\mathit{s}\mathit{l})\mathrm{w} ~=~ \mathit{s}(\mathit{l}\mathrm{w}).\) |
|
Thus all the absolute conditions of multiplication are satisfied. The term “identical with ——” is a unity for this multiplication. That is to say, if we denote “identical with ——” by \(\mathit{1}\!\) we have: |
| \(x \mathit{1} ~=~ x ~ ,\) |
|
whatever relative term \(x\!\) may be. For what is a lover of something identical with anything, is the same as a lover of that thing. (Peirce, CP 3.68). |
Peirce in 1870 is five years down the road from the Peirce of 1865–1866 who lectured extensively on the role of sign relations in the logic of scientific inquiry, articulating their involvement in the three types of inference, and inventing the concept of “information” to explain what it is that signs convey in the process. By this time, then, the semiotic or sign relational approach to logic is so implicit in his way of working that he does not always take the trouble to point out its distinctive features at each and every turn. So let's take a moment to draw out a few of these characters.
Sign relations, like any brand of non-trivial 3-adic relations, can become overwhelming to think about once the cardinality of the object, sign, and interpretant domains or the complexity of the relation itself ascends beyond the simplest examples. Furthermore, most of the strategies that we would normally use to control the complexity, like neglecting one of the domains, in effect, projecting the 3-adic sign relation onto one of its 2-adic faces, or focusing on a single ordered triple of the form \((o, s, i)\!\) at a time, can result in our receiving a distorted impression of the sign relation's true nature and structure.
I find that it helps me to draw, or at least to imagine drawing, diagrams of the following form, where I can keep tabs on what's an object, what's a sign, and what's an interpretant sign, for a selected set of sign-relational triples.
Here is how I would picture Peirce's example of equivalent terms, \(\mathrm{v} = \mathrm{p},\!\) where \({}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!\) denotes the Vice-President of the United States, and \({}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!\) denotes the President of the Senate of the United States.
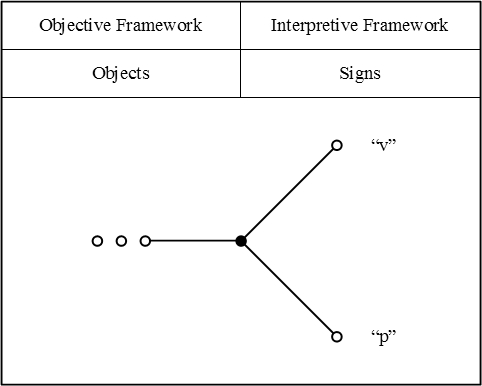
|
| \(\text{Figure 1}~\!\) |
Depending on whether we interpret the terms \({}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!\) and \({}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!\) as applying to persons who hold these offices at one particular time or as applying to all those persons who have held these offices over an extended period of history, their denotations may be either singular of plural, respectively.
As a shortcut technique for indicating general denotations or plural referents, I will use the elliptic convention that represents these by means of figures like “o o o” or “o … o”, placed at the object ends of sign relational triads.
For a more complex example, here is how I would picture Peirce's example of an equivalence between terms that comes about by applying one of the distributive laws, for relative multiplication over absolute summation.
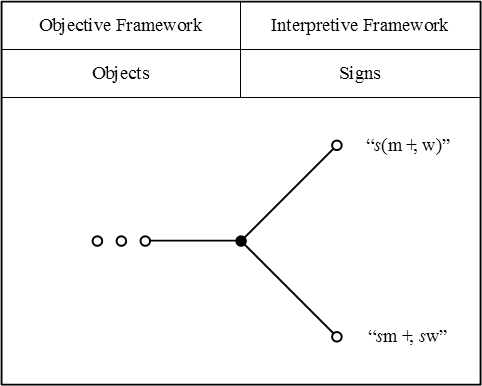
|
| \(\text{Figure 2}\!\) |
Selection 6
The Signs for Multiplication (cont.)
|
A conjugative term like giver naturally requires two correlates, one denoting the thing given, the other the recipient of the gift. We must be able to distinguish, in our notation, the giver of \(\mathrm{A}\!\) to \(\mathrm{B}\!\) from the giver to \(\mathrm{A}\!\) of \(\mathrm{B}\!\), and, therefore, I suppose the signification of the letter equivalent to such a relative to distinguish the correlates as first, second, third, etc., so that “giver of —— to ——” and “giver to —— of ——” will be expressed by different letters. Let \(\mathfrak{g}\) denote the latter of these conjugative terms. Then, the correlates or multiplicands of this multiplier cannot all stand directly after it, as is usual in multiplication, but may be ranged after it in regular order, so that: |
| \(\mathfrak{g}\mathit{x}\mathit{y}\) |
|
will denote a giver to \(\mathit{x}\!\) of \(\mathit{y}\!\). But according to the notation, \(\mathit{x}\!\) here multiplies \(\mathit{y}\!\), so that if we put for \(\mathit{x}\!\) owner (\(\mathit{o}\!\)), and for \(\mathit{y}\!\) horse (\(\mathrm{h}\!\)), |
| \(\mathfrak{g}\mathit{o}\mathrm{h}\) |
|
appears to denote the giver of a horse to an owner of a horse. But let the individual horses be \(\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}\), etc. Then: |
| \(\mathrm{h} ~=~ \mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}\) |
| \(\mathfrak{g}\mathit{o}\mathrm{h} ~=~ \mathfrak{g}\mathit{o}(\mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}) ~=~ \mathfrak{g}\mathit{o}\mathrm{H} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}\) |
|
Now this last member must be interpreted as a giver of a horse to the owner of that horse, and this, therefore must be the interpretation of \(\mathfrak{g}\mathit{o}\mathrm{h}\). This is always very important. A term multiplied by two relatives shows that the same individual is in the two relations. If we attempt to express the giver of a horse to a lover of a woman, and for that purpose write: |
| \(\mathfrak{g}\mathit{l}\mathrm{w}\mathrm{h}\), |
|
we have written giver of a woman to a lover of her, and if we add brackets, thus, |
| \(\mathfrak{g}(\mathit{l}\mathrm{w})\mathrm{h}\), |
|
we abandon the associative principle of multiplication. A little reflection will show that the associative principle must in some form or other be abandoned at this point. But while this principle is sometimes falsified, it oftener holds, and a notation must be adopted which will show of itself when it holds. We already see that we cannot express multiplication by writing the multiplicand directly after the multiplier; let us then affix subjacent numbers after letters to show where their correlates are to be found. The first number shall denote how many factors must be counted from left to right to reach the first correlate, the second how many more must be counted to reach the second, and so on. Then, the giver of a horse to a lover of a woman may be written: |
| \(\mathfrak{g}_{12} \mathit{l}_1 \mathrm{w} \mathrm{h} ~=~ \mathfrak{g}_{11} \mathit{l}_2 \mathrm{h} \mathrm{w} ~=~ \mathfrak{g}_{2(-1)} \mathrm{h} \mathit{l}_1 \mathrm{w}\). |
|
Of course a negative number indicates that the former correlate follows the latter by the corresponding positive number. A subjacent zero makes the term itself the correlate. Thus, |
| \(\mathit{l}_0\!\) |
|
denotes the lover of that lover or the lover of himself, just as \(\mathfrak{g}\mathit{o}\mathrm{h}\) denotes that the horse is given to the owner of itself, for to make a term doubly a correlate is, by the distributive principle, to make each individual doubly a correlate, so that: |
| \(\mathit{l}_0 ~=~ \mathit{L}_0 ~+\!\!,~ \mathit{L}_0^{\prime} ~+\!\!,~ \mathit{L}_0^{\prime\prime} ~+\!\!,~ \text{etc.}\) |
|
A subjacent sign of infinity may indicate that the correlate is indeterminate, so that: |
| \(\mathit{l}_\infty\) |
|
will denote a lover of something. We shall have some confirmation of this presently. If the last subjacent number is a one it may be omitted. Thus we shall have: |
| \(\mathit{l}_1 ~=~ \mathit{l}\), |
| \(\mathfrak{g}_{11} ~=~ \mathfrak{g}_1 ~=~ \mathfrak{g}\). |
|
This enables us to retain our former expressions \(\mathit{l}\mathrm{w}~\!\), \(\mathfrak{g}\mathit{o}\mathrm{h}\), etc. (Peirce, CP 3.69–70). |
Comment : Sets as Logical Sums
Peirce's way of representing sets as logical sums may seem archaic, but it is quite often used, and is actually the tool of choice in many branches of algebra, combinatorics, computing, and statistics to this very day.
Peirce's application to logic is fairly novel, and the degree of his elaboration of the logic of relative terms is certainly original with him, but this particular genre of representation, commonly going under the handle of generating functions, goes way back, well before anyone thought to stick a flag in set theory as a separate territory or to try to fence off our native possessions of it with expressly decreed axioms. And back in the days when a computer was just a person who computed, before we had the sorts of electronic register machines that we take so much for granted today, mathematicians were constantly using generating functions as a rough and ready type of addressable memory to sort, store, and keep track of their accounts of a wide variety of formal objects of thought.
Let us look at a few simple examples of generating functions, much as I encountered them during my own first adventures in the Fair Land Of Combinatoria.
Suppose that we are given a set of three elements, say, \(\{ a, b, c \},\!\) and we are asked to find all the ways of choosing a subset from this collection.
We can represent this problem setup as the problem of computing the following product:
| \((1 + a)(1 + b)(1 + c).\!\) |
The factor \((1 + a)\!\) represents the option that we have, in choosing a subset of \(\{ a, b, c \},\!\) to leave the element \(a\!\) out (signified by the \(1\!\)), or else to include it (signified by the \(a\!\)), and likewise for the other elements \(b\!\) and \(c\!\) in their turns.
Probably on account of all those years I flippered away playing the oldtime pinball machines, I tend to imagine a product like this being displayed in a vertical array:
|
\(\begin{matrix} (1 ~+~ a) \\ (1 ~+~ b) \\ (1 ~+~ c) \end{matrix}\) |
I picture this as a playboard with six bumpers, the ball chuting down the board in such a career that it strikes exactly one of the two bumpers on each and every one of the three levels.
So a trajectory of the ball where it hits the \(a\!\) bumper on the 1st level, hits the \(1\!\) bumper on the 2nd level, hits the \(c\!\) bumper on the 3rd level, and then exits the board, represents a single term in the desired product and corresponds to the subset \(\{ a, c \}.\!\)
Multiplying out the product \((1 + a)(1 + b)(1 + c),\!\) one obtains:
|
\(\begin{array}{*{15}{c}} 1 & + & a & + & b & + & c & + & ab & + & ac & + & bc & + & abc. \end{array}\) |
And this informs us that the subsets of choice are:
|
\(\begin{matrix} \varnothing, & \{ a \}, & \{ b \}, & \{ c \}, & \{ a, b \}, & \{ a, c \}, & \{ b, c \}, & \{ a, b, c \}. \end{matrix}\) |
Selection 7
The Signs for Multiplication (cont.)
|
The associative principle does not hold in this counting of factors. Because it does not hold, these subjacent numbers are frequently inconvenient in practice, and I therefore use also another mode of showing where the correlate of a term is to be found. This is by means of the marks of reference, \(\dagger ~ \ddagger ~ \parallel ~ \S ~ \P\), which are placed subjacent to the relative term and before and above the correlate. Thus, giver of a horse to a lover of a woman may be written: |
| \(\mathfrak{g}_{\dagger\ddagger} \, ^\dagger\mathit{l}_\parallel \, ^\parallel\mathrm{w} \, ^\ddagger\mathrm{h}\) |
|
The asterisk I use exclusively to refer to the last correlate of the last relative of the algebraic term. Now, considering the order of multiplication to be: — a term, a correlate of it, a correlate of that correlate, etc. — there is no violation of the associative principle. The only violations of it in this mode of notation are that in thus passing from relative to correlate, we skip about among the factors in an irregular manner, and that we cannot substitute in such an expression as \(\mathfrak{g}\mathit{o}\mathrm{h}\) a single letter for \(\mathit{o}\mathrm{h}.\!\) I would suggest that such a notation may be found useful in treating other cases of non-associative multiplication. By comparing this with what was said above [in CP 3.55] concerning functional multiplication, it appears that multiplication by a conjugative term is functional, and that the letter denoting such a term is a symbol of operation. I am therefore using two alphabets, the Greek and Kennerly, where only one was necessary. But it is convenient to use both. (Peirce, CP 3.71–72). |
Comment : Proto-Graphical Syntax
It is clear from our last excerpt that Peirce is already on the verge of a graphical syntax for the logic of relatives. Indeed, it seems likely that he had already reached this point in his own thinking.
For instance, it seems quite impossible to read his last variation on the theme of a “giver of a horse to a lover of a woman” without drawing lines of identity to connect up the corresponding marks of reference, like this:
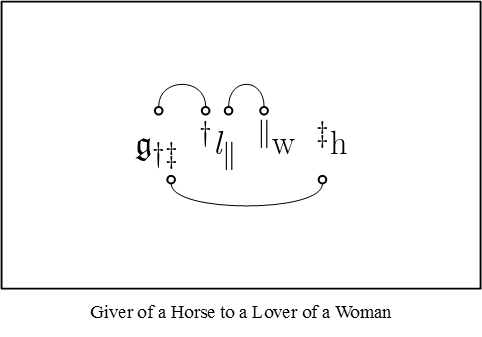 |
(3) |
Selection 8
The Signs for Multiplication (cont.)
|
Thus far, we have considered the multiplication of relative terms only. Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives. Now the absolute term “man” is really exactly equivalent to the relative term “man that is ——”, and so with any other. I shall write a comma after any absolute term to show that it is so regarded as a relative term. Then “man that is black” will be written: |
| \(\mathrm{m},\!\mathrm{b}\!\) |
|
But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one. Then: |
| \(\mathit{l},\!\mathit{s}\mathrm{w}\) |
|
will denote a lover of a woman that is a servant of that woman. The comma here after \(\mathit{l}\!\) should not be considered as altering at all the meaning of \(\mathit{l}\!\), but as only a subjacent sign, serving to alter the arrangement of the correlates. In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates. So: |
| \(\mathrm{m},\!,\!\mathrm{b},\!\mathrm{r}\) |
|
interpreted like |
| \(\mathfrak{g}\mathit{o}\mathrm{h}\) |
|
means a man that is a rich individual and is a black that is that rich individual. But this has no other meaning than: |
| \(\mathrm{m},\!\mathrm{b},\!\mathrm{r}\) |
|
or a man that is a black that is rich. Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number. If, therefore, \(\mathit{l},\!,\!\mathit{s}\mathrm{w}\) is not the same as \(\mathit{l},\!\mathit{s}\mathrm{w}\) (as it plainly is not, because the latter means a lover and servant of a woman, and the former a lover of and servant of and same as a woman), this is simply because the writing of the comma alters the arrangement of the correlates. And if we are to suppose that absolute terms are multipliers at all (as mathematical generality demands that we should}, we must regard every term as being a relative requiring an infinite number of correlates to its virtual infinite series “that is —— and is —— and is —— etc.” Now a relative formed by a comma of course receives its subjacent numbers like any relative, but the question is, What are to be the implied subjacent numbers for these implied correlates? Any term may be regarded as having an infinite number of factors, those at the end being ones, thus: |
| \(\mathit{l},\!\mathit{s}\mathrm{w} ~=~ \mathit{l},\!\mathit{s}\mathit{w},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1}, ~\text{etc.}\) |
|
A subjacent number may therefore be as great as we please. But all these ones denote the same identical individual denoted by \(\mathrm{w}\!\); what then can be the subjacent numbers to be applied to \(\mathit{s}\!\), for instance, on account of its infinite “that is”'s? What numbers can separate it from being identical with \(\mathrm{w}\!\)? There are only two. The first is zero, which plainly neutralizes a comma completely, since |
| \(\mathit{s},_0\!\mathrm{w} ~=~ \mathit{s}\mathrm{w}\) |
|
and the other is infinity; for as \(1^\infty\) is indeterminate in ordinary algbra, so it will be shown hereafter to be here, so that to remove the correlate by the product of an infinite series of ones is to leave it indeterminate. Accordingly, |
| \(\mathrm{m},_\infty\) |
|
should be regarded as expressing some man. Any term, then, is properly to be regarded as having an infinite number of commas, all or some of which are neutralized by zeros. “Something” may then be expressed by: |
| \(\mathit{1}_\infty\!\) |
|
I shall for brevity frequently express this by an antique figure one \((\mathfrak{1}).\) “Anything” by: |
| \(\mathit{1}_0\!\) |
|
I shall often also write a straight \(1\!\) for anything. (Peirce, CP 3.73). |
Commentary Work Area
Commentary Note 12.2
a b c d e f g h i o o o o o o o o o X | | : | : | | | 0 1 0 1 W, | | : | : | o o o o + - + + o X \ | / : : | | \ | / 0 0 1 1 L \|/ : : | | o o o o o o o o o X a b c d e f g h i |
a b c d e f g h i o o o o o o o o o X / \ : | : | / \ 0 1 0 1 L / \ : | : | o o o o + - + + o X \ | / : : | | \ | / 0 0 1 1 S \|/ : : | | o o o o o o o o o X a b c d e f g h i |
Commentary Note 12.3
a b c d e f g h i
o o o o o o o o o X
| |
| | W,
| |
o o o o o o o o o X
\ \ / / \ | / \ \ / /
\ / / \ | / \ \ / L
\ / \ / \|/ \ / \ /
o o o o o o o o o X
a b c d e f g h i
|
Commentary Note 12.4
|
\(\begin{array}{*{15}{c}} X & = & \{ & a, & b, & c, & d, & e, & f, & g, & h, & i\ & \} \\[6pt] W & = & \{ & d, & f\ & \} \\[6pt] L & = & \{ & b\!:\!a, & b\!:\!c, & c\!:\!b, & c\!:\!d, & e\!:\!d, & e\!:\!e, & e\!:\!f, & g\!:\!f, & g\!:\!h, & h\!:\!g, & h\!:\!i & \} \\[6pt] S & = & \{ & b\!:\!a, & b\!:\!c, & d\!:\!c, & d\!:\!d, & d\!:\!e, & f\!:\!e, & f\!:\!f, & f\!:\!g, & h\!:\!g, & h\!:\!i\ & \} \end{array}\) |
a b c d e f g h i
o o o o o o o o o X
| |
| | W,
| |
o o o o o o o o o X
\ \ / / \ | / \ \ / /
\ / / \ | / \ \ / L
\ / \ / \|/ \ / \ /
o o o o o o o o o X
\ / \ | / \ | / \ /
\ / \ | / \ | / \ / S
\ / \|/ \|/ \ /
o o o o o o o o o X
a b c d e f g h i
|
a b c d e f g h i
o o o o o o o o o X
|
| (LW),
|
o o o o o o o o o X
\ / \ | / \ | / \ /
\ / \ | / \ | / \ / S
\ / \|/ \|/ \ /
o o o o o o o o o X
a b c d e f g h i
|
a b c d e f g h i
o o o o o o o o o X
| |
| | (S^(LW)),
| |
o o o o o o o o o X
a b c d e f g h i
|
a b c d e f g h i o o o o o o o o o X \ \ / / \ | / \ \ / / \ / / \ | / \ \ / L \ / \ / \|/ \ / \ / o o o o o o o o o X \ / \ | / \ | / \ / \ / \ | / \ | / \ / S \ / \|/ \|/ \ / o o o o o o o o o X a b c d e f g h i |
Commentary Note 12.5
|
\( (\mathsf{L} \mathsf{W})_x ~=~ \sum_{p \in X} \mathsf{L}_{xp} \mathsf{W}_p \) |
|
\( (\mathsf{L} \mathsf{W})_q ~=~ \sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p \) |
|
\((\mathsf{L}^\mathsf{W})_x ~=~ \prod_{p \in X} \mathsf{L}_{xp}^{\mathsf{W}_p} \) |
|
\( (\mathsf{S}^\mathsf{L})_{xy} ~=~ \prod_{p \in X} \mathsf{S}_{xp}^{\mathsf{L}_{py}} \) |
|
\( (\mathsf{S}^\mathsf{L})_{xp} ~=~ \prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}} \) |
|
\( ((\mathsf{S}^\mathsf{L})^\mathsf{W})_x ~=~ (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x \) |
|
\( ((\mathsf{S}^\mathsf{L})^\mathsf{W})_x ~=~ \prod_{p \in X} (\mathsf{S}^\mathsf{L})_{xp}^{\mathsf{W}_p} ~=~ \prod_{p \in X} (\prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}})^{\mathsf{W}_p} ~=~ \prod_{p \in X} \prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}\mathsf{W}_p} \) |
|
\( (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x ~=~ \prod_{q \in X} \mathsf{S}_{xq}^{(\mathsf{L}\mathsf{W})_q} ~=~ \prod_{q \in X} \mathsf{S}_{xq}^{\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p} ~=~ \prod_{q \in X} \prod_{p \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp} \mathsf{W}_p} \) |
Commentary Note 12.6
Need a comment about the meaning of the sum \(\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p\!\) in the following equation:
|
\( (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x ~=~ \prod_{q \in X} \mathsf{S}_{xq}^{(\mathsf{L}\mathsf{W})_q} ~=~ \prod_{q \in X} \mathsf{S}_{xq}^{\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p} ~=~ \prod_{q \in X} \prod_{p \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp} \mathsf{W}_p}\! \) |
| \((\mathsf{L}\mathsf{W})_q ~=~ \sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p\!\) |
| \((\mathsf{L}\mathsf{W})_x ~=~ \sum_{p \in X} \mathsf{L}_{xp} \mathsf{W}_p\!\) |
| \(\mathrm{w} ~=~ \sum_{x \in X} \mathsf{W}_x x \quad ?\!\) |
| \(\mathrm{w} ~=~ \sum_\mathbf{1} \mathrm{w}_\mathrm{X} \mathrm{X} \quad ?\!\) |
Commentary Note 12.7
- Problem about the relation of logical involution to the function space \(Y^X = \{ f : X \to Y \}.\)
- Notice that a function \(f : X \to Y\) is a "\(Y\!\)-evaluator of every \(X,\!\) or a "giver of a \(Y\!\)-value to every element of \(X\!\)".
Commentary on Selection 12 : Old Notes
|
Then |
| \((\mathit{s}^\mathit{l})^\mathrm{w}\!\) |
|
will denote whatever stands to every woman in the relation of servant of every lover of hers; and |
| \(\mathit{s}^{(\mathit{l}\mathrm{w})}\!\) |
|
will denote whatever is a servant of everything that is lover of a woman. So that |
| \((\mathit{s}^\mathit{l})^\mathrm{w} ~=~ \mathit{s}^{(\mathit{l}\mathrm{w})}.\) |
|
(Peirce, CP 3.77). |
Then we have the following results:
| \(\mathit{s}^{(\mathit{l}\mathrm{w})}\!\) | \(=\!\) | \(\bigcap_{x \in LW} \operatorname{proj}_1 (S \star x)\) | ||
| \((\mathit{s}^\mathit{l})^\mathrm{w}\!\) | \(=\!\) | \(\bigcap_{x \in W} \operatorname{proj}_1 (S^L \star x) \quad ???\) |
But what is \(S^L \quad ???\)
Suppose we try this:
| \(S^L ~=~ \bigcap_{x \in \operatorname{proj}_1 L} \operatorname{proj}_1 (S \star x)\!\) |
No, it looks like I need to think about this some more …
a b c d e f g h i o o o o o o o o o X / \ : | : | / \ 0 1 0 1 L / \ : | : | o o o o + - + + o X \ | / : : | | \ | / 0 0 1 1 S \|/ : : | | o o o o o o o o o X a b c d e f g h i |
It looks like there is a "servant of every lover of" link between \(i\!\) and \(j\!\) if and only if \(i \cdot S ~\supseteq~ L \cdot j.\) But the vacuous inclusions will make this non-intuitive.
Recall the analogy between involution and implication:
|
\( \begin{bmatrix} 0^0 & = & 1 \\ 0^1 & = & 0 \\ 1^0 & = & 1 \\ 1^1 & = & 1 \end{bmatrix} \qquad\qquad\qquad \begin{bmatrix} 0\!\Leftarrow\!0 & = & 1 \\ 0\!\Leftarrow\!1 & = & 0 \\ 1\!\Leftarrow\!0 & = & 1 \\ 1\!\Leftarrow\!1 & = & 1 \end{bmatrix} \) |
So it begins to look like this:
| \((\mathsf{S}^\mathsf{L})_{ab} ~=~ \prod_{x \in X} \mathsf{S}_{ax}^{\mathsf{L}_{xb}}\!\) |
In other words, \((\mathsf{S}^\mathsf{L})_{ab} = 0\!\) if and only if there exists an \(x \in X\!\) such that \(\mathsf{S}_{ax} = 0\!\) and \(\mathsf{L}_{xb} = 1.\!\)
Commentary on Selection 12 : Older Notes
The logic of terms is something of a lost art these days, when the current thinking in logic tends to treat the complete proposition as the quantum of discourse, ne plus infra. With absolute terms, or monadic relatives, and the simpler operations on dyadic relatives, the necessary translations between propositions and terms are obvious enough, but now that we've reached the threshold of higher adic relatives and operations as complex as exponentiation, it is useful to stop and consider the links between these two languages.
The term exponentiation is more generally used in mathematics for operations that involve taking a base to a power, and is slightly preferable to involution since the latter is used for different concepts in different contexts. Operations analogous to taking powers are widespread throughout mathematics and Peirce frequently makes use of them in a number of important applications, for example, in his theory of information. But that's another story.
The function space \(Y^X,\!\) where \(X\!\) and \(Y\!\) are sets, is the set of all functions from \(X\!\) to \(Y.\!\) An alternative notation for \(Y^X\!\) is \((X \to Y).\!\) Thus we have the following equivalents:
| \(\begin{matrix}Y^X & = & (X \to Y) & = & \{ f : X \to Y \}\end{matrix}\!\) |
If \(X\!\) and \(Y\!\) have cardinalities \(|X|\!\) and \(|Y|,\!\) respectively, then the function space \(Y^X\!\) has a cardinality given by the following equation:
| \(\begin{matrix}|Y^X| & = & |Y|^{|X|}\end{matrix}\!\) |
In the special case where \(Y = \mathbb{B} = \{ 0, 1 \},\!\) the function space \(\mathbb{B}^X\!\) is the set of functions \(\{ f : X \to \mathbb{B} \}.\!\) If the elements \(0, 1 \in \mathbb{B}\!\) are interpreted as the logical values \(\mathrm{false}, \mathrm{true},\!\) respectively, then a function of the type \(X \to \mathbb{B}\!\) may be interpreted as a proposition about the elements in \(X.\!\)
Really Old Commentary Notes
Up to this point in the discussion, we have observed that
the "number of" map 'v' : S -> R such that 'v's = [s] has
the following morphic properties:
0. [0] = 0
1. 'v'
2. x -< y => [x] =< [y]
3. [x +, y] =< [x] + [y]
contingent:
4. [xy] = [x][y]
view relation P c X x Y x Z as related to three functions:
`p_1` c
`p_3` c X x Y x Pow(Z)
f(x)
f(x+y) = f(x) + f(y)
f(p(x, y)) = q(f(x), f(y))
P(x, y, z)
(f^-1)(y)
f(z(x, y)) = z'(f(x), f(y))
Definition. f(x:y:z) = (fx:fy:fz).
f(x:y:z) = (fx:fy:
x:y:z in R => fx:fy:fz in fR
R(x, y, z) => (fR)(fx, fy, fz)
(L, x, y, z) => (fL, fx, fy, fz)
(x, y, z, L) => (xf, yf, zf, Lf)
(x, y, z, b) => (xf, yf, zf, bf)
fzxy = z'(fx)(fy)
F
o
|
o
/ \
o o
o
. | .
. | .
. | .
. o .
. / \ .
. / \ .
. / \ .
. o o .
. . .
. . .
.
C o . / \ . o
| . / \ . | CF
| . o o . |
f o . . . o fF
/ \ . . . / \
/ . \ . o o
X o o Y XF YF
<u, v, w> in P ->
o---------o---------o---------o---------o
| # h | h | f |
o=========o=========o=========o=========o
| P # X | Y | Z |
o---------o---------o---------o---------o
| Q # U | V | W |
o---------o---------o---------o---------o
Products of diagonal extensions:
1,1, = !1!!1!
= "anything that is anything that is ---"
= "anything that is ---"
= !1!
m,n = "man that is noble"
= (C:C +, I:I +, J:J +, O:O)(C +, D +, O)
= C +, O
n,m = "noble that is man"
= (C:C +, D:D +, O:O)(C +, I +, J +, O)
= C +, O
n,w = "noble that is woman"
= (C:C +, D:D +, O:O)(B +, D +, E)
= D
w,n = "woman that is noble"
= (B:B +, D:D +, E:E)(C +, D +, O)
= D
Given a set X and a subset M c X, define e_M,
the "idempotent representation" of M over X,
as the 2-adic relation e_M c X x X which is
the identity relation on M. In other words,
e_M = {<x, x> : x in M}.
Transposing this by steps into Peirce's notation:
e_M = {<x, x> : x in M}
= {x:x : x in M}
= Sum_X |x in M| x:x
'l' = "lover of ---"
's' = "servant of ---"
'l', = "lover that is --- of ---"
's', = "servant that is --- of ---"
| But not only may any absolute term be thus regarded as a relative term,
| but any relative term may in the same way be regarded as a relative with
| one correlate more. It is convenient to take this additional correlate
| as the first one.
|
| Then:
|
| 'l','s'w
|
| will denote a lover of a woman that is a servant of that woman.
|
| C.S. Peirce, CP 3.73
o---------o----+----o---------o---------o----+----o---------o
o-----------------------------o-----------------------------o
| Objective Framework (OF) | Interpretive Framework (IF) |
o-----------------------------o-----------------------------o
| Objects | Signs |
o-----------------------------o-----------------------------o
| |
| C o--------------- |
| |
| F o--------------- |
| |
| I o--------------- |
| |
| O o--------------- |
| |
| B o--------------- |
| |
| D o--------------- |
| |
| E o--------------- |
| o "m" |
| / |
| / |
| / |
| o o o-----------@ |
| \ |
| \ |
| \ |
| o |
| |
o-----------------------------o-----------------------------o
†‡||§¶
@#||$%
quality, reflection, synecdoche
1. neglect of
2. neglect of
3. neglect of nil?
Now, it's not the end of the story, of course, but it's a start.
The significant thing is what is usually the significant thing
in mathematics, at least, that two distinct descriptions refer
to the same things. Incidentally, Peirce is not really being
as indifferent to the distinctions between signs and things
as this ascii text makes him look, but uses a host of other
type-faces to distinguish the types and the uses of signs.
Discussion Notes
Discussion Note 1
- Gary Richmond
- I wonder if the necessary “elementary triad” spoken of below isn't somehow implicated in those discussions “invoking a closure principle”.
- C.S. Peirce
- CP 1.292. It can further be said in advance, not, indeed, purely a priori but with the degree of apriority that is proper to logic, namely, as a necessary deduction from the fact that there are signs, that there must be an elementary triad. For were every element of the phaneron a monad or a dyad, without the relative of teridentity (which is, of course, a triad), it is evident that no triad could ever be built up. Now the relation of every sign to its object and interpretant is plainly a triad. A triad might be built up of pentads or of any higher perissad elements in many ways. But it can be proved — and really with extreme simplicity, though the statement of the general proof is confusing — that no element can have a higher valency than three.
- Gary Richmond
- (Of course this passage also directly relates to the recent thread on Identity and Teridentity.)
- Jon Awbrey
- Yes, generally speaking, I think that there are deep formal principles here that manifest themselves in these various guises: the levels of intention or the orders of reflection, the sign relation, pragmatic conceivability, the generative sufficiency of 3-adic relations for all practical intents, and the irreducibility of continuous relations. I have run into themes in combinatorics, group theory, and Lie algebras that are tantalizingly reminiscent of the things that Peirce says here, but it will take me some time to investigate them far enough to see what's going on.
- Gary Richmond
- PS. I came upon the above passage last night reading through the Peirce selections in John J. Stuhr's Classical American Philosophy : Essential Readings and Interpretive Essays, Oxford University, 1987 (the passage above is found on pp. 61–62), readily available in paperback in a new edition, I believe.
- An aside: These excerpts in Sturh include versions of a fascinating “Intellectual Autobiography”, Peirce's summary of his scientific, especially, philosophic accomplishments. I've seen them published nowhere else.
Discussion Note 2
- Benjamin Udell
- I'm in the process of moving back to NYC and have had little opportunity to do more than glance through posts during the past few weeks, but this struck me because it sounds something I really would like to know about, but I didn't understand it:
- Jon Awbrey
- Notice that Peirce follows the mathematician's usual practice, then and now, of making the status of being an "individual" or a "universal" relative to a discourse in progress. I have come to appreciate more and more of late how radically different this "patchwork" or "piecewise" approach to things is from the way of some philosophers who seem to be content with nothing less than many worlds domination, which means that they are never content and rarely get started toward the solution of any real problem. Just my observation, I hope you understand.
- Benjamin Udell
- "Many worlds domination", "nothing less than many worlds domination" -- as opposed to the patchwork or piecewise approach. What is many worlds domination? When I hear "many worlds" I think of Everett's Many Worlds interpretation of quantum mechanics.
- Jon Awbrey
- Yes, it is a resonance of Edward, Everett, and All the Other Whos in Whoville, but that whole microcosm is itself but the frumious reverberation of Leibniz's Maenadolatry. More sequitur, though, this is an issue that has simmered beneath the surface of my consciousness for several decades now and only periodically percolates itself over the hyper-critical thrashold of expression. Let me see if I can a better job of it this time. The topic is itself a patchwork of infernally recurrent patterns. Here are a few pieces of it that I can remember arising recently:
|
Zeroth Law Of Semantics |
- A less catchy way of saying "meaning is a privilege not a right" would most likely be "meaning is a contingency not a necessity". But if I reflect on that phrase, it does not quite satisfy me, since a deeper lying truth is that contingency and necessity, connections in fact and connections beyond the reach of fact, depend on a line of distinction that is itself drawn on the scene of observation from the embodied, material, physical, non-point massive, non-purely-spectrelative point of view of an agent or community of interpretation, a discursive universe, an engauged interpretant, a frame of at least partial self-reverence, a hermeneutics in progress, or a participant observer. In short, this distinction between the contingent and the necessary is itself contingent, which means, among other things, that signs are always indexical at some least quantum.
Discussion Note 3
- Joe Ransdell
- Would the Kripke conception of the "rigid designator" be an instance of the "many worlds domination"? I was struck by your speaking of the "patchwork or piecewise" approach as well in that it seemed to me you might be expressing the same general idea that I have usually thought of in terms of contextualism instead: I mean the limits it puts upon what you can say a priori if you really take contextualism seriously, which is the same as recognizing indexicality as incapable of elimination, I think.
- Jon Awbrey
- Yes, I think this is the same ballpark of topics. I can't really speak for what Kripke had in mind, but I have a practical acquaintance with the way that some people have been trying to put notions like this to work on the applied ontology scene, and it strikes me as a lot of nonsense. I love a good parallel worlds story as much as anybody, but it strikes me that many worlds philosophers have the least imagination of anybody as to what an alternative universe might really be like and so I prefer to read more creative writers when it comes to that. But serially, folks, I think that the reason why some people evidently feel the need for such outlandish schemes — and the vast majority of the literature on counterfactual conditionals falls into the same spaceboat as this — is simply that they have failed to absorb, through the fault of Principian filters, a quality that Peirce's logic is thoroughly steeped in, namely, the functional interpretation of logical terms, that is, as signs referring to patterns of contingencies. It is why he speaks more often, and certainly more sensibly and to greater effect, of “conditional generals” than of “modal subjunctives”. This is also bound up with that element of sensibility that got lost in the transition from Peircean to Fregean quantifiers. Peirce's apriorities are always hedged with risky bets.
Discussion Note 4
- Benjamin Udell
- I wish I had more time to ponder the "many-worlds" issue (& that my books were not currently disappearing into heavily taped boxes). I had thought of the piecemeal approach's opposite as the attempt to build a kind of monolithic picture, e.g., to worry that there is not an infinite number of particles in the physical universe for the infinity integers. But maybe the business with rigid designators & domination of many worlds has somehow to do with monolithism.
- Jon Awbrey
- Yes, that's another way of saying it. When I look to my own priorities, my big worry is that logic as a discipline is not fulfilling its promise. I have worked in too many settings where the qualitative researchers and the quantitative researchers could barely even talk to one an Other with any understanding, and this I recognized as a big block to inquiry since our first notice of salient facts and significant phenomena is usually in logical, natural language, or qualitative forms, while our eventual success in resolving anomalies and solving practical problems depends on our ability to formalize, operationalize, and quantify the issues, even if only to a very partial degree, as it generally turns out.
- When I look to the history of how logic has been deployed in mathematics, and through those media in science generally, it seems to me that the Piece Train started to go off track with the Principia Mathematica. All pokes in the rib aside, however, I tend to regard this event more as the symptom of a localized cultural phenomenon than as the root cause of the broader malaise.
Discussion Note 5
- C.S. Peirce
| For example, |
| \(\mathrm{f} + \mathrm{u}\!\) |
| means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are besides themselves. |
- Clark Goble
- Could you clarify your use of “besides”?
- I think I am following your thinking in that you don't want the logical terms to be considered to have any necessary identity between them. Is that right?
- Jon Awbrey
- I use vertical sidebars "|" for long quotations, so this is me quoting Peirce at CP 3.67 who is explaining in an idiomatic way Boole's use of the plus sign for a logical operation that is strictly speaking limited to terms for mutually exclusive classes. The operation would normally be extended to signify the “symmetric difference” operator. But Peirce is saying that he prefers to use the sign \({}^{\backprime\backprime} +\!\!, {}^{\prime\prime}\) for inclusive disjunction, corresponding to the union of the associated classes. Peirce calls Boole's operation “invertible” because it amounts to the sum operation in a field, whereas the inclusive disjunction or union is “non-invertible”, since knowing that \(A \cup B = C\!\) does not allow one to say determinately that \(A = C - B.\!\) I can't recall if Boole uses this “besides” idiom, but will check later.
Discussion Note 6
- Jon Awbrey
- I use vertical sidebars “|” for long quotations, so this is me quoting Peirce at CP 3.67 who is explaining in an idiomatic way Boole's use of the plus sign for a logical operation that is strictly speaking limited to terms for mutually exclusive classes.
- Clark Goble
- Is that essay related to any of the essays in the two volume Essential Peirce? I'm rather interested in how he speaks there.
- Jon Awbrey
- No, the EP volumes are extremely weak on logical selections. I see nothing there that deals with the logic of relatives.
- But Peirce is saying that he prefers to use the sign \({}^{\backprime\backprime} +\!\!, {}^{\prime\prime}\) for inclusive disjunction, corresponding to the union of the associated classes.
- Clark Goble
- The reason I asked was more because it seemed somewhat interesting in light of the logic of operators in quantum mechanics. I was curious if the use of “beside” might relate to that. But from what you say it probably was just me reading too much into the quote. The issue of significance was whether the operation entailed the necessity of mutual exclusivity or whether some relationship between the classes might be possible. I kind of latched on to Peirce's odd statement about “all French violinists are beside themselves”.
- Did Peirce have anything to say about what we'd call non-commuting operators?
- Jon Awbrey
- In general, 2-adic relative terms are non-commutative. For example, a brother of a mother is not identical to a mother of a brother.
Discussion Note 7
- Gary Richmond
- I am very much enjoying, which is to say, learning from your interlacing commentary on Peirce's 1870 “Logic of Relatives” paper.
- What an extraordinary paper the 1870 “LOR” is! Your notes helped me appreciate the importance of the unanticipated proposal of P's to “assign to all logical terms, numbers”. On the other hand, the excerpts suggested to we why Peirce finally framed his Logic of Relatives into graphical form. Still, I think that a thorough examination of the 1970 paper might serve as propaedeutic (and of course, much more) for the study of the alpha and beta graphs.
- Jon Awbrey
- Yes, there's gold in them thar early logic papers that has been “panned” but nowhere near mined in depth yet. The whole quiver of arrows between terms and numbers harks back to the numeri characteristici of Leibniz, of course, but Leibniz attended more on the intensional chains of being while Peirce will here start to “escavate” the extensional hierarchies.
- I consider myself rewarded that you see the incipient impulse toward logical graphs, as one of the most striking things to me about this paper is to see these precursory seeds already planted here within it and yet to know how long it will take them to sprout and bloom.
- Peirce is obviously struggling to stay within the linotyper's art — a thing that we, for all our exorbitant hype about markable text, are still curiously saddled with — but I do not believe that it is possible for any mind equipped with a geometrical imagination to entertain these schemes for connecting up terminological hubs with their terminological terminals without perforce stretching imaginary strings between the imaginary gumdrops.
- Gary Richmond
- I must say though that the pace at which you've been throwing this at us is not to be kept up with by anyone I know “in person or by reputation”. I took notes on the first 5 or 6 Notes, but can now just barely find time to read through your posts.
- Jon Awbrey
- Oh, I was trying to burrow as fast as I could toward the more untapped veins — I am guessing that things will probably “descalate” a bit over the next week, but then, so will our attention spans …
- Speaking of which, I will have to break here, and pick up the rest later …
Discussion Note 8
- Gary Richmond
- In any event, I wish that you'd comment on Note 5 more directly (though you do obliquely in your own diagramming of “every [US] Vice-President(s) … [who is] every President(s) of the US Senate”.
- Jon Awbrey
- There are several layers of things to say about that, and I think that it would be better to illustrate the issues by way of the examples that Peirce will soon be getting to, but I will see what I can speak to for now.
- Gary Richmond
- But what interested me even more in LOR, Note 5, was the sign \({}^{\backprime\backprime} < {}^{\prime\prime}\!\) (“less than” joined to the sign of identity \({}^{\backprime\backprime} = {}^{\prime\prime}\!\) to yield Peirce's famous sign \({}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!\) (or more clearly, \({}^{\backprime\backprime} \texttt{=}\!\texttt{<} {}^{\prime\prime}\!\)) of inference, which combines the two (so that \({}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!\) (literally, “as small as”) means “is”. I must say I both “get” this and don't quite (Peirce's example(s) of the frenchman helped a little). Perhaps your considerably more mathematical mind can help clarify this for a non-mathematician such as myself. (My sense is that “as small as” narrows the terms so that “everything that occurs in the conclusion is already contained in the premise”.) I hope I'm not being obtuse here. I'm sure it's “all too simple for words”.
- Jon Awbrey
- Then let us draw a picture.
- The proposition \(\texttt{(} F ~ \texttt{(} G \texttt{))},\!\) read as \({}^{\backprime\backprime} \mathrm{not}~ F ~\mathrm{without}~ G {}^{\prime\prime},\!\) states that the region indicated by \(F ~ \texttt{(} G \texttt{)},\!\) in other words, where \(F ~\mathrm{and~not}~ G\!\) holds true, is the only region exempted from the occupation of being in this universe:
o-----------------------------------------------------------o |`X`````````````````````````````````````````````````````````| |```````````````````````````````````````````````````````````| |`````````````o-------------o```o-------------o`````````````| |````````````/ \`/```````````````\````````````| |```````````/ o`````````````````\```````````| |``````````/ /`\`````````````````\``````````| |`````````/ /```\`````````````````\`````````| |````````/ /`````\`````````````````\````````| |```````o o```````o`````````````````o```````| |```````| |```````|`````````````````|```````| |```````| |```````|`````````````````|```````| |```````| F |```````|````````G````````|```````| |```````| |```````|`````````````````|```````| |```````| |```````|`````````````````|```````| |```````o o```````o`````````````````o```````| |````````\ \`````/`````````````````/````````| |`````````\ \```/`````````````````/`````````| |``````````\ \`/`````````````````/``````````| |```````````\ o`````````````````/```````````| |````````````\ /`\```````````````/````````````| |`````````````o-------------o```o-------------o`````````````| |```````````````````````````````````````````````````````````| |```````````````````````````````````````````````````````````| o-----------------------------------------------------------o |
- Collapsing the vacuous region like soapfilm popping on a wire frame, we draw the constraint \(\texttt{(} F ~ \texttt{(} G \texttt{))}\!\) in the following alternative fashion:
o-----------------------------------------------------------o |`X`````````````````````````````````````````````````````````| |```````````````````````````````````````````````````````````| |```````````````````````````````o-------------o`````````````| |``````````````````````````````/```````````````\````````````| |`````````````````````````````o`````````````````\```````````| |````````````````````````````/`\`````````````````\``````````| |```````````````````````````/```\`````````````````\`````````| |``````````````````````````/`````\`````````````````\````````| |`````````````````````````o```````o`````````````````o```````| |`````````````````````````|```````|`````````````````|```````| |`````````````````````````|```````|`````````````````|```````| |`````````````````````````|```F```|````````G````````|```````| |`````````````````````````|```````|`````````````````|```````| |`````````````````````````|```````|`````````````````|```````| |`````````````````````````o```````o`````````````````o```````| |``````````````````````````\`````/`````````````````/````````| |```````````````````````````\```/`````````````````/`````````| |````````````````````````````\`/`````````````````/``````````| |`````````````````````````````o`````````````````/```````````| |``````````````````````````````\```````````````/````````````| |```````````````````````````````o-------------o`````````````| |```````````````````````````````````````````````````````````| |```````````````````````````````````````````````````````````| o-----------------------------------------------------------o |
- So all of the following expressions, under suitable mutations of interpretation, are just so many ways of saying that the denotation of \({}^{\backprime\backprime} F {}^{\prime\prime}\!\) is contained within the denotation of \({}^{\backprime\backprime} G {}^{\prime\prime}.\!\)
|
\(\begin{array}{l} \texttt{(} F ~ \texttt{(} G \texttt{))} \\[4pt] F \Rightarrow G \\[4pt] F ~\texttt{=}\!\texttt{<}~ G \\[4pt] F ~\texttt{-}\!\texttt{<}~ G \\[4pt] F \subseteq G \end{array}\!\) |
- Let us now look to the “characteristic functions” or “indicator functions” of the various regions of being. It is frequently convenient to use the same letters for them and merely to keep a variant interpretation “en-thy-meme”, but let us be more meticulous here, and reserve the corresponding lower case letters \(f\!\) and \(g\!\) to denote the indicator functions of the regions \(F\!\) and \(G,\!\) respectively.
- Taking \(\mathbb{B} = \{ 0, 1 \}~\!\) as the boolean domain, we have:
|
\(\begin{array}{lcl} f, g : X & \to & \mathbb{B} \\[4pt] f^{-1}(1) & = & F \\[4pt] g^{-1}(1) & = & G \end{array}\!\) |
- In general, for a proposition \(h : X \to \mathbb{B},\!\) an expression like \(h^{-1}(1)\!\) can be read as “the inverse of \(h\!\) evaluated at \(1\!\)”, in effect, denoting the set of points in \(X\!\) where \(h\!\) evaluates to \(\mathrm{true}.\!\) This is called the “fiber of truth” under \(h,\!\) and I have gotten where I like to abbreviate it as \([|h|].\!\)
- Accordingly, we have:
|
\(\begin{array}{*{7}{l}} F & = & [|f|] & = & f^{-1}(1) & \subseteq & X \\[4pt] G & = & [|g|] & = & g^{-1}(1) & \subseteq & X \end{array}\!\) |
- This brings us to the question, what sort of “functional equation” between \(f\!\) and \(g\!\) goes with the regional constraint \(\texttt{(} F ~ \texttt{(} G \texttt{))}\!\)?
- Just this, that \(f(x) ~\texttt{=}\!\texttt{<}~ g(x)\!\) for all \(x\!\) in \(X,\!\) where the \({}^{\backprime\backprime} \texttt{=}\!\texttt{<} {}^{\prime\prime}\!\) relation on the values in \(\mathbb{B}\!\) has the following operational table for the pairing \({}^{\backprime\backprime} \mathrm{row~head} ~\texttt{=}\!\texttt{<}~ \mathrm{column~head} {}^{\prime\prime}.\!\)
|
\(\begin{array}{|c||cc|} \hline \texttt{=}\!\texttt{<} & 0 & 1 \\ \hline\hline 0 & 1 & 1 \\ 1 & 0 & 1 \\ \hline \end{array}\!\) |
- And this, of course, is the same thing as the truth table for the conditional connective or the implication relation.
- Gary Richmond
- By the way, in the semiosis implied by the modal gamma graphs, could \({}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!\) (were it used there, which of course it is not) ever be taken to mean “leads to” or “becomes” or “evolves into”? I informally use it that way myself, using the ordinary arrow for implication.
- Jon Awbrey
- I am a bit insensitive to the need for modal logic, since necessity in mathematics always seems to come down to being a matter of truth for all actual cases, if under an expanded sense of actuality that makes it indiscernible from possibility, so I must beg off here. But there are places where Peirce makes a big deal about the advisability of drawing the \({}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!\) symbol in one fell stroke of the pen, kind of like a “lazy gamma” — an old texican cattle brand — and I have seen another place where he reads \(A ~\texttt{-}\!\texttt{<}~ B\!\) as \({}^{\backprime\backprime} A, ~\text{in every way that it can be, is}~ B {}^{\prime\prime},\!\) as if this \({}^{\backprime\backprime} \texttt{-}\!\texttt{<} {}^{\prime\prime}\!\) fork in the road led into a veritable garden of branching paths.
- And out again …
Discussion Note 9
- Jon Awbrey
- I am a bit insensitive to the need for modal logic, since necessity in mathematics always seems to come down to being a matter of truth for all actual cases, if under an expanded sense of actuality that makes it indiscernible from possibility, so I must beg off here.
- Gary Richmond
- I cannot agree with you regarding modal logic. Personally I feel that the gamma part of the EGs is of the greatest interest and potential importance, and as Jay Zeman has made clear in his dissertation, Peirce certainly thought this as well.
- Jon Awbrey
- You disagree that I am insensitive? Well, certainly nobody has ever done that before! No, I phrased it that way to emphasize the circumstance that it ever hardly comes up as an issue within the limited purview of my experience, and when it does — as in topo-logical boundary situations — it seems to require a sort of analysis that doesn't comport all that well with the classical modes and natural figures of speech about it. Then again, I spent thirty years trying to motorize Alpha, have only a few good clues how I would go about Beta, and so Gamma doesn't look like one of those items on my plate.
- Speeching Of Which ---
- Best Of The Season ...
- And Happy Trailing ...
Discussion Note 10
- Bernard Morand
- Thanks for your very informative talk. There is a point that I did not understand in Note 35:
- Jon Awbrey
- If we operate in accordance with Peirce's example of \(\mathfrak{g}\mathit{o}\mathrm{h}\) as the “giver of a horse to an owner of that horse”, then we may assume that the associative law and the distributive law are by default in force, allowing us to derive this equation:
|
\(\begin{array}{lll} \mathit{l},\!\mathit{s}\mathrm{w} & = & \mathit{l},\!\mathit{s}(\mathrm{B} ~~+\!\!,~~ \mathrm{D} ~~+\!\!,~~ \mathrm{E}) \\[6pt] & = & \mathit{l},\!\mathit{s}\mathrm{B} ~~+\!\!,~~ \mathit{l},\!\mathit{s}\mathrm{D} ~~+\!\!,~~ \mathit{l},\!\mathit{s}\mathrm{E} \end{array}\) |
- Bernard Morand
- May be because language or more probably my lack of training in logic, what does mean that “associative law and distributive law are by default in force”?
- Jon Awbrey
- Those were some tricky Peirces, and I was trying to dodge them as artful as could be, but now you have fastly apprehended me!
- It may be partly that I left out the initial sections of this paper where Peirce discusses how he will regard the ordinarily applicable principles in the process of trying to extend and generalize them (CP 3.45–62), but there may be also an ambiguity in Peirce's use of the phrase “absolute conditions” (CP 3.62–68). Does he mean “absolutely necessary”, “indispensable”, “inviolate”, or does he mean “the conditions applying to the logic of absolute terms”, in which latter case we would expect to alter them sooner or later?
- We lose the commutative law, \(xy = yx,\!\) as soon as we extend to 2-adic relations, but keep the associative law, \(x(yz) = (xy)z,\!\) as the multiplication of 2-adics is the logical analogue of ordinary matrix multiplication, and Peirce like most mathematicians treats the double distributive law, \(x(y + z) = xy + xz\!\) and \((x + y)z = xz + yz,\!\) and as something that must be striven to preserve as far as possible.
- Strictly speaking, Peirce is already using a principle that goes beyond the ordinary associative law, but that is recognizably analogous to it, for example, in the modified Othello case, where \((\mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{D})(\mathrm{J}\!:\!\mathrm{D})(\mathrm{D}) = \mathrm{J}.\!\)
- If it were strictly associative, then we would have the following:
|
\(\begin{array}{lcccc} (J:J:D)((J:D)(D)) & = & (J:J:D)(J) & = & 0? \\[4pt] ((J:J:D)(J:D))(D) & = & (J)(D) & = & 0? \end{array}\) |
- In other words, the intended relational linkage would be broken. However, the type of product that Peirce is taking for granted in this situation often occurs in mathematics in just this way. There is another location where he comments more fully on this, but I have the sense that it was a late retrospective remark, and I do not recall if it was in CP or in the microfilm MSs that I read it.
- By “default” conditions I am referring more or less to what Peirce says at the end of CP 3.69, where he use an argument based on the distributive principle to rationalize the idea that “A term multiplied by two relatives shows that the same individual is in the two relations.” This means, for example, that one can let \({}^{\backprime\backprime} \mathfrak{g}\mathit{o}\mathrm{h} {}^{\prime\prime}\!\), without subjacent marks or numbers, be interpreted on the default convention of “overlapping scopes”, where the two correlates of \(\mathfrak{g}\!\) are given by the next two terms in line, namely, \(\mathit{o}\!\) and \(\mathrm{h},\!\) and the single correlate of \(\mathit{o}\!\) is given by the very next term in line, namely, \(\mathrm{h}.\!\) Thus, it is only when this natural scoping cannot convey the intended sense that we have to use more explicit mark-up devices.
- Bernard Morand
- About another point: do you think that the LOR could be of some help to solve the puzzle of the “second way of dividing signs” where CSP concludes that 66 classes could be made out of the 10 divisions (Letters to lady Welby)? (As I see them, the ten divisions involve a mix of relative terms, dyadic relations, and a triadic one. In order to make 66 classes it is clear that these 10 divisions have to be stated under some linear order. The nature of this order is at the bottom of the disagreements on the subject).
- Jon Awbrey
- This topic requires a longer excuse from me than I am able to make right now, but maybe I'll get back to it later today or tomorrow.
Discussion Note 11
- Bernard Morand
- About another point: do you think that the LOR could be of some help to solve the puzzle of the "second way of dividing signs" where CSP concludes that 66 classes could be made out of the 10 divisions (Letters to lady Welby)? (As I see them, the ten divisions involve a mix of relative terms, dyadic relations and a triadic one. In order to make 66 classes it is clear that these 10 divisions have to be stated under some linear order. The nature of this order is at the bottom of the disagreements on the subject).
- Jon Awbrey
- Yes. At any rate, I have a pretty clear sense from reading Peirce's work in the period 1865–1870 that the need to understand the function of signs in scientific inquiry is one of the main reasons he found himself forced to develop both the theory of information and the logic of relatives.
- Peirce's work of this period is evenly distributed across the extensional and intensional pans of the balance in a way that is very difficult for us to follow anymore. I remember when I started looking into this I thought of myself as more of an "intensional, synthetic" than an "extensional, analytic" type of thinker, but that seems like a long time ago, as it soon became clear that much less work had been done in the Peirce community on the extensional side of things, while that was the very facet that needed to be polished up in order to reconnect logic with empirical research and mathematical models. So I fear that I must be content that other able people are working on the intensional classification of sign relations.
- Still, the way that you pose the question is very enticing, so maybe it is time for me to start thinking about this aspect of sign relations again, if you could say more about it.
Discussion Note 12
- Bernard Morand
- The pairing “intensional, synthetic” against the other “extensional, analytic” is not one that I would have thought so. I would have paired synthetic with extensional because synthesis consists in adding new facts to an already made conception. On the other side analysis looks to be the determination of features while neglecting facts. But may be there is something like a symmetry effect leading to the same view from two different points.
- Jon Awbrey
- Oh, it's not too important, as I don't put a lot of faith in such divisions, and the problem for me is always how to integrate the facets of the object, or the faculties of the mind — but there I go being synthetic again!
- I was only thinking of a conventional contrast that used to be drawn between different styles of thinking in mathematics, typically one points to Descartes, and the extensionality of analytic geometry, versus Desargues, and the intensionality of synthetic geometry.
- It may appear that one has side-stepped the issue of empiricism that way, but then all that stuff about the synthetic à priori raises its head, and we have Peirce's insight that mathematics is observational and even experimental, and so I must trail off into uncoordinated elliptical thoughts …
- The rest I have to work at a while, and maybe go back to the Welby letters.
Discussion Note 13
- Bernard Morand
- I will try to make clear the matter, at least as far as I understand it for now. We can summarize in a table the 10 divisions with their number in a first column, their title in current (peircean) language in the second and some kind of logical notation in the third. The sources come mainly from the letters to Lady Welby. While the titles come from CP 8.344, the third column comes from my own interpretation.
- So we get:
I - According to the Mode of Apprehension of the Sign itself - S
II - According to the Mode of Presentation of the Immediate Object - Oi
III - According to the Mode of Being of the Dynamical Object - Od
IV - According to the Relation of the Sign to its Dynamical Object - S-Od
V - According to the Mode of Presentation of the Immediate Interpretant - Ii
VI - According to the Mode of Being of the Dynamical Interpretant - Id
VII - According to the relation of the Sign to the Dynamical Interpretant - S-Id
VIII - According to the Nature of the Normal Interpretant - If
IX - According to the the relation of the Sign to the Normal Interpretant - S-If
X - According to the Triadic Relation of the Sign to its Dynamical Object
and to its Normal Interpretant - S-Od-If
|
- Jon Awbrey
- For my future study, I will reformat the table in a way that I can muse upon. I hope the roman numerals have not become canonical, as I cannot abide them.
Table. Ten Divisions of Signs (Peirce, Morand) o---o---------------o------------------o------------------o---------------o | | According To: | Of: | To: | | o===o===============o==================o==================o===============o | 1 | Apprehension | Sign Itself | | S | | 2 | Presentation | Immediate Object | | O_i | | 3 | Being | Dynamical Object | | O_d | | 4 | Relation | Sign | Dynamical Object | S : O_d | o---o---------------o------------------o------------------o---------------o | 5 | Presentation | Immediate Interp | | I_i | | 6 | Being | Dynamical Interp | | I_d | | 7 | Relation | Sign | Dynamical Interp | S : I_d | o---o---------------o------------------o------------------o---------------o | 8 | Nature | Normal Interp | | I_f | | 9 | Relation | Sign | Normal Interp | S : I_f | o---o---------------o------------------o------------------o---------------o | A | Relation | Sign | Dynamical Object | | | | | | & Normal Interp | S : O_d : I_f | o---o---------------o------------------o------------------o---------------o |
- Just as I have always feared, this classification mania appears to be communicable! But now I must definitely review the Welby correspondence, as all this stuff was a blur to my sensibilities the last 10 times I read it.
Discussion Note 14
- Jon Awbrey
Table. Ten Divisions of Signs (Peirce, Morand) o---o---------------o------------------o------------------o---------------o | | According To: | Of: | To: | | o===o===============o==================o==================o===============o | 1 | Apprehension | Sign Itself | | S | | 2 | Presentation | Immediate Object | | O_i | | 3 | Being | Dynamical Object | | O_d | | 4 | Relation | Sign | Dynamical Object | S : O_d | o---o---------------o------------------o------------------o---------------o | 5 | Presentation | Immediate Interp | | I_i | | 6 | Being | Dynamical Interp | | I_d | | 7 | Relation | Sign | Dynamical Interp | S : I_d | o---o---------------o------------------o------------------o---------------o | 8 | Nature | Normal Interp | | I_f | | 9 | Relation | Sign | Normal Interp | S : I_f | o---o---------------o------------------o------------------o---------------o | A | Relation | Sign | Dynamical Object | | | | | | & Normal Interp | S : O_d : I_f | o---o---------------o------------------o------------------o---------------o |
- Bernard Morand
- Yes this is clearer (in particular in expressing relations with “:”)
- Jon Awbrey
- This is what Peirce used to form elementary relatives, for example, \(o\!:\!s\!:\!i = (o, s, i),\!\) and I find it utterly ubertous in a wide variety of syntactic circumstances.
- Bernard Morand
- I suggest making a correction to myself if the table is destinate to become canonic.
- Jon Awbrey
- Hah! Good one!
- Bernard Morand
- I probably made a too quick jump from Normal Interpretant to Final Interpretant. As we know, the final interpretant, the ultimate one is not a sign for Peirce but a habit. So for the sake of things to come it would be more careful to retain \(\mathrm{I_n}\!\) in place of \(\mathrm{I_f}\!\) for now.
- Jon Awbrey
- This accords with my understanding of how the word is used in mathematics. In my own work it has been necessary to distinguish many different species of expressions along somewhat similar lines, for example: arbitrary, basic, canonical, decidable, normal, periodic, persistent, prototypical, recurrent, representative, stable, typical, and so on. So I will make the changes below:
Table. Ten Divisions of Signs (Peirce, Morand) o---o---------------o------------------o------------------o---------------o | | According To: | Of: | To: | | o===o===============o==================o==================o===============o | 1 | Apprehension | Sign Itself | | S | | 2 | Presentation | Immediate Object | | O_i | | 3 | Being | Dynamical Object | | O_d | | 4 | Relation | Sign | Dynamical Object | S : O_d | o---o---------------o------------------o------------------o---------------o | 5 | Presentation | Immediate Interp | | I_i | | 6 | Being | Dynamical Interp | | I_d | | 7 | Relation | Sign | Dynamical Interp | S : I_d | o---o---------------o------------------o------------------o---------------o | 8 | Nature | Normal Interp | | I_n | | 9 | Relation | Sign | Normal Interp | S : I_n | o---o---------------o------------------o------------------o---------------o | A | Tri. Relation | Sign | Dynamical Object | | | | | | & Normal Interp | S : O_d : I_n | o---o---------------o------------------o------------------o---------------o |
- Bernard Morand
- Peirce gives the following definition (CP 8.343).
- C.S. Peirce
- It is likewise requisite to distinguish the Immediate Interpretant, i.e. the Interpretant represented or signified in the Sign, from the Dynamic Interpretant, or effect actually produced on the mind by the Sign; and both of these from the Normal Interpretant, or effect that would be produced on the mind by the Sign after sufficient development of thought. (Collected Papers, CP 8.343).
- Jon Awbrey
- Well, you've really tossed me in the middle of the briar patch now! I must continue with my reading from the 1870 LOR, but now I have to add to my do-list the problems of comparing the whole variorum of letters and drafts of letters to Lady Welby. I have only the CP 8 and Wiener versions here, so I will depend on you for ample excerpts from the Lieb volume.
Discussion Note 15
- Jon Awbrey
- I will need to go back and pick up the broader contexts of your quotes. For ease of study I break Peirce's long paragraphs into smaller pieces.
- C.S. Peirce
|
It seems to me that one of the first useful steps toward a science of semeiotic (σημειωτική), or the cenoscopic science of signs, must be the accurate definition, or logical analysis, of the concepts of the science. I define a Sign as anything which on the one hand is so determined by an Object and on the other hand so determines an idea in a person's mind, that this latter determination, which I term the Interpretant of the sign, is thereby mediately determined by that Object. A sign, therefore, has a triadic relation to its Object and to its Interpretant. But it is necessary to distinguish the Immediate Object, or the Object as the Sign represents it, from the Dynamical Object, or really efficient but not immediately present Object. It is likewise requisite to distinguish the Immediate Interpretant, i.e. the Interpretant represented or signified in the Sign, from the Dynamic Interpretant, or effect actually produced on the mind by the Sign; and both of these from the Normal Interpretant, or effect that would be produced on the mind by the Sign after sufficient development of thought. On these considerations I base a recognition of ten respects in which Signs may be divided. I do not say that these divisions are enough. But since every one of them turns out to be a trichotomy, it follows that in order to decide what classes of signs result from them, I have 310, or 59049, difficult questions to carefully consider; and therefore I will not undertake to carry my systematical division of signs any further, but will leave that for future explorers. (Collected Papers, CP 8.343). |
- Jon Awbrey
- You never know when the future explorer will be yourself.
Discussion Note 16
Burks, the editor of CP 8, attaches this footnote to CP 8.342-379, "On the Classification of Signs": | From a partial draft of a letter to Lady Welby, bearing | the dates of 24, 25, and 28 December 1908, Widener IB3a, | with an added quotation in 368n23. ... There is a passage roughly comparable to CP 8.343 in a letter to Lady Welby dated 23 December 1908, pages 397-409 in Wiener, which is incidentally the notorious "sop to Cerberus" letter: | It is usual and proper to distinguish two Objects of a Sign, | the Mediate without, and the Immediate within the Sign. Its | Interpretant is all that the Sign conveys: acquaintance with | its Object must be gained by collateral experience. | | The Mediate Object is the Object outside of the Sign; I call | it the 'Dynamoid' Object. The Sign must indicate it by a hint; | and this hint, or its substance, is the 'Immediate' Object. | | Each of these two Objects may be said to be capable of either of | the three Modalities, though in the case of the Immediate Object, | this is not quite literally true. | | Accordingly, the Dynamoid Object may be a Possible; when I term | the Sign an 'Abstractive'; such as the word Beauty; and it will be | none the less an Abstractive if I speak of "the Beautiful", since it is | the ultimate reference, and not the grammatical form, that makes the sign | an 'Abstractive'. | | When the Dynamoid Object is an Occurrence (Existent thing or Actual fact | of past or future), I term the Sign a 'Concretive'; any one barometer | is an example; and so is a written narrative of any series of events. | | For a 'Sign' whose Dynamoid Object is a Necessitant, I have at present | no better designation than a 'Collective', which is not quite so bad a | name as it sounds to be until one studies the matter: but for a person, | like me, who thinks in quite a different system of symbols to words, it | is so awkward and often puzzling to translate one's thought into words! | | If the Immediate Object is a "Possible", that is, if the Dynamoid Object | is indicated (always more or less vaguely) by means of its Qualities, etc., | I call the Sign a 'Descriptive'; | | if the Immediate is an Occurrence, I call the Sign a 'Designative'; | | and if the Immediate Object is a Necessitant, I call the Sign a | 'Copulant'; for in that case the Object has to be so identified | by the Interpreter that the Sign may represent a necessitation. | My name is certainly a temporary expedient. | | It is evident that a possible can determine nothing but a Possible, | it is equally so that a Necessitant can be determined by nothing but | a Necessitant. Hence it follows from the Definition of a Sign that | since the Dynamoid Object determines the Immediate Object, | | Which determines the Sign itself, | which determines the Destinate Interpretant | which determines the Effective Interpretant | which determines the Explicit Interpretant | | the six trichotomies, instead of determining 729 classes of signs, | as they would if they were independent, only yield 28 classes; | and if, as I strongly opine (not to say almost prove), there | are four other trichotomies of signs of the same order of | importance, instead of making 59,049 classes, these will | only come to 66. | | The additional 4 trichotomies are undoubtedly, first: | | Icons*, Symbols, Indices, | |*(or Simulacra, Aristotle's 'homoiomata'), caught from Plato, who I guess took it | from the Mathematical school of logic, for it earliest appears in the 'Phaedrus' | which marks the beginning of Plato's being decisively influenced by that school. | Lutoslowski is right in saying that the 'Phaedrus' is later than the 'Republic' | but his date 379 B.C. is about eight years too early. | | and then 3 referring to the Interpretants. One of these I am pretty confident | is into: 'Suggestives', 'Imperatives', 'Indicatives', where the Imperatives | include the Interrogatives. Of the other two I 'think' that one must be | into Signs assuring their Interpretants by: | | Instinct, Experience, Form. | | The other I suppose to be what, in my 'Monist' | exposition of Existential Graphs, I called: | | Semes, Phemes, Delomes. | | CSP, 'Selected Writings', pp. 406-408. | |'Charles S. Peirce: Selected Writings (Values in a Universe of Chance)', | edited with an introduction and notes by Philip P. Wiener, Dover, | New York, NY, 1966. Originally published under the subtitle | in parentheses above, Doubleday & Company, 1958. But see CP 4.549-550 for a significant distinction between the categories (or modalities) and the orders of intention.
Discussion Note 17
HC = Howard Callaway
JA = Jon Awbrey
JA: In closing, observe that the teridentity relation has turned up again
in this context, as the second comma-ing of the universal term itself:
1,, = B:B:B +, C:C:C +, D:D:D +, E:E:E +, I:I:I +, J:J:J +, O:O:O.
HC: I see that you've come around to a mention of teridentity again, Jon.
Still, if I recall the prior discussions, then no one doubts that we
can have a system of notation in which teridentity appears (I don't
actually see it here).
Perhaps we could get at the root of the misunderstanding
if you tell me why you don't actually see the concept of
teridentity being exemplified here.
If it's only a matter of having lost the context of the
present discussion over the break, then you may find the
previous notes archived at the distal ends of the ur-links
that I append below (except for the first nine discussion
notes that got lost in a disk crash at the Arisbe Dev site).
HC: Also, I think we can have a system of notation in which
teridentity is needed. Those points seem reasonably clear.
The advantage of a concept is the integration of a species of manifold.
The necessity of a concept is the incapacity to integrate it otherwise.
Of course, no one should be too impressed with a concept that
is only the artifact of a particular system of representation.
So before we accord a concept the status of addressing reality,
and declare it a term of some tenured office in our intellects,
we would want to see some evidence that it helps us to manage
a reality that we cannot see a way to manage any other way.
Granted.
Now how in general do we go about an investiture of this sort?
That is the big question that would serve us well to consider
in the process of the more limited investigation of identity.
Indeed, I do not see how it is possible to answer the small
question if no understanding is reached on the big question.
HC: What remains relatively unclear is why we should need a system of notation
in which teridentity appears or is needed as against one in which it seems
not to be needed -- since assertion of identity can be made for any number
of terms in the standard predicate calculus.
This sort of statement totally non-plusses me.
It seems like a complete non-sequitur or even
a contradiction in terms to me.
The question is about the minimal adequate resource base for
defining, deriving, or generating all of the concepts that we
need for a given but very general type of application that we
conventionally but equivocally refer to as "logic". You seem
to be saying something like this: We don't need 3-identity
because we have 4-identity, 5-identity, 6-identity, ..., in
the "standard predicate calculus". The question is not what
concepts are generated in all the generations that follow the
establishment of the conceptual resource base (axiom system),
but what is the minimal set of concepts that we can use to
generate the needed collection of concepts. And there the
answer is, in a way that is subject to the usual sorts of
mathematical proof, that 3-identity is the minimum while
2-identity is not big enough to do the job we want to do.
Logic Of Relatives 01-41, LOR Discussion Notes 10-17.
Discussion Note 18
- Jon Awbrey
- but now I have to add to my do-list the problems of comparing the whole variorum of letters and drafts of letters to Lady Welby. I only have the CP 8 and Wiener versions here, so I will depend on you for ample excerpts from the Lieb volume.
- Bernard Morand
- I made such a kind of comparison some time ago. I selected the following 3 cases on the criterion of alternate "grounds". Hoping it could save some labor. The first rank expressions come from the MS 339 written in Oct. 1904 and I label them with an (a). I think that it is interesting to note that they were written four years before the letters to Welby and just one or two years after the Syllabus which is the usual reference for the classification in 3 trichotomies and 10 classes. The second (b) is our initial table (from a draft to Lady Welby, Dec. 1908, CP 8.344) and the third (c) comes from a letter sent in Dec. 1908 (CP 8.345–376). A tabular presentation would be better but I can't do it. Comparing (c) against (a) and (b) is informative, I think.
- Jon Awbrey
- Is this anywhere that it can be linked to from Arisbe? I've seen many pretty pictures of these things over the years, but may have to follow my own gnosis for a while.
- Pages I have bookmarked just recently, but not really had the chance to study:
- http://www.digitalpeirce.org/hoffmann/p-sighof.htm
- http://www.csd.uwo.ca/~merkle/thesis/Introduction.html
- http://members.door.net/arisbe/menu/library/aboutcsp/merkle/hci-abstract.htm
Discussion Note 19
BM = Bernard Morand
JA = Jon Awbrey
I now have three partially answered messages on the table,
so I will just grab this fragment off the top of the deck.
BM: Peirce gives the following definition (CP 8.343):
BM, quoting CSP:
| It is likewise requisite to distinguish
| the 'Immediate Interpretant', i.e. the
| Interpretant represented or signified in
| the Sign, from the 'Dynamic Interpretant',
| or effect actually produced on the mind
| by the Sign; and both of these from
| the 'Normal Interpretant', or effect
| that would be produced on the mind by
| the Sign after sufficient development
| of thought.
|
| C.S. Peirce, 'Collected Papers', CP 8.343.
JA: Well, you've really tossed me in the middle of the briar patch now!
I must continue with my reading from the 1870 LOR, ...
BM: Yes indeed! I am irritated by having not the necessary
turn of mind to fully grasp it. But it seems to be a
prerequisite in order to understand the very meaning
of the above table. It could be the same for:
BM, quoting CSP:
| I define a 'Sign' as anything which on the one hand
| is so determined by an Object and on the other hand
| so determines an idea in a person's mind, that this
| latter determination, which I term the 'Interpretant'
| of the sign, is thereby mediately determined by that
| Object.
BM: The so-called "latter determination" would make the 'Interpretant'
a tri-relative term into a teridentity involving Sign and Object.
Isn't it?
BM: I thought previously that the Peirce's phrasing was just applying the
principle of transitivity. From O determines S and S determines I,
it follows: O determines I. But this is not the same as teridentity.
Do you think so or otherwise?
My answers are "No" and "Otherwise".
Continuing to discourse about definite universes thereof,
the 3-identity term over the universe 1 = {A, B, C, D, ...} --
I only said it was definite, I didn't say it wasn't vague! --
designates, roughly speaking, the 3-adic relation that may
be hinted at by way of the following series:
1,, = A:A:A +, B:B:B +, C:C:C +, D:D:D +, ...
I did a study on Peirce's notion of "determination".
As I understand it so far, we need to keep in mind
that it is more fundamental than causation, can be
a form of "partial determination", and is roughly
formal, mathematical, or "information-theoretic",
not of necessity invoking any temporal order.
For example, when we say "The points A and B determine the line AB",
this invokes the concept of a 3-adic relation of determination that
does not identify A, B, AB, is not transitive, as transitivity has
to do with the composition of 2-adic relations and would amount to
the consideration of a degenerate 3-adic relation in this context.
Now, it is possible to have a sign relation q whose sum enlists
an elementary sign relation O:S:I where O = S = I. For example,
it makes perfect sense to me to say that the whole universe may
be a sign of itself to itself, so the conception is admissable.
But this amounts to a very special case, by no means general.
More generally, we are contemplating sums like the following:
q = O1:S1:I1 +, O2:S2:I2 +, O3:S3:I3 +, ...
Discussion Note 20
- Howard Callaway
- Though I certainly hesitate to think that we are separated from the world by a veil of signs, it seems clear, too, on Peircean grounds, that no sign can ever capture its object completely.
- Joe Ransdell
- Any case of self-representation is a case of sign-object identity, in some sense of “identity”. I have argued in various places that this is the key to the doctrine of immediate perception as it occurs in Peirce's theory.
- Jon Awbrey
- To put the phrase back on the lathe:
- We are not separated from the world by a veil of signs —
- we are the veil of signs.
Discussion Note 21
AS = Armando Sercovich
AS: We are not separated from the world by a veil of signs nor we are a veil of signs.
Simply we are signs.
AS, quoting CSP:
| The *man-sign* acquires information, and comes to mean more than he did before.
| But so do words. Does not electricity mean more now than it did in the days
| of Franklin? Man makes the word, and the word means nothing which the man
| has not made it mean, and that only to some man. But since man can think
| only by means of words or other external symbols, these might turn round
| and say: "You mean nothing which we have not taught you, and then only
| so far as you address some word as the interpretant of your thought".
| In fact, therefore, men and words reciprocally educate each other;
| each increase of a man's information involves, and is involved by,
| a corresponding increase of a word's information.
|
| Without fatiguing the reader by stretching this parallelism too far, it is
| sufficient to say that there is no element whatever of man's consciousness
| which has not something corresponding to it in the word; and the reason is
| obvious. It is that the word or sign which man uses *is* the man itself.
| For, as the fact that every thought is a sign, taken in conjunction with
| the fact that life is a train of thought, proves that man is a sign; so,
| that every thought is an *external* sign proves that man is an external
| sign. That is to say, the man and the external sign are identical, in
| the same sense in which the words 'homo' and 'man' are identical. Thus
| my language is the sum total of myself; for the man is the thought ...
|
|'Charles S. Peirce: Selected Writings (Values in a Universe of Chance)',
| edited with an introduction and notes by Philip P. Wiener, Dover,
| New York, NY, 1966. Originally published under the subtitle
| in parentheses above, Doubleday & Company, 1958.
I read you loud and clear.
Every manifold must have
its catalytic converter.
<Innumerate Continuation:>
TUC = The Usual CISPEC
TUC Alert:
| E.P.A. Says Catalytic Converter Is
| Growing Cause of Global Warming
| By Matthew L. Wald
| Copyright 1998 The New York Times
| May 29, 1998
| -----------------------------------------------------------------------
| WASHINGTON -- The catalytic converter, an invention that has sharply
| reduced smog from cars, has now become a significant and growing cause
| of global warming, according to the Environmental Protection Agency
Much as I would like to speculate ad libitum on these exciting new prospects for the
application of Peirce's chemico-algebraic theory of logic to the theorem-o-dynamics
of auto-semeiosis, I must get back to "business as usual" (BAU) ...
And now a word from our sponsor ...
http://www2.naias.com/
Reporting from Motown ---
Jon Awbrey
Discussion Note 22
HC = Howard Callaway
HC: You quote the following passage from a prior posting of mine:
HC: What remains relatively unclear is why we should need a system of notation
in which teridentity appears or is needed as against one in which it seems
not to be needed -- since assertion of identity can be made for any number
of terms in the standard predicate calculus.
HC: You comment as follows:
JA: This sort of statement totally non-plusses me.
It seems like a complete non-sequitur or even
a contradiction in terms to me.
JA: The question is about the minimal adequate resource base for
defining, deriving, or generating all of the concepts that we
need for a given but very general type of application that we
conventionally but equivocally refer to as "logic". You seem
to be saying something like this: We don't need 3-identity
because we have 4-identity, 5-identity, 6-identity, ..., in
the "standard predicate calculus". The question is not what
concepts are generated in all the generations that follow the
establishment of the conceptual resource base (axiom system),
but what is the minimal set of concepts that we can use to
generate the needed collection of concepts. And there the
answer is, in a way that is subject to the usual sorts of
mathematical proof, that 3-identity is the minimum while
2-identity is not big enough to do the job we want to do.
HC: I have fallen a bit behind on this thread while attending to some other
matters, but in this reply, you do seem to me to be coming around to an
understanding of the issues involved, as I see them. You put the matter
this way, "We don't need 3-identity because we have 4-identity, 5-identity,
6-identity, ..., in the 'standard predicate calculus'". Actually, as I think
you must know, there is no such thing as "4-identity", "5-identity", etc., in
the standard predicate calculus. It is more that such concepts are not needed,
just as teridentity is not needed, since the general apparatus of the predicate
calculus allows us to express identity among any number of terms without special
provision beyond "=".
No, that is not the case. Standard predicate calculus allows the expression
of predicates I_k, for k = 2, 3, 4, ..., such that I_k (x_1, ..., x_k) holds
if and only if all x_j, for j = 1 to k, are identical. So predicate calculus
contains a k-identity predicate for all such k. So whether "they're in there"
is not an issue. The question is whether these or any other predicates can be
constructed or defined in terms of 2-adic relations alone. And the answer is
no, they cannot. The vector of the misconception counterwise appears to be
as various a virus as the common cold, and every bit as resistant to cure.
I have taken the trouble to enumerate some of the more prevalent strains,
but most of them appear to go back to the 'Principia Mathematica', and
the variety of nominalism called "syntacticism" -- Ges-und-heit! --
that was spread by it, however unwittedly by some of its carriers.
Discussion Note 23
- Jon Awbrey
- In trying to answer the rest of your last note, it seems that we cannot go any further without achieving some concrete clarity as to what is denominated by “standard predicate calculus”, that is, “first order logic”, or whatever.
- There is a canonical presentation of the subject, as I remember it, anyway, in the following sample of materials from Chang and Keisler's Model Theory. (There's a newer edition of the book but this part of the subject hasn't really changed all that much in ages.)
- Model Theory 01-39
Discussion Note 24
HC = Howard Callaway
HC: I might object that "teridentity" seems to come
to a matter of "a=b & b=c", so that a specific
predicate of teridentity seems unnecessary.
I am presently concerned with expositing and interpreting
the logical system that Peirce laid out in the LOR of 1870.
It is my considered opinion after thirty years of study that
there are untapped resources remaining in this work that have
yet to make it through the filters of that ilk of syntacticism
that was all the rage in the late great 1900's. I find there
to be an appreciably different point of view on logic that is
embodied in Peirce's work, and until we have made the minimal
effort to read what he wrote it is just plain futile to keep
on pretending that we have already assimilated it, or that
we are qualified to evaluate its cogency.
The symbol "&" that you employ above denotes a mathematical object that
qualifies as a 3-adic relation. Independently of my own views, there
is an abundance of statements in evidence that mathematical thinkers
from Peirce to Goedel consider the appreciation of facts like this
to mark the boundary between realism and nominalism in regard to
mathematical objects.
Discussion Note 25
HC = Howard Callaway
JA = Jon Awbrey
HC: I might object that "teridentity" seems to come
to a matter of "a=b & b=c", so that a specific
predicate of teridentity seems unnecessary.
JA: I am presently concerned with expositing and interpreting
the logical system that Peirce laid out in the LOR of 1870.
It is my considered opinion after thirty years of study that
there are untapped resources remaining in this work that have
yet to make it through the filters of that ilk of syntacticism
that was all the rage in the late great 1900's. I find there
to be an appreciably different point of view on logic that is
embodied in Peirce's work, and until we have made the minimal
effort to read what he wrote it is just plain futile to keep
on pretending that we have already assimilated it, or that
we are qualified to evaluate its cogency.
JA: The symbol "&" that you employ above denotes a mathematical object that
qualifies as a 3-adic relation. Independently of my own views, there
is an abundance of statements in evidence that mathematical thinkers
from Peirce to Goedel consider the appreciation of facts like this
to mark the boundary between realism and nominalism in regard to
mathematical objects.
HC: I would agree, I think, that "&" may be thought of
as a function mapping pairs of statements onto the
conjunction of that pair.
Yes, indeed, in the immortal words of my very first college algebra book:
"A binary operation is a ternary relation". As it happens, the symbol "&"
is equivocal in its interpretation -- computerese today steals a Freudian
line and dubs it "polymorphous" -- it can be regarded in various contexts
as a 3-adic relation on syntactic elements called "sentences", on logical
elements called "propositions", or on truth values collated in the boolean
domain B = {false, true} = {0, 1}. But the mappings and relations between
all of these interpretive choices are moderately well understood. Still,
no matter how many ways you enumerate for looking at a B-bird, the "&" is
always 3-adic. And that is sufficient to meet your objection, so I think
I will just leave it there until next time.
On a related note, that I must postpone until later:
We seem to congrue that there is a skewness between
the way that most mathematicians use logic and some
philosophers talk about logic, but I may not be the
one to set it adjoint, much as I am inclined to try.
At the moment I have this long-post-poned exponency
to carry out. I will simply recommend for your due
consideration Peirce's 1870 Logic Of Relatives, and
leave it at that. There's a cornucopiousness to it
that's yet to be dreamt of in the philosophy of the
1900's. I am doing what I can to infotain you with
the Gardens of Mathematical Recreations that I find
within Peirce's work, and that's in direct response
to many, okay, a couple of requests. Perhaps I can
not hope to attain the degree of horticultural arts
that Gardners before me have exhibited in this work,
but then again, who could? Everybody's a critic --
but the better ones read first, and criticize later.
Discussion Note 26
- Howard Callaway
- But on the other hand, it is not customary to think of “&” as a relation among statements or sentences — as, for instance, logical implication is considered a logical relation between statements or sentences.
- Jon Awbrey
- Actually, it is the custom in many quarters to treat all of the boolean operations, logical connectives, propositional relations, or whatever you want to call them, as “equal citizens”, having each their “functional” (f : B^k -> B) and their “relational” (L c B^(k+1)) interpretations and applications. From this vantage, the interpretive distinction that is commonly regarded as that between “assertion” and mere “contemplation” is tantamount to a “pragmatic” difference between computing the values of a function on a given domain of arguments and computing the inverse of a function vis-a-vis a prospective true value. This is the logical analogue of the way that our mathematical models of reality have long been working, unsuspected and undisturbed by most philosophers of science, I might add. If only the logical side of the ledger were to be developed rather more fully than it is at present, we might wake one of these days to find our logical accounts of reality, finally, at long last, after an overweaningly longish adolescence, beginning to come of age.
Discussion Note 27
HC = Howard Callaway
HC: For, if I make an assertion A&B, then I am not asserting
that the statement A stands in a relation to a statement B.
Instead, I am asserting the conjunction A&B (which logically
implies both the conjuncts in view of the definition of "&").
Please try to remember where we came in. This whole play of
animadversions about 3-adicity and 3-identity is set against
the backdrop of a single point, over the issue as to whether
3-adic relations are wholly dispensable or somehow essential
to logic, mathematics, and indeed to argument, communication,
and reasoning in general. Some folks clamor "Off with their
unnecessary heads!" -- other people, who are forced by their
occupations to pay close attention to the ongoing complexity
of the processes at stake, know that, far from finding 3-ads
in this or that isolated corner of the realm, one can hardly
do anything at all in the ways of logging or mathing without
running smack dab into veritable hosts of them.
I have just shown that "a=b & b=c" involves a 3-adic relation.
Some people would consider this particular 3-adic relation to
be more complex than the 3-identity relation, but that may be
a question of taste. At any rate, the 3-adic aspect persists.
HC: If "&" counts as a triadic relation, simply because it serves
to conjoin two statements into a third, then it would seem that
any binary relation 'R' will count as triadic, simply because
it places two things into a relation, which is a "third" thing.
By the same kind of reasoning a triadic relation, as ordinarily
understood would be really 4-adic.
The rest of your comments are just confused,
and do not use the terms as they are defined.
Discussion Note 28
JA = Jon Awbrey
JR = Joseph Ransdell
JA: Notice that Peirce follows the mathematician's usual practice,
then and now, of making the status of being an "individual" or
a "universal" relative to a discourse in progress. I have come
to appreciate more and more of late how radically different this
"patchwork" or "piecewise" approach to things is from the way of
some philosophers who seem to be content with nothing less than
many worlds domination, which means that they are never content
and rarely get started toward the solution of any real problem.
Just my observation, I hope you understand.
JR: Yes, I take this as underscoring and explicating the import of
making logic prior to rather than dependent upon metaphysics.
I think that Peirce, and of course many math folks, would take math
as prior, on a par, or even identical with logic. Myself I've been
of many minds about this over the years. The succinctest picture
that I get from Peirce is always this one:
| [Riddle of the Sphynx]
|
| Normative science rests largely on phenomenology and on mathematics;
| Metaphysics on phenomenology and on normative science.
|
| C.S. Peirce, CP 1.186 (1903)
|
|
| o Metaphysics
| /|
| / |
| / |
| Normative Science o |
| / \ |
| / \ |
| / \|
| Mathematics o o Phenomenology
|
|
| ROTS. http://stderr.org/pipermail/inquiry/2004-March/001262.html
Logic being a normative science must depend on math and phenomenology.
Of course, it all depends on what a person means by "logic" ...
JA: I also observe that Peirce takes the individual objects of
a particular universe of discourse in a "generative" way,
not a "totalizing" way, and thus they afford us with the
basis for talking freely about collections, constructions,
properties, qualities, subsets, and "higher types", as
the phrase is mint.
JR: Would this be essentially the same as regarding quantification as
distributive rather than collective, i.e. we take the individuals
of a class one-by-one as selectable rather than as somehow given
all at once, collectively?
Gosh, that's a harder question. Your suggestion reminds me
of the way that some intuitionist and even some finitist
mathematicians talk when they reflect on math practice.
I have leanings that way, but when I have tried to
give up the classical logic axioms, I have found
them too built in to my way of thinking to quit.
Still, a healthy circumspection about about our
often-wrongly vaunted capacties to conceive of
totalities is a habitual part of current math.
Again, I think individuals are made not born,
that is, to some degree factitious and mere
compromises of this or that conveniency.
This is one of the reasons that I have
been trying to work out the details
of a functional approach to logic,
propostional, quantificational,
and relational.
Cf: INTRO 30. http://stderr.org/pipermail/inquiry/2004-November/001765.html
In: INTRO. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1720
Discussion Note 29
JA = Jon Awbrey
GR = Gary Richmond
Re: LOR.COM 11.24. http://stderr.org/pipermail/inquiry/2004-November/001836.html
In: LOR.COM. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1755
JA: The manner in which these arrows and qualified arrows help us
to construct a suspension bridge that unifies logic, semiotics,
statistics, stochastics, and information theory will be one of
the main themes that I aim to elaborate throughout the rest of
this inquiry.
GR: Pretty ambitious, Jon. I'm sure you're up to it.
GR: I'd like to anticipate 3 versions: The mathematical (cactus diagrams, etc.),
the poetic, and the commonsensical -- ordinary language for those who are
NEITHER logicians NOR poets.
GR: Are you up to THAT?
Riddle A Body: "Time Enough, And Space, Excalibrate Co-Arthurs Should Apply"
Discussion Note 30
JA = Jon Awbrey GR = Gary Richmond Re: LOR.DIS 29. http://stderr.org/pipermail/inquiry/2004-November/001838.html In: LOR.DIS. http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768 JA: Riddle A Body: "Time Enough, And Space, Excalibrate Co-Arthurs Should Apply" GR: Well said, and truly! Body A Riddle: TEASE CASA = Fun House.
Discussion Note 31
Many illusions of selective reading — like the myth that Peirce did not discover quantification over indices until 1885 — can be dispelled by looking into his 1870 “Logic of Relatives”. I started a web study of this in 2002, reworked again in 2003 and 2004, the current version of which can be found here:
I've only gotten as far as the bare infrastructure of Peirce's 1870 LOR, but an interesting feature of the study is that, if one draws the pictures that seem almost demanded by his way of linking up indices over expressions, then one can see a prototype of his much later logical graphs developing in the text.
Discussion Work Areas
Discussion Work Area 1
BM: Several discussions could take place there,
as to the reasons for the number of divisions,
the reasons of the titles themselves. Another
one is my translation from "normal interpretant"
into "final interpretant" (which one is called
elsewhere "Eventual Interpretant" or "Destinate
Interpretant" by CSP). I let all this aside
to focus on the following remark:
BM: 6 divisions correspond to individual correlates:
(S, O_i, O_d, I_i, I_d, I_n),
3 divisions correspond to dyads:
(S : O_d, S : I_d, S : I_n),
and the tenth to a triad:
(S : O_d : I_n).
This remark would itself deserve
a lot of explanations but one
more time I let this aside.
BM: Then we have the following very clear statement from Peirce:
| It follows from the Definition of a Sign
| that since the Dynamoid Object determines
| the Immediate Object,
| which determines the Sign,
| which determines the Destinate Interpretant
| which determines the Effective Interpretant
| which determines the Explicit Interpretant
|
| the six trichotomies, instead of determining 729 classes of signs,
| as they would if they were independent, only yield 28 classes; and
| if, as I strongly opine (not to say almost prove) there are four other
| trichotomies of signs of the same order of importance, instead of making
| 59049 classes, these will only come to 66.
|
| CSP, "Letter to Lady Welby", 14 Dec 1908, LW, p. 84.
BM: The separation made by CSP between 6 divisions and four others
seems to rely upon the suggested difference between individual
correlates and relations. We get the idea that the 10 divisions
are ordered on the whole and will end into 66 classes (by means of
three ordered modal values on each division: maybe, canbe, wouldbe).
Finally we have too the ordering for the divisions relative to the
correlates that I write in my notation:
Od -> Oi -> S -> If -> Id -> Ii.
BM: This order of "determinations" has bothered many people
but if we think of it as operative in semiosis, it seems
to be correct (at least to my eyes). Thus the question is:
where, how, and why the "four other trichotomies" fit in this
schema to obtain a linear ordering on the whole 10 divisions?
May be the question can be rephrased as: how intensional
relationships fit into an extensional one? Possibly the
question could be asked the other way. R. Marty responds
that in a certain sense the four trichotomies give nothing
more than the previous six ones but I strongly doubt of this.
BM: I put the problem in graphical form in an attached file
because my message editor will probably make some mistakes.
I make a distinction between arrow types drawing because I am
not sure that the sequence of correlates determinations is of
the same nature than correlates determination inside relations.
BM: It looks as if the problem amounts to some kind of projection
of relations on the horizontal axis made of correlates.
BM: If we consider some kind of equivalence (and this seems necessary to
obtain a linear ordering), by means of Agent -> Patient reductions on
relations, then erasing transitive determinations leads to:
Od -> Oi -> S -> S-Od -> If -> S-If -> S-Od-If -> Id -> S-Id -> Ii
BM: While it is interesting to compare the subsequence
S-Od -> If -> S-If -> S-Od-If with the pragmatic maxim,
I have no clear idea of the (in-) validity of such a result.
But I am convinced that the clarity has to come from the
Logic Of Relatives.
BM: I will be very grateful if you can make something with all that stuff.
Discussion Work Area 2
BM: I also found this passage which may be of some interest
(CP 4.540, Prolegomena to an Apology of Pragmatism):
| But though an Interpretant is not necessarily a Conclusion, yet a
| Conclusion is necessarily an Interpretant. So that if an Interpretant is
| not subject to the rules of Conclusions there is nothing monstrous in my
| thinking it is subject to some generalization of such rules. For any
| evolution of thought, whether it leads to a Conclusion or not, there is a
| certain normal course, which is to be determined by considerations not in
| the least psychological, and which I wish to expound in my next
| article;†1 and while I entirely agree, in opposition to distinguished
| logicians, that normality can be no criterion for what I call
| rationalistic reasoning, such as alone is admissible in science, yet it
| is precisely the criterion of instinctive or common-sense reasoning,
| which, within its own field, is much more trustworthy than rationalistic
| reasoning. In my opinion, it is self-control which makes any other than
| the normal course of thought possible, just as nothing else makes any
| other than the normal course of action possible; and just as it is
| precisely that that gives room for an ought-to-be of conduct, I mean
| Morality, so it equally gives room for an ought-to-be of thought, which
| is Right Reason; and where there is no self-control, nothing but the
| normal is possible. If your reflections have led you to a different
| conclusion from mine, I can still hope that when you come to read my next
| article, in which I shall endeavor to show what the forms of thought are,
| in general and in some detail, you may yet find that I have not missed
| the truth.
JA: Just as I have always feared, this classification mania
appears to be communicable! But now I must definitely
review the Welby correspondence, as all this stuff was
a blur to my sensibilities the last 10 times I read it.
BM: I think that I understand your reticence. I wonder if:
a. the fact that the letters to Lady Welby have been published as such,
has not lead to approach the matter in a certain way.
b. other sources, eventually unpublished, would give another lighting on
the subject, namely a logical one. I think of MS 339 for example that
seems to be part of the Logic Notebook. I have had access to some pages
of it, but not to the whole MS.
BM: A last remark. I don't think that classification is a mania for CSP but I
know that you know that! It is an instrument of thought and I think that
it is in this case much more a plan for experimenting than the exposition
of a conclusion. Experimenting what ? There is a strange statement in a
letter to W. James where CSP says that what is in question in his "second
way of dividing signs" is the logical theory of numbers. I give this from
memory. I have not the quote at hand now but I will search for it if needed.
Discussion Work Area 3
BM = Bernard Morand
JA = Jon Awbrey
JA: ... but now I have to add to my do-list the problems of comparing
the whole variorum of letters and drafts of letters to Lady Welby.
I only have the CP 8 and Wiener versions here, so I will depend
on you for ample excerpts from the Lieb volume.
BM: I made such a kind of comparison some time ago. I selected the following
3 cases on the criterium of alternate "grounds". Hoping it could save
some labor. The first rank expressions come from the MS 339 written in
Oct. 1904 and I label them with an (a). I think that it is interesting to
note that they were written four years before the letters to Welby and
just one or two years after the Syllabus which is the usual reference for
the classification in 3 trichotomies and 10 classes. The second (b) is
our initial table (from a draft to Lady Welby, Dec. 1908, CP 8.344) and
the third (c) comes from a letter sent in Dec. 1908 (CP 8.345-8.376). A
tabular presentation would be better but I can't do it. Comparing (c)
against (a) and (b) is informative, I think.
Division 1
(a) According to the matter of the Sign
(b) According to the Mode of Apprehension of the Sign itself
(c) Signs in respect to their Modes of possible Presentation
Division 2
(a) According to the Immediate Object
(b) According to the Mode of Presentation of the Immediate Object
(c) Objects, as they may be presented
Division 3
(a) According to the Matter of the Dynamic Object
(b) According to the Mode of Being of the Dynamical Object
(c) In respect to the Nature of the Dynamical Objects of Signs
Division 4
(a) According to the mode of representing object by the Dynamic Object
(b) According to the Relation of the Sign to its Dynamical Object
(c) The fourth Trichotomy
Division 5
(a) According to the Immédiate Interpretant
(b) According to the Mode of Presentation of the Immediate Interpretant
(c) As to the nature of the Immediate (or Felt ?) Interpretant
Division 6
(a) According to the Matter of Dynamic Interpretant
(b) According to the Mode of Being of the Dynamical Interpretant
(c) As to the Nature of the Dynamical Interpretant
Division 7
(a) According to the Mode of Affecting Dynamic Interpretant
(b) According to the relation of the Sign to the Dynamical Interpretant
(c) As to the Manner of Appeal to the Dynamic Interpretant
Division 8
(a) According to the Matter of Representative Interpretant
(b) According to the Nature of the Normal Interpretant
(c) According to the Purpose of the Eventual Interpretant
Division 9
(a) According to the Mode of being represented by Representative Interpretant
(b) According to the the relation of the Sign to the Normal Interpretant
(c) As to the Nature of the Influence of the Sign
Division 10
(a) According to the Mode of being represented to represent object by Sign, Truly
(b) According to the Triadic Relation of the Sign to its Dynamical Object and to
its Normal Interpretant
(c) As to the Nature of the Assurance of the Utterance
Discussion Work Area 4
JA: It may appear that one has side-stepped the issue of empiricism
that way, but then all that stuff about the synthetic a priori
raises its head, and we have Peirce's insight that mathematics
is observational and even experimental, and so I must trail off
into uncoordinated elliptical thoughts ...
HC: In contrast with this it strikes me that not all meanings of "analytic"
and "synthetic" have much, if anything, to do with the "analytic and the
synthetic", say, as in Quine's criticism of the "dualism" of empiricism.
Surely no one thinks that a plausible analysis must be analytic or that
synthetic materials tell us much about epistemology. So, it is not
clear that anything connected with analyticity or a priori knowledge
will plausibly or immediately arise from a discussion of analytical
geometry. Prevalent mathematical assumptions or postulates, yes --
but who says these are a prior? Can't non-Euclidean geometry also
be treated in the style of analytic geometry?
HC: I can imagine the a discussion might be forced in
that direction, but the connections don't strike me
as at all obvious or pressing. Perhaps Jon would just
like to bring up the notion of the synthetic apriori?
But why?
Discussion Work Area 5
HC = Howard Callaway
HC: But I see you as closer to my theme or challenge, when you say
"The question is about the minimal adequate resource base for
defining, deriving, or generating all of the concepts that we
need for a given but very general type of application that we
conventinally but equivocally refer to as 'logic'".
HC: I think it is accepted on all sides of the discussion that there
is some sort of "equivalence" between the standard predicate logic
and Peirce's graphs.
There you would be mistaken, except perhaps for the fact that
"some sort of equivalence" is vague to the depths of vacuity.
It most particularly does not mean "all sorts of equivalence"
or even "all important sorts of equivalence". It is usually
interpreted to mean an extremely abstract type of syntactic
equivalence, and that is undoubtedly one important type of
equivalence that it is worth examining whether two formal
systems have or not. But it precisely here that we find
another symptom of syntacticism, namely, the deprecation
of all other important qualities of formal systems, most
pointedly their "analystic, "semantic", and "pragmatic"
qualities, which make all the difference in how well the
system actually serves its users in a real world practice.
You can almost hear the whining and poohing coming from the
syntactic day camp, but those are the hard facts of the case.
HC: But we find this difference in relation to the vocabulary used to express
identity. From the point of view of starting with the predicate calculus,
we don't need "teridentity". So, this seems to suggest there is something
of interesting contrast in Peirce's logic, which brings in this concept.
The obvious question may be expressed by asking why we need teridentity
in Peirce's system and how Peirce's system may recommend itself in contrast
to the standard way with related concepts. This does seem to call for
a comparative evaluation of distinctive systems. That is not an easy task,
as I think we all understand. But I do think that if it is a goal to have
Peirce's system better appreciated, then that kind of question must be
addressed. If "=" is sufficient in the standard predicate calculus,
to say whatever we may need to say about the identity of terms, then
what is the advantage of an alternative system which insists on always
expressing identity of triples?
HC: The questions may look quite different, depending on where we start.
But in any case, I thought I saw some better appreciation of the
questions in your comments above.
Discussion Work Area 6
It's been that way for about as long as anybody can remember, and it will remain so, in spite of the spate of history rewriting and image re-engineering that has become the new rage in self-styled "analytic" circles.
Discussion Work Area 7
The brands of objection that you continue to make, with no evidence
of reflection on the many explanations that I and others have taken
the time to write out for you, lead me to believe that you are just
not interested in making that effort. That's okay, life is short,
the arts are long and many, there is always something else to do.
HC: For, if I make an assertion A&B, then I am not asserting
that the statement A stands in a relation to a statement B.
Instead, I am asserting the conjunction A&B (which logically
implies both the conjuncts in view of the definition of "&").
If "&" counts as a triadic relation, simply because it serves
to conjoin two statements into a third, then it would seem that
any binary relation 'R' will count as triadic, simply because
it places two things into a relation, which is a "third" thing.
By the same kind of reasoning a triadic relation, as ordinarily
understood would be really 4-adic.
HC: Now, I think this is the kind of argument you are making, ...
No, it's the kind of argument that you are making.
I am not making that kind of argument, and Peirce
did not make that kind of argument. Peirce used
his terms subject to definitions that would have
been understandable, and remain understandable,
to those of his readers who understand these
elementary definitions, either though their
prior acquaintance with standard concepts
or through their basic capacity to read
a well-formed, if novel definition.
Peirce made certain observations about the structure of logical concepts
and the structure of their referents. Those observations are accurate
and important. He expressed those observations in a form that is clear
to anybody who knows the meanings of the technical terms that he used,
and he is not responsible for the interpretations of those who don't.
HC: ... and it seems to both trivialize the claimed argument
for teridentity, by trivializing the conception of what
is to count as a triadic, as contrasted with a binary
relation, and it also seems to introduce a confusion
about what is is count as a binary, vs. a triadic
relation.
Yes, the argument that you are making trivializes
just about everything in sight, but that is the
common and well-known property of any argument
that fails to base itself on a grasp of the
first elements of the subject matter.
HC: If this is mathematical realism, then so much the worse for
mathematical realism. I am content to think that we do not
have a free hand in making up mathematical truth.
No, it's not mathematical realism. It is your reasoning,
and it exhibits all of the symptoms of syntacticism that
I have already diagnosed. It's a whole other culture
from what is pandemic in the practice of mathematics,
and it never fails to surprise me that people who
would never call themselves "relativists" in any
other matter of culture suddenly turn into just
that in matters of simple mathematical fact.
Work Area
Figure 51
Version 1
t_1 t_32 t_33 t_64 t_65 t_96 ... ...
o ... o o ... o o ... o o ... o U
\ | / \ | / \ | / \ | /
\ | / \ | / \ | / \ | / T
\|/ \|/ \|/ \|/
o o o o V
m_1 m_2 m_3 ...
|
Version 2
T_1 T_32 T_33 T_64 T_65 T_96 ... ...
o ... o o ... o o ... o o ... o t
\ | / \ | / \ | / \ | /
\ | / \ | / \ | / \ | / 't'
\|/ \|/ \|/ \|/
o o o o m
M_1 M_2 M_3 ...
|
Version 3
M_1 M_2 M_3 ...
o o o o m
/|\ /|\ /|\ /|\
/ | \ / | \ / | \ / | \ 't'
/ | \ / | \ / | \ / | \
o ... o o ... o o ... o o ... o t
T_1 T_32 T_33 T_64 T_65 T_96 ... ...
|
Mathematical Demonstration and the Doctrine of Individuals
CP 3.92
Selection from C.S. Peirce, “Logic Of Relatives” (1870), CP 3.45–149
92. Demonstration of the sort called mathematical is founded on suppositions of particular cases. The geometrician draws a figure; the algebraist assumes a letter to signify a single quantity fulfilling the required conditions. But while the mathematician supposes an individual case, his hypothesis is yet perfectly general, because he considers no characters of the individual case but those which must belong to every such case. The advantage of his procedure lies in the fact that the logical laws of individual terms are simpler than those which relate to general terms, because individuals are either identical or mutually exclusive, and cannot intersect or be subordinated to one another as classes can. Mathematical demonstration is not, therefore, more restricted to matters of intuition than any other kind of reasoning. Indeed, logical algebra conclusively proves that mathematics extends over the whole realm of formal logic; and any theory of cognition which cannot be adjusted to this fact must be abandoned. We may reap all the advantages which the mathematician is supposed to derive from intuition by simply making general suppositions of individual cases.
References
- Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic”, Memoirs of the American Academy of Arts and Sciences 9, 317–378, 26 January 1870. Reprinted, Collected Papers 3.45–149, Chronological Edition 2, 359–429. Online <a href="http://www.jstor.org/stable/25058006" target="_blank">(1)</a> <a href="https://archive.org/details/jstor-25058006" target="_blank">(2)</a> <a href="http://books.google.com/books?id=fFnWmf5oLaoC" target="_blank">(3)</a>.
- Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.
- Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.
Resources
- <a href="http://intersci.ss.uci.edu/wiki/index.php/Peirce%27s_1870_Logic_Of_Relatives" target="_blank" title="Peirce's 1870 Logic Of Relatives">Peirce's 1870 Logic Of Relatives</a>
CP 3.93
|
In reference to the doctrine of individuals, two distinctions should be borne in mind. The logical atom, or term not capable of logical division, must be one of which every predicate may be universally affirmed or denied. For, let \(\mathrm{A}\!\) be such a term. Then, if it is neither true that all \(\mathrm{A}\!\) is \(\mathrm{X}\!\) nor that no \(\mathrm{A}\!\) is \(\mathrm{X},\!\) it must be true that some \(\mathrm{A}\!\) is \(\mathrm{X}\!\) and some \(\mathrm{A}\!\) is not \(\mathrm{X};\!\) and therefore \(\mathrm{A}\!\) may be divided into \(\mathrm{A}\!\) that is \(\mathrm{X}\!\) and \(\mathrm{A}\!\) that is not \(\mathrm{X},\!\) which is contrary to its nature as a logical atom. Such a term can be realized neither in thought nor in sense. Not in sense, because our organs of sense are special — the eye, for example, not immediately informing us of taste, so that an image on the retina is indeterminate in respect to sweetness and non-sweetness. When I see a thing, I do not see that it is not sweet, nor do I see that it is sweet; and therefore what I see is capable of logical division into the sweet and the not sweet. It is customary to assume that visual images are absolutely determinate in respect to color, but even this may be doubted. I know no facts which prove that there is never the least vagueness in the immediate sensation. In thought, an absolutely determinate term cannot be realized, because, not being given by sense, such a concept would have to be formed by synthesis, and there would be no end to the synthesis because there is no limit to the number of possible predicates. A logical atom, then, like a point in space, would involve for its precise determination an endless process. We can only say, in a general way, that a term, however determinate, may be made more determinate still, but not that it can be made absolutely determinate. Such a term as “the second Philip of Macedon” is still capable of logical division — into Philip drunk and Philip sober, for example; but we call it individual because that which is denoted by it is in only one place at one time. It is a term not absolutely indivisible, but indivisible as long as we neglect differences of time and the differences which accompany them. Such differences we habitually disregard in the logical division of substances. In the division of relations, etc., we do not, of course, disregard these differences, but we disregard some others. There is nothing to prevent almost any sort of difference from being conventionally neglected in some discourse, and if \(I\!\) be a term which in consequence of such neglect becomes indivisible in that discourse, we have in that discourse, \([I] = 1.\!\) This distinction between the absolutely indivisible and that which is one in number from a particular point of view is shadowed forth in the two words individual (τὸ ἄτομον) and singular (τὸ καθ᾿ ἕκαστον); but as those who have used the word individual have not been aware that absolute individuality is merely ideal, it has come to be used in a more general sense. (CP 3.93, CE 2, 389–390). Charles Sanders Peirce, “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic”, Memoirs of the American Academy, Volume 9, pp. 317–378, 26 January 1870, Collected Papers (CP 3.45–149), Chronological Edition (CE 2, 359–429). |
Note. On the square bracket notation used above: Peirce explains this notation at CP 3.65.
I propose to denote the number of a logical term by enclosing the term in square brackets, thus, \([t].\!\) |
The number of an absolute term, as in the case of \(I,\!\) is defined as the number of individuals it denotes.
Document History
2002 • Peirce List
2002–2003 • Ontology List
- http://web.archive.org/web/20070302144532/http://suo.ieee.org/ontology/thrd20.html#04416
- http://web.archive.org/web/20070304201457/http://suo.ieee.org/ontology/thrd21.html#04425
- http://web.archive.org/web/20070302144532/http://suo.ieee.org/ontology/thrd20.html#04455
- http://web.archive.org/web/20070225053324/http://suo.ieee.org/ontology/thrd22.html#04515
- http://web.archive.org/web/20070302152249/http://suo.ieee.org/ontology/msg04416.html
- http://web.archive.org/web/20070304003617/http://suo.ieee.org/ontology/msg04417.html
- http://web.archive.org/web/20070303180330/http://suo.ieee.org/ontology/msg04418.html
- http://web.archive.org/web/20070304003631/http://suo.ieee.org/ontology/msg04419.html
- http://web.archive.org/web/20070304003523/http://suo.ieee.org/ontology/msg04421.html
- http://web.archive.org/web/20070304003534/http://suo.ieee.org/ontology/msg04422.html
- http://web.archive.org/web/20070304003546/http://suo.ieee.org/ontology/msg04423.html
- http://web.archive.org/web/20070303180343/http://suo.ieee.org/ontology/msg04424.html
- http://web.archive.org/web/20070304003512/http://suo.ieee.org/ontology/msg04425.html
- http://web.archive.org/web/20070304003646/http://suo.ieee.org/ontology/msg04426.html
- http://web.archive.org/web/20070304003657/http://suo.ieee.org/ontology/msg04427.html
- http://web.archive.org/web/20070303180353/http://suo.ieee.org/ontology/msg04431.html
- http://web.archive.org/web/20070304003707/http://suo.ieee.org/ontology/msg04432.html
- http://web.archive.org/web/20070304003718/http://suo.ieee.org/ontology/msg04435.html
- http://web.archive.org/web/20070304003452/http://suo.ieee.org/ontology/msg04436.html
- http://web.archive.org/web/20070303180403/http://suo.ieee.org/ontology/msg04437.html
- http://web.archive.org/web/20070304003728/http://suo.ieee.org/ontology/msg04438.html
- http://web.archive.org/web/20070303180414/http://suo.ieee.org/ontology/msg04439.html
- http://web.archive.org/web/20070304003423/http://suo.ieee.org/ontology/msg04440.html
- http://web.archive.org/web/20070304003502/http://suo.ieee.org/ontology/msg04441.html
- http://web.archive.org/web/20070304003738/http://suo.ieee.org/ontology/msg04442.html
- http://web.archive.org/web/20070304003748/http://suo.ieee.org/ontology/msg04443.html
- http://web.archive.org/web/20070304003432/http://suo.ieee.org/ontology/msg04444.html
- http://web.archive.org/web/20070303180423/http://suo.ieee.org/ontology/msg04445.html
- http://web.archive.org/web/20070304003758/http://suo.ieee.org/ontology/msg04446.html
- http://web.archive.org/web/20070304003809/http://suo.ieee.org/ontology/msg04447.html
- http://web.archive.org/web/20070304003818/http://suo.ieee.org/ontology/msg04448.html
- http://web.archive.org/web/20070304003829/http://suo.ieee.org/ontology/msg04449.html
- http://web.archive.org/web/20070304003842/http://suo.ieee.org/ontology/msg04450.html
- http://web.archive.org/web/20070304003853/http://suo.ieee.org/ontology/msg04451.html
- http://web.archive.org/web/20070304003903/http://suo.ieee.org/ontology/msg04452.html
- http://web.archive.org/web/20070304003913/http://suo.ieee.org/ontology/msg04453.html
- http://web.archive.org/web/20070304003923/http://suo.ieee.org/ontology/msg04454.html
- http://web.archive.org/web/20070303180434/http://suo.ieee.org/ontology/msg04456.html
- http://web.archive.org/web/20070304003933/http://suo.ieee.org/ontology/msg04457.html
- http://web.archive.org/web/20070304003943/http://suo.ieee.org/ontology/msg04458.html
- http://web.archive.org/web/20070304003954/http://suo.ieee.org/ontology/msg04459.html
- http://web.archive.org/web/20070304004004/http://suo.ieee.org/ontology/msg04462.html
- http://web.archive.org/web/20070304004014/http://suo.ieee.org/ontology/msg04464.html
- http://web.archive.org/web/20070304004024/http://suo.ieee.org/ontology/msg04473.html
- http://web.archive.org/web/20070304004034/http://suo.ieee.org/ontology/msg04478.html
- http://web.archive.org/web/20070303180444/http://suo.ieee.org/ontology/msg04484.html
- http://web.archive.org/web/20070304004044/http://suo.ieee.org/ontology/msg04487.html
- http://web.archive.org/web/20070303180454/http://suo.ieee.org/ontology/msg04488.html
- http://web.archive.org/web/20070304004054/http://suo.ieee.org/ontology/msg04492.html
- http://web.archive.org/web/20070303180504/http://suo.ieee.org/ontology/msg04497.html
- http://web.archive.org/web/20070303180514/http://suo.ieee.org/ontology/msg04498.html
- http://web.archive.org/web/20070304004104/http://suo.ieee.org/ontology/msg04499.html
- http://web.archive.org/web/20070304004114/http://suo.ieee.org/ontology/msg04500.html
- http://web.archive.org/web/20070304004126/http://suo.ieee.org/ontology/msg04501.html
- http://web.archive.org/web/20070304004137/http://suo.ieee.org/ontology/msg04502.html
- http://web.archive.org/web/20070304004147/http://suo.ieee.org/ontology/msg04503.html
- http://web.archive.org/web/20070304004158/http://suo.ieee.org/ontology/msg04504.html
- http://web.archive.org/web/20070303180524/http://suo.ieee.org/ontology/msg04506.html
- http://web.archive.org/web/20070302152300/http://suo.ieee.org/ontology/msg04508.html
- http://web.archive.org/web/20070302152309/http://suo.ieee.org/ontology/msg04509.html
- http://web.archive.org/web/20070302152319/http://suo.ieee.org/ontology/msg04510.html
- http://web.archive.org/web/20070302152329/http://suo.ieee.org/ontology/msg04511.html
- http://web.archive.org/web/20070228081319/http://suo.ieee.org/ontology/msg04512.html
- http://web.archive.org/web/20070228081328/http://suo.ieee.org/ontology/msg04513.html
- http://web.archive.org/web/20070228081356/http://suo.ieee.org/ontology/msg04516.html
- http://web.archive.org/web/20070228081406/http://suo.ieee.org/ontology/msg04517.html
- http://web.archive.org/web/20070228081419/http://suo.ieee.org/ontology/msg04518.html
- http://web.archive.org/web/20070228081429/http://suo.ieee.org/ontology/msg04521.html
- http://web.archive.org/web/20070228081440/http://suo.ieee.org/ontology/msg04539.html
- http://web.archive.org/web/20070228081449/http://suo.ieee.org/ontology/msg04541.html
- http://web.archive.org/web/20070228081501/http://suo.ieee.org/ontology/msg04542.html
- http://web.archive.org/web/20070228081512/http://suo.ieee.org/ontology/msg04543.html
- http://web.archive.org/web/20070228081347/http://suo.ieee.org/ontology/msg04515.html
2003 • Ontology List • Discussion
- http://web.archive.org/web/20070305104636/http://suo.ieee.org/ontology/msg04460.html
- http://web.archive.org/web/20070305123739/http://suo.ieee.org/ontology/msg04461.html
- http://web.archive.org/web/20070305103313/http://suo.ieee.org/ontology/msg04471.html
- http://web.archive.org/web/20070305104646/http://suo.ieee.org/ontology/msg04472.html
- http://web.archive.org/web/20070305201820/http://suo.ieee.org/ontology/msg04475.html
- http://web.archive.org/web/20070305104656/http://suo.ieee.org/ontology/msg04476.html
- http://web.archive.org/web/20070305104706/http://suo.ieee.org/ontology/msg04477.html
- http://web.archive.org/web/20070305104716/http://suo.ieee.org/ontology/msg04479.html
- http://web.archive.org/web/20070305104727/http://suo.ieee.org/ontology/msg04480.html
- http://web.archive.org/web/20070305104746/http://suo.ieee.org/ontology/msg04481.html
- http://web.archive.org/web/20070307071521/http://suo.ieee.org/ontology/msg04482.html
- http://web.archive.org/web/20040730203244/http://suo.ieee.org/ontology/msg04483.html
- http://web.archive.org/web/20070305104801/http://suo.ieee.org/ontology/msg04485.html
- http://web.archive.org/web/20040729135710/http://suo.ieee.org/ontology/msg04486.html
- http://web.archive.org/web/20070305104812/http://suo.ieee.org/ontology/msg04493.html
- http://web.archive.org/web/20070305104822/http://suo.ieee.org/ontology/msg04494.html
- http://web.archive.org/web/20070305104832/http://suo.ieee.org/ontology/msg04495.html
- http://web.archive.org/web/20070305104842/http://suo.ieee.org/ontology/msg04496.html
2003 • Arisbe List
- http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1453
- http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1485
- http://web.archive.org/web/20140617201402/http://stderr.org/pipermail/arisbe/2003-January/thread.html#1505
- http://web.archive.org/web/20140619114718/http://stderr.org/pipermail/arisbe/2003-February/thread.html#1520
- http://web.archive.org/web/20140617201423/http://stderr.org/pipermail/arisbe/2003-January/001453.html
- http://web.archive.org/web/20050506011725/http://stderr.org/pipermail/arisbe/2003-January/001454.html
- http://web.archive.org/web/20050506011629/http://stderr.org/pipermail/arisbe/2003-January/001457.html
- http://web.archive.org/web/20050506011625/http://stderr.org/pipermail/arisbe/2003-January/001461.html
- http://web.archive.org/web/20050506011649/http://stderr.org/pipermail/arisbe/2003-January/001467.html
- http://web.archive.org/web/20050506011653/http://stderr.org/pipermail/arisbe/2003-January/001470.html
- http://web.archive.org/web/20051202053753/http://stderr.org/pipermail/arisbe/2003-January/001471.html
- http://web.archive.org/web/20050824084910/http://stderr.org/pipermail/arisbe/2003-January/001475.html
- http://web.archive.org/web/20051202075602/http://stderr.org/pipermail/arisbe/2003-January/001480.html
- http://web.archive.org/web/20050826203125/http://stderr.org/pipermail/arisbe/2003-January/001481.html
- http://web.archive.org/web/20051202045453/http://stderr.org/pipermail/arisbe/2003-January/001482.html
- http://web.archive.org/web/20051202035157/http://stderr.org/pipermail/arisbe/2003-January/001483.html
- http://web.archive.org/web/20051202053307/http://stderr.org/pipermail/arisbe/2003-January/001484.html
- http://web.archive.org/web/20051202042621/http://stderr.org/pipermail/arisbe/2003-January/001485.html
- http://web.archive.org/web/20051202070136/http://stderr.org/pipermail/arisbe/2003-January/001486.html
- http://web.archive.org/web/20051202011212/http://stderr.org/pipermail/arisbe/2003-January/001488.html
- http://web.archive.org/web/20050506090030/http://stderr.org/pipermail/arisbe/2003-January/001489.html
- http://web.archive.org/web/20050506090129/http://stderr.org/pipermail/arisbe/2003-January/001503.html
- http://web.archive.org/web/20050506090050/http://stderr.org/pipermail/arisbe/2003-January/001505.html
- http://web.archive.org/web/20050506090219/http://stderr.org/pipermail/arisbe/2003-January/001507.html
- http://web.archive.org/web/20050506090106/http://stderr.org/pipermail/arisbe/2003-January/001513.html
- http://web.archive.org/web/20050506090223/http://stderr.org/pipermail/arisbe/2003-January/001514.html
- http://web.archive.org/web/20050506090154/http://stderr.org/pipermail/arisbe/2003-January/001515.html
- http://web.archive.org/web/20070315211932/http://stderr.org/pipermail/arisbe/2003-February/001520.html
- http://web.archive.org/web/20070315211952/http://stderr.org/pipermail/arisbe/2003-February/001525.html
- http://web.archive.org/web/20070315212032/http://stderr.org/pipermail/arisbe/2003-February/001529.html
- http://web.archive.org/web/20070315212112/http://stderr.org/pipermail/arisbe/2003-February/001534.html
- http://web.archive.org/web/20070315163838/http://stderr.org/pipermail/arisbe/2003-February/001567.html
- http://web.archive.org/web/20070315212724/http://stderr.org/pipermail/arisbe/2003-February/001578.html
- http://web.archive.org/web/20070315212733/http://stderr.org/pipermail/arisbe/2003-February/001579.html
- http://web.archive.org/web/20070315212814/http://stderr.org/pipermail/arisbe/2003-February/001587.html
2003 • Arisbe List • Discussion
- http://web.archive.org/web/20051202040453/http://stderr.org/pipermail/arisbe/2003-January/001455.html
- http://web.archive.org/web/20050826052233/http://stderr.org/pipermail/arisbe/2003-January/001456.html
- http://web.archive.org/web/20050506011705/http://stderr.org/pipermail/arisbe/2003-January/001458.html
- http://web.archive.org/web/20050506011657/http://stderr.org/pipermail/arisbe/2003-January/001459.html
- http://web.archive.org/web/20050506011857/http://stderr.org/pipermail/arisbe/2003-January/001460.html
- http://web.archive.org/web/20050506011701/http://stderr.org/pipermail/arisbe/2003-January/001462.html
- http://web.archive.org/web/20050826112404/http://stderr.org/pipermail/arisbe/2003-January/001463.html
- http://web.archive.org/web/20051202065741/http://stderr.org/pipermail/arisbe/2003-January/001464.html
- http://web.archive.org/web/20050827050454/http://stderr.org/pipermail/arisbe/2003-January/001465.html
- http://web.archive.org/web/20051202100823/http://stderr.org/pipermail/arisbe/2003-January/001466.html
- http://web.archive.org/web/20050506011801/http://stderr.org/pipermail/arisbe/2003-January/001468.html
- http://web.archive.org/web/20050824223011/http://stderr.org/pipermail/arisbe/2003-January/001469.html
- http://web.archive.org/web/20050506011633/http://stderr.org/pipermail/arisbe/2003-January/001476.html
- http://web.archive.org/web/20050506011849/http://stderr.org/pipermail/arisbe/2003-January/001477.html
- http://web.archive.org/web/20050826141451/http://stderr.org/pipermail/arisbe/2003-January/001478.html
- http://web.archive.org/web/20050506011845/http://stderr.org/pipermail/arisbe/2003-January/001479.html
2003 • Inquiry List
- http://web.archive.org/web/20150224210000/http://stderr.org/pipermail/inquiry/2003-March/thread.html#186
- http://web.archive.org/web/20150302021003/http://stderr.org/pipermail/inquiry/2003-April/thread.html#245
- http://web.archive.org/web/20081120062116/http://stderr.org/pipermail/inquiry/2003-March/000186.html
- http://web.archive.org/web/20061013222246/http://stderr.org/pipermail/inquiry/2003-March/000187.html
- http://web.archive.org/web/20061013221536/http://stderr.org/pipermail/inquiry/2003-March/000188.html
- http://web.archive.org/web/20061013222728/http://stderr.org/pipermail/inquiry/2003-March/000189.html
- http://web.archive.org/web/20061013222333/http://stderr.org/pipermail/inquiry/2003-March/000190.html
- http://web.archive.org/web/20061013221823/http://stderr.org/pipermail/inquiry/2003-March/000191.html
- http://web.archive.org/web/20070305235828/http://stderr.org/pipermail/inquiry/2003-March/000194.html
- http://web.archive.org/web/20070302055237/http://stderr.org/pipermail/inquiry/2003-March/000195.html
- http://web.archive.org/web/20070303020850/http://stderr.org/pipermail/inquiry/2003-April/000245.html
- http://web.archive.org/web/20070306225534/http://stderr.org/pipermail/inquiry/2003-April/000246.html
- http://web.archive.org/web/20070315063236/http://stderr.org/pipermail/inquiry/2003-April/000247.html
- http://web.archive.org/web/20070310205044/http://stderr.org/pipermail/inquiry/2003-April/000248.html
- http://web.archive.org/web/20070310205014/http://stderr.org/pipermail/inquiry/2003-April/000249.html
- http://web.archive.org/web/20061013223819/http://stderr.org/pipermail/inquiry/2003-April/000250.html
- http://web.archive.org/web/20070310204954/http://stderr.org/pipermail/inquiry/2003-April/000251.html
- http://web.archive.org/web/20070309174344/http://stderr.org/pipermail/inquiry/2003-April/000252.html
- http://web.archive.org/web/20070310205054/http://stderr.org/pipermail/inquiry/2003-April/000253.html
- http://web.archive.org/web/20070310205024/http://stderr.org/pipermail/inquiry/2003-April/000254.html
- http://web.archive.org/web/20070310205034/http://stderr.org/pipermail/inquiry/2003-April/000255.html
- http://web.archive.org/web/20070310205105/http://stderr.org/pipermail/inquiry/2003-April/000256.html
- http://web.archive.org/web/20070310205116/http://stderr.org/pipermail/inquiry/2003-April/000257.html
- http://web.archive.org/web/20070309174424/http://stderr.org/pipermail/inquiry/2003-April/000258.html
- http://web.archive.org/web/20070311141543/http://stderr.org/pipermail/inquiry/2003-April/000259.html
- http://web.archive.org/web/20070309202630/http://stderr.org/pipermail/inquiry/2003-April/000260.html
- http://web.archive.org/web/20070309202751/http://stderr.org/pipermail/inquiry/2003-April/000261.html
- http://web.archive.org/web/20070309174451/http://stderr.org/pipermail/inquiry/2003-April/000262.html
- http://web.archive.org/web/20070309202431/http://stderr.org/pipermail/inquiry/2003-April/000263.html
- http://web.archive.org/web/20070310204947/http://stderr.org/pipermail/inquiry/2003-April/000264.html
- http://web.archive.org/web/20070309202640/http://stderr.org/pipermail/inquiry/2003-April/000265.html
- http://web.archive.org/web/20070309202441/http://stderr.org/pipermail/inquiry/2003-April/000267.html
- http://web.archive.org/web/20070310205004/http://stderr.org/pipermail/inquiry/2003-April/000268.html
- http://web.archive.org/web/20061013223536/http://stderr.org/pipermail/inquiry/2003-April/000269.html
- http://web.archive.org/web/20070309202731/http://stderr.org/pipermail/inquiry/2003-April/000270.html
- http://web.archive.org/web/20061013223302/http://stderr.org/pipermail/inquiry/2003-April/000271.html
- http://web.archive.org/web/20070310205134/http://stderr.org/pipermail/inquiry/2003-April/000273.html
- http://web.archive.org/web/20070310205146/http://stderr.org/pipermail/inquiry/2003-April/000274.html
- http://web.archive.org/web/20070310075558/http://stderr.org/pipermail/inquiry/2003-April/000275.html
- http://web.archive.org/web/20070309174501/http://stderr.org/pipermail/inquiry/2003-April/000276.html
- http://web.archive.org/web/20070311141604/http://stderr.org/pipermail/inquiry/2003-April/000277.html
- http://web.archive.org/web/20070309202651/http://stderr.org/pipermail/inquiry/2003-April/000278.html
- http://web.archive.org/web/20070311141625/http://stderr.org/pipermail/inquiry/2003-April/000279.html
- http://web.archive.org/web/20070310205157/http://stderr.org/pipermail/inquiry/2003-April/000280.html
- http://web.archive.org/web/20070310205207/http://stderr.org/pipermail/inquiry/2003-April/000281.html
- http://web.archive.org/web/20070309174530/http://stderr.org/pipermail/inquiry/2003-April/000282.html
- http://web.archive.org/web/20070310205217/http://stderr.org/pipermail/inquiry/2003-April/000283.html
- http://web.archive.org/web/20070310205228/http://stderr.org/pipermail/inquiry/2003-April/000284.html
- http://web.archive.org/web/20070309202710/http://stderr.org/pipermail/inquiry/2003-April/000285.html
- http://web.archive.org/web/20070310205237/http://stderr.org/pipermail/inquiry/2003-April/000286.html
- http://web.archive.org/web/20070310205247/http://stderr.org/pipermail/inquiry/2003-April/000287.html
- http://web.archive.org/web/20070309202720/http://stderr.org/pipermail/inquiry/2003-April/000288.html
- http://web.archive.org/web/20061013223711/http://stderr.org/pipermail/inquiry/2003-April/000289.html
- http://web.archive.org/web/20070310205257/http://stderr.org/pipermail/inquiry/2003-April/000290.html
- http://web.archive.org/web/20061013223830/http://stderr.org/pipermail/inquiry/2003-April/000291.html
- http://web.archive.org/web/20070310205307/http://stderr.org/pipermail/inquiry/2003-April/000294.html
- http://web.archive.org/web/20061013224103/http://stderr.org/pipermail/inquiry/2003-April/000295.html
- http://web.archive.org/web/20070310205317/http://stderr.org/pipermail/inquiry/2003-April/000296.html
- http://web.archive.org/web/20070310095852/http://stderr.org/pipermail/inquiry/2003-April/000297.html
- http://web.archive.org/web/20061013223138/http://stderr.org/pipermail/inquiry/2003-April/000298.html
- http://web.archive.org/web/20070310205328/http://stderr.org/pipermail/inquiry/2003-April/000299.html
- http://web.archive.org/web/20061013223241/http://stderr.org/pipermail/inquiry/2003-April/000300.html
- http://web.archive.org/web/20081120085752/http://stderr.org/pipermail/inquiry/2003-April/000301.html
- http://web.archive.org/web/20070310205349/http://stderr.org/pipermail/inquiry/2003-April/000302.html
- http://web.archive.org/web/20070311141532/http://stderr.org/pipermail/inquiry/2003-April/000303.html
- http://web.archive.org/web/20070309203110/http://stderr.org/pipermail/inquiry/2003-April/000305.html
- http://web.archive.org/web/20070310205359/http://stderr.org/pipermail/inquiry/2003-April/000306.html
- http://web.archive.org/web/20070310205409/http://stderr.org/pipermail/inquiry/2003-April/000307.html
- http://web.archive.org/web/20070310204919/http://stderr.org/pipermail/inquiry/2003-April/000308.html
- http://web.archive.org/web/20070310205420/http://stderr.org/pipermail/inquiry/2003-April/000309.html
2004 • Inquiry List • Selections
- http://web.archive.org/web/20060217232934/http://stderr.org/pipermail/inquiry/2004-November/001750.html
- http://web.archive.org/web/20081120211119/http://stderr.org/pipermail/inquiry/2004-November/001751.html
- http://web.archive.org/web/20081120205154/http://stderr.org/pipermail/inquiry/2004-November/001752.html
- http://web.archive.org/web/20060217232947/http://stderr.org/pipermail/inquiry/2004-November/001753.html
- http://web.archive.org/web/20081120202444/http://stderr.org/pipermail/inquiry/2004-November/001754.html
- http://web.archive.org/web/20081120202147/http://stderr.org/pipermail/inquiry/2004-November/001760.html
- http://web.archive.org/web/20081120191806/http://stderr.org/pipermail/inquiry/2004-November/001769.html
- http://web.archive.org/web/20081120212429/http://stderr.org/pipermail/inquiry/2004-November/001774.html
- http://web.archive.org/web/20120222231523/http://stderr.org/pipermail/inquiry/2004-November/001783.html
- http://web.archive.org/web/20120222231525/http://stderr.org/pipermail/inquiry/2004-November/001794.html
- http://web.archive.org/web/20060217233454/http://stderr.org/pipermail/inquiry/2004-November/001812.html
- http://web.archive.org/web/20060217233731/http://stderr.org/pipermail/inquiry/2004-November/001842.html
2004 • Inquiry List • Comments
2004–2009 • Inquiry List • Discussion
- http://web.archive.org/web/20150302042625/http://stderr.org/pipermail/inquiry/2004-November/thread.html#1768
- http://web.archive.org/web/20061013215458/http://stderr.org/pipermail/inquiry/2005-January/thread.html#2301
- http://web.archive.org/web/20120428203121/http://stderr.org/pipermail/inquiry/2009-April/thread.html#3548
- http://web.archive.org/web/20120222232055/http://stderr.org/pipermail/inquiry/2004-November/001768.html
- http://web.archive.org/web/20120222232057/http://stderr.org/pipermail/inquiry/2004-November/001838.html
- http://web.archive.org/web/20120222232101/http://stderr.org/pipermail/inquiry/2004-November/001840.html
- http://web.archive.org/web/20061014002508/http://stderr.org/pipermail/inquiry/2005-January/002301.html
- http://web.archive.org/web/20120206222034/http://stderr.org/pipermail/inquiry/2009-April/003548.html