Directory:Jon Awbrey/Papers/Differential Logic

Differential logic is the component of logic whose object is the description of variation — for example, the aspects of change, difference, distribution, and diversity — in universes of discourse that are subject to logical description. In formal logic, differential logic treats the principles that govern the use of a differential logical calculus, that is, a formal system with the expressive capacity to describe change and diversity in logical universes of discourse.

A simple example of a differential logical calculus is furnished by a differential propositional calculus. A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe. This augments ordinary propositional calculus in the same way that the differential calculus of Leibniz and Newton augments the analytic geometry of Descartes.

Note 1

One of the first things that you can do, once you have a really decent calculus for boolean functions or propositional logic, whatever you want to call it, is to compute the differentials of these functions or propositions.

Now there are many ways to dance around this idea, and I feel like I have tried them all, before one gets down to acting on it, and there many issues of interpretation and justification that we will have to clear up after the fact, that is, before we can be sure that it all really makes any sense, but I think this time I'll just jump in, and show you the form in which this idea first came to me.

Start with a proposition of the form \(x ~\operatorname{and}~ y,\) which is graphed as two labels attached to a root node:

o---------------------------------------o | | | x y | | @ | | | o---------------------------------------o | x and y | o---------------------------------------o

Written as a string, this is just the concatenation "\(x~y\)".

The proposition \(xy\!\) may be taken as a boolean function \(f(x, y)\!\) having the abstract type \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B},\) where \(\mathbb{B} = \{ 0, 1 \}\) is read in such a way that \(0\!\) means \(\operatorname{false}\) and \(1\!\) means \(\operatorname{true}.\)

In this style of graphical representation, the value \(\operatorname{true}\) looks like a blank label and the value \(\operatorname{false}\) looks like an edge.

o---------------------------------------o | | | | | @ | | | o---------------------------------------o | true | o---------------------------------------o

o---------------------------------------o | | | o | | | | | @ | | | o---------------------------------------o | false | o---------------------------------------o

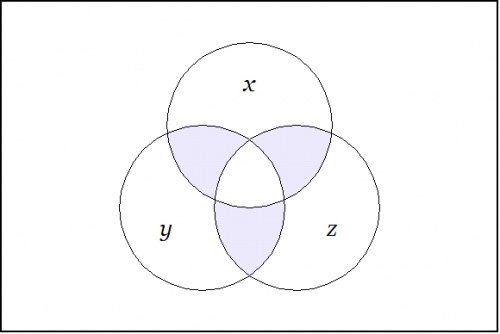
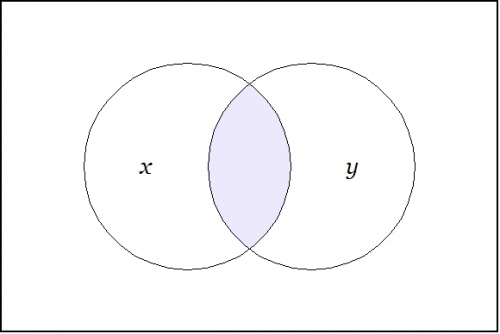
Back to the proposition \(xy.~\!\) Imagine yourself standing in a fixed cell of the corresponding venn diagram, say, the cell where the proposition \(xy\!\) is true, as shown here:

Now ask yourself: What is the value of the proposition \(xy\!\) at a distance of \(\operatorname{d}x\) and \(\operatorname{d}y\) from the cell \(xy\!\) where you are standing?

Don't think about it — just compute:

o---------------------------------------o | | | dx o o dy | | / \ / \ | | x o---@---o y | | | o---------------------------------------o | (x + dx) and (y + dy) | o---------------------------------------o

To make future graphs easier to draw in ASCII, I will use devices like @=@=@ and o=o=o to identify several nodes into one, as in this next redrawing:

o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | @=@ | | | o---------------------------------------o | (x + dx) and (y + dy) | o---------------------------------------o

However you draw it, these expressions follow because the expression \(x + \operatorname{d}x,\) where the plus sign indicates addition in \(\mathbb{B},\) that is, addition modulo 2, and thus corresponds to the exclusive disjunction operation in logic, parses to a graph of the following form:

o---------------------------------------o | | | x dx | | o---o | | \ / | | @ | | | o---------------------------------------o | x + dx | o---------------------------------------o

Next question: What is the difference between the value of the proposition \(xy\!\) "over there" and the value of the proposition \(xy\!\) where you are, all expressed as general formula, of course? Here 'tis:

o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ x y | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | ((x + dx) & (y + dy)) - xy | o---------------------------------------o

Oh, I forgot to mention: Computed over \(\mathbb{B},\) plus and minus are the very same operation. This will make the relationship between the differential and the integral parts of the resulting calculus slightly stranger than usual, but never mind that now.

Last question, for now: What is the value of this expression from your current standpoint, that is, evaluated at the point where \(xy\!\) is true? Well, substituting \(1\!\) for \(x\!\) and \(1\!\) for \(y\!\) in the graph amounts to the same thing as erasing those labels:

o---------------------------------------o | | | dx dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | ((1 + dx) & (1 + dy)) - 1·1 | o---------------------------------------o

And this is equivalent to the following graph:

o---------------------------------------o | | | dx dy | | o o | | \ / | | o | | | | | @ | | | o---------------------------------------o | dx or dy | o---------------------------------------o

Note 2

We have just met with the fact that the differential of the and is the or of the differentials.

\(x ~\operatorname{and}~ y \quad \xrightarrow{~\operatorname{Diff}~} \quad \operatorname{d}x ~\operatorname{or}~ \operatorname{d}y\)

o---------------------------------------o | | | dx dy | | o o | | \ / | | o | | x y | | | @ --Diff--> @ | | | o---------------------------------------o | x y --Diff--> ((dx)(dy)) | o---------------------------------------o

It will be necessary to develop a more refined analysis of that statement directly, but that is roughly the nub of it.

If the form of the above statement reminds you of De Morgan's rule, it is no accident, as differentiation and negation turn out to be closely related operations. Indeed, one can find discussions of logical difference calculus in the Boole–De Morgan correspondence and Peirce also made use of differential operators in a logical context, but the exploration of these ideas has been hampered by a number of factors, not the least of which being a syntax adequate to handle the complexity of expressions that evolve.

For my part, it was definitely a case of the calculus being smarter than the calculator thereof. The graphical pictures were catalytic in their power over my thinking process, leading me so quickly past so many obstructions that I did not have time to think about all of the difficulties that would otherwise have inhibited the derivation. It did eventually became necessary to write all this up in a linear script, and to deal with the various problems of interpretation and justification that I could imagine, but that took another 120 pages, and so, if you don't like this intuitive approach, then let that be your sufficient notice.

Let us run through the initial example again, this time attempting to interpret the formulas that develop at each stage along the way.

We begin with a proposition or a boolean function \(f(x, y) = xy.\!\)

A function like this has an abstract type and a concrete type. The abstract type is what we invoke when we write things like \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}\) or \(f : \mathbb{B}^2 \to \mathbb{B}.\) The concrete type takes into account the qualitative dimensions or the "units" of the case, which can be explained as follows.

Let \(X\!\) be the set of values \(\{ \texttt{(} x \texttt{)},~ x \} ~=~ \{ \operatorname{not}~ x,~ x \}.\)

Let \(Y\!\) be the set of values \(\{ \texttt{(} y \texttt{)},~ y \} ~=~ \{ \operatorname{not}~ y,~ y \}.\)

Then interpret the usual propositions about \(x, y\!\) as functions of the concrete type \(f : X \times Y \to \mathbb{B}.\)

We are going to consider various operators on these functions. Here, an operator \(\operatorname{F}\) is a function that takes one function \(f\!\) into another function \(\operatorname{F}f.\)

The first couple of operators that we need to consider are logical analogues of those that occur in the classical finite difference calculus, namely:

The difference operator \(\Delta,\!\) written here as \(\operatorname{D}.\)

The enlargement" operator \(\Epsilon,\!\) written here as \(\operatorname{E}.\)

These days, \(\operatorname{E}\) is more often called the shift operator.

In order to describe the universe in which these operators operate, it is necessary to enlarge the original universe of discourse, passing from the space \(U = X \times Y\) to its differential extension, \(\operatorname{E}U,\) that has the following description:

\(\operatorname{E}U ~=~ U \times \operatorname{d}U ~=~ X \times Y \times \operatorname{d}X \times \operatorname{d}Y,\)

with

\(\operatorname{d}X = \{ \texttt{(} \operatorname{d}x \texttt{)}, \operatorname{d}x \}\)  and  \(\operatorname{d}Y = \{ \texttt{(} \operatorname{d}y \texttt{)}, \operatorname{d}y \}.\)

The interpretations of these new symbols can be diverse, but the easiest option for now is just to say that \(\operatorname{d}x\) means "change \(x\!\)" and \(\operatorname{d}y\) means "change \(y\!\)". To draw the differential extension \(\operatorname{E}U\) of our present universe \(U = X \times Y\) as a venn diagram, it would take us four logical dimensions \(X, Y, \operatorname{d}X, \operatorname{d}Y,\) but we can project a suggestion of what it's about on the universe \(X \times Y\) by drawing arrows that cross designated borders, labeling the arrows as \(\operatorname{d}x\) when crossing the border between \(x\!\) and \(\texttt{(} x \texttt{)}\) and as \(\operatorname{d}y\) when crossing the border between \(y\!\) and \(\texttt{(} y \texttt{)},\) in either direction, in either case.

Propositions can be formed on differential variables, or any combination of ordinary logical variables and differential logical variables, in all the same ways that propositions can be formed on ordinary logical variables alone. For instance, the proposition \(\texttt{(} \operatorname{d}x \texttt{(} \operatorname{d}y \texttt{))}\) may be read to say that \(\operatorname{d}x \Rightarrow \operatorname{d}y,\) in other words, there is "no change in \(x\!\) without a change in \(y\!\)".

Given the proposition \(f(x, y)\!\) in \(U = X \times Y,\) the (first order) enlargement of \(f\!\) is the proposition \(\operatorname{E}f\) in \(\operatorname{E}U\) that is defined by the formula \(\operatorname{E}f(x, y, \operatorname{d}x, \operatorname{d}y) = f(x + \operatorname{d}x, y + \operatorname{d}y).\)

Applying the enlargement operator \(\operatorname{E}\) to the present example, \(f(x, y) = xy,\!\) we may compute the result as follows:

\(\operatorname{E}f(x, y, \operatorname{d}x, \operatorname{d}y) \quad = \quad (x + \operatorname{d}x)(y + \operatorname{d}y).\)

o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | @=@ | | | o---------------------------------------o | Ef = (x, dx) (y, dy) | o---------------------------------------o

Given the proposition \(f(x, y)\!\) in \(U = X \times Y,\) the (first order) difference of \(f\!\) is the proposition \(\operatorname{D}f\) in \(\operatorname{E}U\) that is defined by the formula \(\operatorname{D}f = \operatorname{E}f - f,\) that is, \(\operatorname{D}f(x, y, \operatorname{d}x, \operatorname{d}y) = f(x + \operatorname{d}x, y + \operatorname{d}y) - f(x, y).\)

In the example \(f(x, y) = xy,\!\) the result is:

\(\operatorname{D}f(x, y, \operatorname{d}x, \operatorname{d}y) \quad = \quad (x + \operatorname{d}x)(y + \operatorname{d}y) - xy.\)

o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ x y | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df = ((x, dx)(y, dy), xy) | o---------------------------------------o

We did not yet go through the trouble to interpret this (first order) difference of conjunction fully, but were happy simply to evaluate it with respect to a single location in the universe of discourse, namely, at the point picked out by the singular proposition \(xy,\!\) that is, at the place where \(x = 1\!\) and \(y = 1.\!\) This evaluation is written in the form \(\operatorname{D}f|_{xy}\) or \(\operatorname{D}f|_{(1, 1)},\) and we arrived at the locally applicable law that is stated and illustrated as follows:

\(f(x, y) ~=~ xy ~=~ x ~\operatorname{and}~ y \quad \Rightarrow \quad \operatorname{D}f|_{xy} ~=~ \texttt{((} \operatorname{dx} \texttt{)(} \operatorname{d}y \texttt{))} ~=~ \operatorname{d}x ~\operatorname{or}~ \operatorname{d}y.\)

The picture shows the analysis of the inclusive disjunction \(\texttt{((} \operatorname{d}x \texttt{)(} \operatorname{d}y \texttt{))}\) into the following exclusive disjunction:

\(\operatorname{d}x ~\texttt{(} \operatorname{d}y \texttt{)} ~+~ \operatorname{d}y ~\texttt{(} \operatorname{d}x \texttt{)} ~+~ \operatorname{d}x ~\operatorname{d}y.\)

This resulting differential proposition may be interpreted to say "change \(x\!\) or change \(y\!\) or both". And this can be recognized as just what you need to do if you happen to find yourself in the center cell and desire a detailed description of ways to depart it.

Note 3

Last time we computed what will variously be called the difference map, the difference proposition, or the local proposition \(\operatorname{D}f_p\) for the proposition \(f(x, y) = xy\!\) at the point \(p\!\) where \(x = 1\!\) and \(y = 1.\!\)

In the universe \(U = X \times Y,\) the four propositions \(xy,~ x\texttt{(}y\texttt{)},~ \texttt{(}x\texttt{)}y,~ \texttt{(}x\texttt{)(}y\texttt{)}\) that indicate the "cells", or the smallest regions of the venn diagram, are called singular propositions. These serve as an alternative notation for naming the points \((1, 1),~ (1, 0),~ (0, 1),~ (0, 0),\!\) respectively.

Thus we can write \(\operatorname{D}f_p = \operatorname{D}f|p = \operatorname{D}f|(1, 1) = \operatorname{D}f|xy,\) so long as we know the frame of reference in force.

Sticking with the example \(f(x, y) = xy,\!\) let us compute the value of the difference proposition \(\operatorname{D}f\) at all 4 points.

o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ x y | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df = ((x, dx)(y, dy), xy) | o---------------------------------------o

o---------------------------------------o | | | dx dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|xy = ((dx)(dy)) | o---------------------------------------o

o---------------------------------------o | | | o | | dx | dy | | o---o o---o | | \ | | / | | \ | | / o | | \| |/ | | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|x(y) = (dx) dy | o---------------------------------------o

o---------------------------------------o | | | o | | | dx dy | | o---o o---o | | \ | | / | | \ | | / o | | \| |/ | | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|(x)y = dx (dy) | o---------------------------------------o

o---------------------------------------o | | | o o | | | dx | dy | | o---o o---o | | \ | | / | | \ | | / o o | | \| |/ \ / | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|(x)(y) = dx dy | o---------------------------------------o

The easy way to visualize the values of these graphical expressions is just to notice the following equivalents:

o---------------------------------------o | | | x | | o-o-o-...-o-o-o | | \ / | | \ / | | \ / | | \ / x | | \ / o | | \ / | | | @ = @ | | | o---------------------------------------o | (x, , ... , , ) = (x) | o---------------------------------------o

o---------------------------------------o | | | o | | x_1 x_2 x_k | | | o---o-...-o---o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / x_1 ... x_k | | @ = @ | | | o---------------------------------------o | (x_1, ..., x_k, ()) = x_1 · ... · x_k | o---------------------------------------o

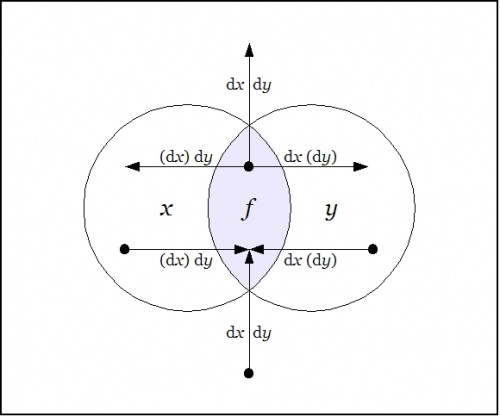
Laying out the arrows on the augmented venn diagram, one gets a picture of a differential vector field.

The Figure shows the points of the extended universe \(\operatorname{E}U = X \times Y \times \operatorname{d}X \times \operatorname{d}Y\) that satisfy the difference proposition \(\operatorname{D}f,\) namely, these:

\(\begin{array}{rcccc} 1. & x & y & \operatorname{d}x & \operatorname{d}y \\ 2. & x & y & \operatorname{d}x & (\operatorname{d}y) \\ 3. & x & y & (\operatorname{d}x) & \operatorname{d}y \\ 4. & x & (y) & (\operatorname{d}x) & \operatorname{d}y \\ 5. & (x) & y & \operatorname{d}x & (\operatorname{d}y) \\ 6. & (x) & (y) & \operatorname{d}x & \operatorname{d}y \end{array}\)

An inspection of these six points should make it easy to understand \(\operatorname{D}f\) as telling you what you have to do from each point of \(U\!\) in order to change the value borne by the proposition \(f(x, y).\!\)

Note 4

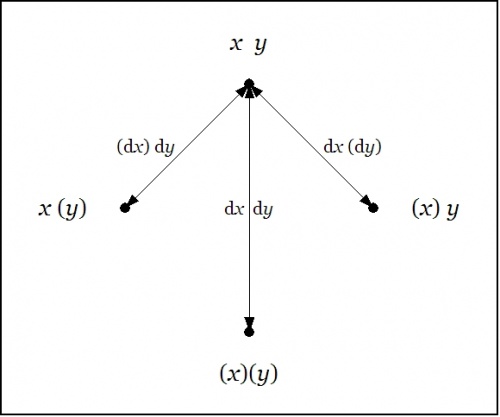
We have been studying the action of the difference operator \(\operatorname{D},\) also known as the localization operator, on the proposition \(f : X \times Y \to \mathbb{B}\) that is commonly known as the conjunction \(x \cdot y.\) We described \(\operatorname{D}f\) as a (first order) differential proposition, that is, a proposition of the type \(\operatorname{D}f : X \times Y \times \operatorname{d}X \times \operatorname{d}Y \to \mathbb{B}.\) Abstracting from the augmented venn diagram that illustrates how the models or satisfying interpretations of \(\operatorname{D}f\) distribute within the extended universe \(\operatorname{E}U = X \times Y \times \operatorname{d}X \times \operatorname{d}Y,\) we can depict \(\operatorname{D}f\) in the form of a digraph or directed graph, one whose points are labeled with the elements of \(U = X \times Y\) and whose arrows are labeled with the elements of \(\operatorname{d}U = \operatorname{d}X \times \operatorname{d}Y.\!\)

\(\begin{array}{rcccccc} f & = & x & \cdot & y \'"`UNIQ-MathJax1-QINU`"' Amazing! =='"`UNIQ--h-7--QINU`"'Note 8== We have been contemplating functions of the type \(f : U \to \mathbb{B}\) and studying the action of the operators \(\operatorname{E}\) and \(\operatorname{D}\) on this family. These functions, that we may identify for our present aims with propositions, inasmuch as they capture their abstract forms, are logical analogues of scalar potential fields. These are the sorts of fields that are so picturesquely presented in elementary calculus and physics textbooks by images of snow-covered hills and parties of skiers who trek down their slopes like least action heroes. The analogous scene in propositional logic presents us with forms more reminiscent of plateaunic idylls, being all plains at one of two levels, the mesas of verity and falsity, as it were, with nary a niche to inhabit between them, restricting our options for a sporting gradient of downhill dynamics to just one of two: standing still on level ground or falling off a bluff. We are still working well within the logical analogue of the classical finite difference calculus, taking in the novelties that the logical transmutation of familiar elements is able to bring to light. Soon we will take up several different notions of approximation relationships that may be seen to organize the space of propositions, and these will allow us to define several different forms of differential analysis applying to propositions. In time we will find reason to consider more general types of maps, having concrete types of the form \(X_1 \times \ldots \times X_k \to Y_1 \times \ldots \times Y_n\) and abstract types \(\mathbb{B}^k \to \mathbb{B}^n.\) We will think of these mappings as transforming universes of discourse into themselves or into others, in short, as transformations of discourse. Before we continue with this intinerary, however, I would like to highlight another sort of differential aspect that concerns the boundary operator or the marked connective that serves as one of the two basic connectives in the cactus language for ZOL. For example, consider the proposition \(f\!\) of concrete type \(f : X \times Y \times Z \to \mathbb{B}\) and abstract type \(f : \mathbb{B}^3 \to \mathbb{B}\) that is written \(\texttt{(} x, y, z \texttt{)}\) in cactus syntax. Taken as an assertion in what Peirce called the existential interpretation, \(\texttt{(} x, y, z \texttt{)}\) says that just one of \(x, y, z\!\) is false. It is useful to consider this assertion in relation to the conjunction \(xyz\!\) of the features that are engaged as its arguments. A venn diagram of \(\texttt{(} x, y, z \texttt{)}\) looks like this: In relation to the center cell indicated by the conjunction \(xyz,\!\) the region indicated by \(\texttt{(} x, y, z \texttt{)}\) is comprised of the adjacent or bordering cells. Thus they are the cells that are just across the boundary of the center cell, as if reached by way of Leibniz's minimal changes from the point of origin, here, \(xyz.\!\) The same sort of boundary relationship holds for any cell of origin that one chooses to indicate. One way to indicate a cell is by forming a logical conjunction of positive and negative basis features, that is, by constructing an expression of the form \(e_1 \cdot \ldots \cdot e_k,\) where \(e_j = x_j ~\text{or}~ e_j = \texttt{(} x_j \texttt{)},\) for \(j = 1 ~\text{to}~ k.\) The proposition \(\texttt{(} e_1, \ldots, e_k \texttt{)}\) indicates the disjunctive region consisting of the cells that are just next door to \(e_1 \cdot \ldots \cdot e_k.\) Note 9 Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object. — Charles Sanders Peirce, "Issues of Pragmaticism", [CP 5.438] One other subject that it would be opportune to mention at this point, while we have an object example of a mathematical group fresh in mind, is the relationship between the pragmatic maxim and what are commonly known in mathematics as representation principles. As it turns out, with regard to its formal characteristics, the pragmatic maxim unites the aspects of a representation principle with the attributes of what would ordinarily be known as a closure principle. We will consider the form of closure that is invoked by the pragmatic maxim on another occasion, focusing here and now on the topic of group representations. Let us return to the example of the four-group \(V_4.\!\) We encountered this group in one of its concrete representations, namely, as a transformation group that acts on a set of objects, in this case a set of sixteen functions or propositions. Forgetting about the set of objects that the group transforms among themselves, we may take the abstract view of the group's operational structure, for example, in the form of the group operation table copied here: \(\cdot\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{e}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{f}\) \(\operatorname{f}\) \(\operatorname{e}\) \(\operatorname{h}\) \(\operatorname{g}\) \(\operatorname{g}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{h}\) \(\operatorname{h}\) \(\operatorname{g}\) \(\operatorname{f}\) \(\operatorname{e}\) This operation table is abstractly the same as, or isomorphic to, the versions with the \(\operatorname{E}_{ij}\) operators and the \(\operatorname{T}_{ij}\) transformations that we discussed earlier. That is to say, the story is the same — only the names have been changed. An abstract group can have a multitude of significantly and superficially different representations. Even after we have long forgotten the details of the particular representation that we may have come in with, there are species of concrete representations, called the regular representations, that are always readily available, as they can be generated from the mere data of the abstract operation table itself. To see how a regular representation is constructed from the abstract operation table, pick a group element at the top of the table and "consider its effects" on each of the group elements listed on the left. These effects may be recorded in one of the ways that Peirce often used, as a logical aggregate of elementary dyadic relatives, that is, as a logical disjunction or sum whose terms represent the \(\operatorname{input} : \operatorname{output}\) pairs that are produced by each group element in turn. This forms one of the two possible regular representations of the group, specifically, the one that is called the post-regular representation or the right regular representation. It has long been conventional to organize the terms of this logical sum in the form of a matrix: Reading "\(+\!\)" as a logical disjunction: \(\begin{matrix} \operatorname{G} & = & \operatorname{e} & + & \operatorname{f} & + & \operatorname{g} & + & \operatorname{h} \end{matrix}\) And so, by expanding effects, we get: \(\begin{matrix} \operatorname{G} & = & \operatorname{e}:\operatorname{e} & + & \operatorname{f}:\operatorname{f} & + & \operatorname{g}:\operatorname{g} & + & \operatorname{h}:\operatorname{h} \'"`UNIQ-MathJax2-QINU`"' is the relate, \(J\!\) is the correlate, and in our current example we read \(I:J,\!\) or more exactly, \(\mathit{n}_{ij} = 1,\!\) to say that \(I\!\) is a noder of \(J.\!\) This is the mode of reading that we call multiplying on the left. In the algebraic, permutational, or transformational contexts of application, however, Peirce converts to the alternative mode of reading, although still calling \(I\!\) the relate and \(J\!\) the correlate, the elementary relative \(I:J\!\) now means that \(I\!\) gets changed into \(J.\!\) In this scheme of reading, the transformation \(\mathrm{A}\!:\!\mathrm{B} + \mathrm{B}\!:\!\mathrm{C} + \mathrm{C}\!:\!\mathrm{A}\) is a permutation of the aggregate \(\mathbf{1} = \mathrm{A} + \mathrm{B} + \mathrm{C},\) or what we would now call the set \(\{ \mathrm{A}, \mathrm{B}, \mathrm{C} \},\!\) in particular, it is the permutation that is otherwise notated as follows: \(\begin{Bmatrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\ \mathrm{B} & \mathrm{C} & \mathrm{A} \end{Bmatrix}\) This is consistent with the convention that Peirce uses in the paper "On a Class of Multiple Algebras" (CP 3.324–327). Note 16 We have been contemplating the virtues and the utilities of the pragmatic maxim as a hermeneutic heuristic, specifically, as a principle of interpretation that guides us in finding a clarifying representation for a problematic corpus of symbols in terms of their actions on other symbols or their effects on the syntactic contexts in which we conceive to distribute them. I started off considering the regular representations of groups as constituting what appears to be one of the simplest possible applications of this overall principle of representation. There are a few problems of implementation that have to be worked out in practice, most of which are cleared up by keeping in mind which of several possible conventions we have chosen to follow at a given time. But there does appear to remain this rather more substantial question: Are the effects we seek relates or correlates, or does it even matter? I will have to leave that question as it is for now, in hopes that a solution will evolve itself in time. Note 17 There a big reasons and little reasons for caring about this humble example. The little reasons we find all under our feet. One big reason I can now quite blazonly enounce in the fashion of this not so subtle subtitle: Obstacles to Applying the Pragmatic Maxim No sooner do you get a good idea and try to apply it than you find that a motley array of obstacles arise. It seems as if I am constantly lamenting the fact these days that people, and even admitted Peircean persons, do not in practice more consistently apply the maxim of pragmatism to the purpose for which it is purportedly intended by its author. That would be the clarification of concepts, or intellectual symbols, to the point where their inherent senses, or their lacks thereof, would be rendered manifest to all and sundry interpreters. There are big obstacles and little obstacles to applying the pragmatic maxim. In good subgoaling fashion, I will merely mention a few of the bigger blocks, as if in passing, and then get down to the devilish details that immediately obstruct our way. Obstacle 1 People do not always read the instructions very carefully. There is a tendency in readers of particular prior persuasions to blow the problem all out of proportion, to think that the maxim is meant to reveal the absolutely positive and the totally unique meaning of every preconception to which they might deign or elect to apply it. Reading the maxim with an even minimal attention, you can see that it promises no such finality of unindexed sense, but ties what you conceive to you. I have lately come to wonder at the tenacity of this misinterpretation. Perhaps people reckon that nothing less would be worth their attention. I am not sure. I can only say the achievement of more modest goals is the sort of thing on which our daily life depends, and there can be no final end to inquiry nor any ultimate community without a continuation of life, and that means life on a day to day basis. All of which only brings me back to the point of persisting with local meantime examples, because if we can't apply the maxim there, we can't apply it anywhere. And now I need to go out of doors and weed my garden for a time … Note 18 Obstacles to Applying the Pragmatic Maxim Obstacle 2 Applying the pragmatic maxim, even with a moderate aim, can be hard. I think that my present example, deliberately impoverished as it is, affords us with an embarrassing richness of evidence of just how complex the simple can be. All the better reason for me to see if I can finish it up before moving on. Expressed most simply, the idea is to replace the question of what it is, which modest people know is far too difficult for them to answer right off, with the question of what it does, which most of us know a modicum about. In the case of regular representations of groups we found a non-plussing surplus of answers to sort our way through. So let us track back one more time to see if we can learn any lessons that might carry over to more realistic cases. Here is is the operation table of \(V_4\!\) once again: \(\text{Klein Four-Group}~ V_4\) \(\cdot\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{e}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{f}\) \(\operatorname{f}\) \(\operatorname{e}\) \(\operatorname{h}\) \(\operatorname{g}\) \(\operatorname{g}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{h}\) \(\operatorname{h}\) \(\operatorname{g}\) \(\operatorname{f}\) \(\operatorname{e}\) A group operation table is really just a device for recording a certain 3-adic relation, to be specific, the set of triples of the form \((x, y, z)\!\) satisfying the equation \(x \cdot y = z.\) In the case of \(V_4 = (G, \cdot),\) where \(G\!\) is the underlying set \(\{ \operatorname{e}, \operatorname{f}, \operatorname{g}, \operatorname{h} \},\) we have the 3-adic relation \(L(V_4) \subseteq G \times G \times G\) whose triples are listed below: \(\begin{matrix} (\mathrm{e}, \mathrm{e}, \mathrm{e}) & (\mathrm{e}, \mathrm{f}, \mathrm{f}) & (\mathrm{e}, \mathrm{g}, \mathrm{g}) & (\mathrm{e}, \mathrm{h}, \mathrm{h}) \\[6pt] (\mathrm{f}, \mathrm{e}, \mathrm{f}) & (\mathrm{f}, \mathrm{f}, \mathrm{e}) & (\mathrm{f}, \mathrm{g}, \mathrm{h}) & (\mathrm{f}, \mathrm{h}, \mathrm{g}) \\[6pt] (\mathrm{g}, \mathrm{e}, \mathrm{g}) & (\mathrm{g}, \mathrm{f}, \mathrm{h}) & (\mathrm{g}, \mathrm{g}, \mathrm{e}) & (\mathrm{g}, \mathrm{h}, \mathrm{f}) \\[6pt] (\mathrm{h}, \mathrm{e}, \mathrm{h}) & (\mathrm{h}, \mathrm{f}, \mathrm{g}) & (\mathrm{h}, \mathrm{g}, \mathrm{f}) & (\mathrm{h}, \mathrm{h}, \mathrm{e}) \end{matrix}\) It is part of the definition of a group that the 3-adic relation \(L \subseteq G^3\) is actually a function \(L : G \times G \to G.\) It is from this functional perspective that we can see an easy way to derive the two regular representations. Since we have a function of the type \(L : G \times G \to G,\) we can define a couple of substitution operators: 1. \(\operatorname{Sub}(x, (\underline{~~}, y))\) puts any specified \(x\!\) into the empty slot of the rheme \((\underline{~~}, y),\) with the effect of producing the saturated rheme \((x, y)\!\) that evaluates to \(x \cdot y.\) 2. \(\operatorname{Sub}(x, (y, \underline{~~}))\) puts any specified \(x\!\) into the empty slot of the rheme \((y, \underline{~~}),\) with the effect of producing the saturated rheme \((y, x)\!\) that evaluates to \(y \cdot x.\) In (1) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((\underline{~~}, y),\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((\underline{~~}, y)\) into \(x \cdot y,\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : x \cdot y) ~|~ y \in G \}.\) The pairs \((y : x \cdot y)\) can be found by picking an \(x\!\) from the left margin of the group operation table and considering its effects on each \(y\!\) in turn as these run across the top margin. This aspect of pragmatic definition we recognize as the regular ante-representation: \(\begin{matrix} \mathrm{e} & = & \mathrm{e}:\mathrm{e} & + & \mathrm{f}:\mathrm{f} & + & \mathrm{g}:\mathrm{g} & + & \mathrm{h}:\mathrm{h} \\[4pt] \mathrm{f} & = & \mathrm{e}:\mathrm{f} & + & \mathrm{f}:\mathrm{e} & + & \mathrm{g}:\mathrm{h} & + & \mathrm{h}:\mathrm{g} \\[4pt] \mathrm{g} & = & \mathrm{e}:\mathrm{g} & + & \mathrm{f}:\mathrm{h} & + & \mathrm{g}:\mathrm{e} & + & \mathrm{h}:\mathrm{f} \\[4pt] \mathrm{h} & = & \mathrm{e}:\mathrm{h} & + & \mathrm{f}:\mathrm{g} & + & \mathrm{g}:\mathrm{f} & + & \mathrm{h}:\mathrm{e} \end{matrix}\) In (2) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((y, \underline{~~}),\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((y, \underline{~~})\) into \(y \cdot x,\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : y \cdot x) ~|~ y \in G \}.\) The pairs \((y : y \cdot x)\) can be found by picking an \(x\!\) from the top margin of the group operation table and considering its effects on each \(y\!\) in turn as these run down the left margin. This aspect of pragmatic definition we recognize as the regular post-representation: \(\begin{matrix} \mathrm{e} & = & \mathrm{e}:\mathrm{e} & + & \mathrm{f}:\mathrm{f} & + & \mathrm{g}:\mathrm{g} & + & \mathrm{h}:\mathrm{h} \\[4pt] \mathrm{f} & = & \mathrm{e}:\mathrm{f} & + & \mathrm{f}:\mathrm{e} & + & \mathrm{g}:\mathrm{h} & + & \mathrm{h}:\mathrm{g} \\[4pt] \mathrm{g} & = & \mathrm{e}:\mathrm{g} & + & \mathrm{f}:\mathrm{h} & + & \mathrm{g}:\mathrm{e} & + & \mathrm{h}:\mathrm{f} \\[4pt] \mathrm{h} & = & \mathrm{e}:\mathrm{h} & + & \mathrm{f}:\mathrm{g} & + & \mathrm{g}:\mathrm{f} & + & \mathrm{h}:\mathrm{e} \end{matrix}\) If the ante-rep looks the same as the post-rep, now that I'm writing them in the same dialect, that is because \(V_4\!\) is abelian (commutative), and so the two representations have the very same effects on each point of their bearing. Note 19 So long as we're in the neighborhood, we might as well take in some more of the sights, for instance, the smallest example of a non-abelian (non-commutative) group. This is a group of six elements, say, \(G = \{ \operatorname{e}, \operatorname{f}, \operatorname{g}, \operatorname{h}, \operatorname{i}, \operatorname{j} \},\!\) with no relation to any other employment of these six symbols being implied, of course, and it can be most easily represented as the permutation group on a set of three letters, say, \(X = \{ A, B, C \},\!\) usually notated as \(G = \operatorname{Sym}(X)\) or more abstractly and briefly, as \(\operatorname{Sym}(3)\) or \(S_3.\!\) The next Table shows the intended correspondence between abstract group elements and the permutation or substitution operations in \(\operatorname{Sym}(X).\) \(\text{Permutation Substitutions in}~ \operatorname{Sym} \{ \mathrm{A}, \mathrm{B}, \mathrm{C} \}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{i}\) \(\operatorname{j}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{A} & \mathrm{B} & \mathrm{C} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{C} & \mathrm{A} & \mathrm{B} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{B} & \mathrm{C} & \mathrm{A} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{A} & \mathrm{C} & \mathrm{B} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{C} & \mathrm{B} & \mathrm{A} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{B} & \mathrm{A} & \mathrm{C} \end{matrix}\) Here is the operation table for \(S_3,\!\) given in abstract fashion: Symmetric Group S_3 o-------------------------------------------------o | | | ^ | | e / \ e | | / \ | | / e \ | | f / \ / \ f | | / \ / \ | | / f \ f \ | | g / \ / \ / \ g | | / \ / \ / \ | | / g \ g \ g \ | | h / \ / \ / \ / \ h | | / \ / \ / \ / \ | | / h \ e \ e \ h \ | | i / \ / \ / \ / \ / \ i | | / \ / \ / \ / \ / \ | | / i \ i \ f \ j \ i \ | | j / \ / \ / \ / \ / \ / \ j | | / \ / \ / \ / \ / \ / \ | | ( j \ j \ j \ i \ h \ j ) | | \ / \ / \ / \ / \ / \ / | | \ / \ / \ / \ / \ / \ / | | \ h \ h \ e \ j \ i / | | \ / \ / \ / \ / \ / | | \ / \ / \ / \ / \ / | | \ i \ g \ f \ h / | | \ / \ / \ / \ / | | \ / \ / \ / \ / | | \ f \ e \ g / | | \ / \ / \ / | | \ / \ / \ / | | \ g \ f / | | \ / \ / | | \ / \ / | | \ e / | | \ / | | \ / | | v | | | o-------------------------------------------------o By the way, we will meet with the symmetric group \(S_3\!\) again when we return to take up the study of Peirce's early paper "On a Class of Multiple Algebras" (CP 3.324–327), and also his late unpublished work "The Simplest Mathematics" (1902) (CP 4.227–323), with particular reference to the section that treats of "Trichotomic Mathematics" (CP 4.307–323). Note 20 By way of collecting a short-term pay-off for all the work — not to mention all the peirce-spiration — that we sweated out over the regular representations of the Klein 4-group \(V_4,\!\) let us write out as quickly as possible in relative form a minimal budget of representations of the symmetric group on three letters, \(S_3 = \operatorname{Sym}(3).\) After doing the usual bit of compare and contrast among these divers representations, we will have enough concrete material beneath our abstract belts to tackle a few of the presently obscur'd details of Peirce's early "Algebra + Logic" papers. \(\text{Permutation Substitutions in}~ \operatorname{Sym} \{ \mathrm{A}, \mathrm{B}, \mathrm{C} \}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{i}\) \(\operatorname{j}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{A} & \mathrm{B} & \mathrm{C} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{C} & \mathrm{A} & \mathrm{B} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{B} & \mathrm{C} & \mathrm{A} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{A} & \mathrm{C} & \mathrm{B} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{C} & \mathrm{B} & \mathrm{A} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{B} & \mathrm{A} & \mathrm{C} \end{matrix}\) Writing this table in relative form generates the following natural representation of \(S_3.\!\) \(\begin{matrix} \operatorname{e} & = & \operatorname{A}\!:\!\operatorname{A} & + & \operatorname{B}\!:\!\operatorname{B} & + & \operatorname{C}\!:\!\operatorname{C} \\[4pt] \operatorname{f} & = & \operatorname{A}\!:\!\operatorname{C} & + & \operatorname{B}\!:\!\operatorname{A} & + & \operatorname{C}\!:\!\operatorname{B} \\[4pt] \operatorname{g} & = & \operatorname{A}\!:\!\operatorname{B} & + & \operatorname{B}\!:\!\operatorname{C} & + & \operatorname{C}\!:\!\operatorname{A} \\[4pt] \operatorname{h} & = & \operatorname{A}\!:\!\operatorname{A} & + & \operatorname{B}\!:\!\operatorname{C} & + & \operatorname{C}\!:\!\operatorname{B} \\[4pt] \operatorname{i} & = & \operatorname{A}\!:\!\operatorname{C} & + & \operatorname{B}\!:\!\operatorname{B} & + & \operatorname{C}\!:\!\operatorname{A} \\[4pt] \operatorname{j} & = & \operatorname{A}\!:\!\operatorname{B} & + & \operatorname{B}\!:\!\operatorname{A} & + & \operatorname{C}\!:\!\operatorname{C} \end{matrix}\) I have without stopping to think about it written out this natural representation of \(S_3\!\) in the style that comes most naturally to me, to wit, the "right" way, whereby an ordered pair configured as \(X:Y\!\) constitutes the turning of \(X\!\) into \(Y.\!\) It is possible that the next time we check in with CSP that we will have to adjust our sense of direction, but that will be an easy enough bridge to cross when we come to it. Note 21 To construct the regular representations of \(S_3,\!\) we begin with the data of its operation table: Symmetric Group S_3 o-------------------------------------------------o | | | ^ | | e / \ e | | / \ | | / e \ | | f / \ / \ f | | / \ / \ | | / f \ f \ | | g / \ / \ / \ g | | / \ / \ / \ | | / g \ g \ g \ | | h / \ / \ / \ / \ h | | / \ / \ / \ / \ | | / h \ e \ e \ h \ | | i / \ / \ / \ / \ / \ i | | / \ / \ / \ / \ / \ | | / i \ i \ f \ j \ i \ | | j / \ / \ / \ / \ / \ / \ j | | / \ / \ / \ / \ / \ / \ | | ( j \ j \ j \ i \ h \ j ) | | \ / \ / \ / \ / \ / \ / | | \ / \ / \ / \ / \ / \ / | | \ h \ h \ e \ j \ i / | | \ / \ / \ / \ / \ / | | \ / \ / \ / \ / \ / | | \ i \ g \ f \ h / | | \ / \ / \ / \ / | | \ / \ / \ / \ / | | \ f \ e \ g / | | \ / \ / \ / | | \ / \ / \ / | | \ g \ f / | | \ / \ / | | \ / \ / | | \ e / | | \ / | | \ / | | v | | | o-------------------------------------------------o Just by way of staying clear about what we are doing, let's return to the recipe that we worked out before: It is part of the definition of a group that the 3-adic relation \(L \subseteq G^3\) is actually a function \(L : G \times G \to G.\) It is from this functional perspective that we can see an easy way to derive the two regular representations. Since we have a function of the type \(L : G \times G \to G,\) we can define a couple of substitution operators: 1. \(\operatorname{Sub}(x, (\underline{~~}, y))\) puts any specified \(x\!\) into the empty slot of the rheme \((\underline{~~}, y),\) with the effect of producing the saturated rheme \((x, y)\!\) that evaluates to \(x \cdot y.\) 2. \(\operatorname{Sub}(x, (y, \underline{~~}))\) puts any specified \(x\!\) into the empty slot of the rheme \((y, \underline{~~}),\) with the effect of producing the saturated rheme \((y, x)\!\) that evaluates to \(y \cdot x.\) In (1) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((\underline{~~}, y),\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((\underline{~~}, y)\) into \(x \cdot y,\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : x \cdot y) ~|~ y \in G \}.\) The pairs \((y : x \cdot y)\) can be found by picking an \(x\!\) from the left margin of the group operation table and considering its effects on each \(y\!\) in turn as these run along the right margin. This produces the regular ante-representation of \(S_3,\!\) like so: \(\begin{array}{*{13}{c}} \operatorname{e} & = & \operatorname{e}:\operatorname{e} & + & \operatorname{f}:\operatorname{f} & + & \operatorname{g}:\operatorname{g} & + & \operatorname{h}:\operatorname{h} & + & \operatorname{i}:\operatorname{i} & + & \operatorname{j}:\operatorname{j} \\[4pt] \operatorname{f} & = & \operatorname{e}:\operatorname{f} & + & \operatorname{f}:\operatorname{g} & + & \operatorname{g}:\operatorname{e} & + & \operatorname{h}:\operatorname{j} & + & \operatorname{i}:\operatorname{h} & + & \operatorname{j}:\operatorname{i} \\[4pt] \operatorname{g} & = & \operatorname{e}:\operatorname{g} & + & \operatorname{f}:\operatorname{e} & + & \operatorname{g}:\operatorname{f} & + & \operatorname{h}:\operatorname{i} & + & \operatorname{i}:\operatorname{j} & + & \operatorname{j}:\operatorname{h} \\[4pt] \operatorname{h} & = & \operatorname{e}:\operatorname{h} & + & \operatorname{f}:\operatorname{i} & + & \operatorname{g}:\operatorname{j} & + & \operatorname{h}:\operatorname{e} & + & \operatorname{i}:\operatorname{f} & + & \operatorname{j}:\operatorname{g} \\[4pt] \operatorname{i} & = & \operatorname{e}:\operatorname{i} & + & \operatorname{f}:\operatorname{j} & + & \operatorname{g}:\operatorname{h} & + & \operatorname{h}:\operatorname{g} & + & \operatorname{i}:\operatorname{e} & + & \operatorname{j}:\operatorname{f} \\[4pt] \operatorname{j} & = & \operatorname{e}:\operatorname{j} & + & \operatorname{f}:\operatorname{h} & + & \operatorname{g}:\operatorname{i} & + & \operatorname{h}:\operatorname{f} & + & \operatorname{i}:\operatorname{g} & + & \operatorname{j}:\operatorname{e} \end{array}\) In (2) we consider the effects of each \(x\!\) in its practical bearing on contexts of the form \((y, \underline{~~}),\) as \(y\!\) ranges over \(G,\!\) and the effects are such that \(x\!\) takes \((y, \underline{~~})\) into \(y \cdot x,\) for \(y\!\) in \(G,\!\) all of which is notated as \(x = \{ (y : y \cdot x) ~|~ y \in G \}.\) The pairs \((y : y \cdot x)\) can be found by picking an \(x\!\) on the right margin of the group operation table and considering its effects on each \(y\!\) in turn as these run along the left margin. This generates the regular post-representation of \(S_3,\!\) like so: \(\begin{array}{*{13}{c}} \operatorname{e} & = & \operatorname{e}:\operatorname{e} & + & \operatorname{f}:\operatorname{f} & + & \operatorname{g}:\operatorname{g} & + & \operatorname{h}:\operatorname{h} & + & \operatorname{i}:\operatorname{i} & + & \operatorname{j}:\operatorname{j} \\[4pt] \operatorname{f} & = & \operatorname{e}:\operatorname{f} & + & \operatorname{f}:\operatorname{g} & + & \operatorname{g}:\operatorname{e} & + & \operatorname{h}:\operatorname{i} & + & \operatorname{i}:\operatorname{j} & + & \operatorname{j}:\operatorname{h} \\[4pt] \operatorname{g} & = & \operatorname{e}:\operatorname{g} & + & \operatorname{f}:\operatorname{e} & + & \operatorname{g}:\operatorname{f} & + & \operatorname{h}:\operatorname{j} & + & \operatorname{i}:\operatorname{h} & + & \operatorname{j}:\operatorname{i} \\[4pt] \operatorname{h} & = & \operatorname{e}:\operatorname{h} & + & \operatorname{f}:\operatorname{j} & + & \operatorname{g}:\operatorname{i} & + & \operatorname{h}:\operatorname{e} & + & \operatorname{i}:\operatorname{g} & + & \operatorname{j}:\operatorname{f} \\[4pt] \operatorname{i} & = & \operatorname{e}:\operatorname{i} & + & \operatorname{f}:\operatorname{h} & + & \operatorname{g}:\operatorname{j} & + & \operatorname{h}:\operatorname{f} & + & \operatorname{i}:\operatorname{e} & + & \operatorname{j}:\operatorname{g} \\[4pt] \operatorname{j} & = & \operatorname{e}:\operatorname{j} & + & \operatorname{f}:\operatorname{i} & + & \operatorname{g}:\operatorname{h} & + & \operatorname{h}:\operatorname{g} & + & \operatorname{i}:\operatorname{f} & + & \operatorname{j}:\operatorname{e} \end{array}\) If the ante-rep looks different from the post-rep, it is just as it should be, as \(S_3\!\) is non-abelian (non-commutative), and so the two representations differ in the details of their practical effects, though, of course, being representations of the same abstract group, they must be isomorphic. Note 22   the way of heaven and earth is to be long continued in their operation without stopping   — i ching, hexagram 32 You may be wondering what happened to the announced subject of Differential Logic, and if you think that we have been taking a slight excursion — to use my favorite euphemism for digression — my reply to the charge of a scenic rout would need to be both "yes and no". What happened was this. At the sign-post marked by Sigil 7, we made the observation that the shift operators \(\operatorname{E}_{ij}\!\) form a transformation group that acts on the propositions of the form \(f : \mathbb{B}^2 \to \mathbb{B}.\) Now group theory is a very attractive subject, but it did not really have the effect of drawing us so far off our initial course as you may at first think. For one thing, groups, in particular, the groups that have come to be named after the Norwegian mathematician Marius Sophus Lie, have turned out to be of critical utility in the solution of differential equations. For another thing, group operations afford us examples of triadic relations that have been extremely well-studied over the years, and this provides us with quite a bit of guidance in the study of sign relations, another class of triadic relations of significance for logical studies, in our brief acquaintance with which we have scarcely even started to break the ice. Finally, I could hardly avoid taking up the connection between group representations, a very generic class of logical models, and the all-important pragmatic maxim. Biographical Data for Marius Sophus Lie (1842–1899) Note 23   Bein' on the twenty-third of June,         As I sat weaving all at my loom, Bein' on the twenty-third of June,         As I sat weaving all at my loom, I heard a thrush, singing on yon bush,         And the song she sang was The Jug of Punch. We've seen a couple of groups, \(V_4\!\) and \(S_3,\!\) represented in various ways, and we've seen their representations presented in a variety of different manners. Let us look at one other stylistic variant for presenting a representation that is frequently seen, the so-called matrix representation of a group. Recalling the manner of our acquaintance with the symmetric group \(S_3,\!\) we began with the bigraph (bipartite graph) picture of its natural representation as the set of all permutations or substitutions on the set \(X = \{ \mathrm{A}, \mathrm{B}, \mathrm{C} \}.\!\) \(\text{Permutation Substitutions in}~ \operatorname{Sym} \{ \mathrm{A}, \mathrm{B}, \mathrm{C} \}\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{i}\) \(\operatorname{j}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{A} & \mathrm{B} & \mathrm{C} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{C} & \mathrm{A} & \mathrm{B} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{B} & \mathrm{C} & \mathrm{A} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{A} & \mathrm{C} & \mathrm{B} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{C} & \mathrm{B} & \mathrm{A} \end{matrix}\) \(\begin{matrix} \mathrm{A} & \mathrm{B} & \mathrm{C} \\[3pt] \downarrow & \downarrow & \downarrow \\[6pt] \mathrm{B} & \mathrm{A} & \mathrm{C} \end{matrix}\) Then we rewrote these permutations — being functions \(f : X \to X\) they can also be recognized as being 2-adic relations \(f \subseteq X \times X\) — in relative form, in effect, in the manner to which Peirce would have made us accustomed had he been given a relative half-a-chance: \(\begin{matrix} \operatorname{e} & = & \mathrm{A}\!:\!\mathrm{A} & + & \mathrm{B}\!:\!\mathrm{B} & + & \mathrm{C}\!:\!\mathrm{C} \\[4pt] \operatorname{f} & = & \mathrm{A}\!:\!\mathrm{C} & + & \mathrm{B}\!:\!\mathrm{A} & + & \mathrm{C}\!:\!\mathrm{B} \\[4pt] \operatorname{g} & = & \mathrm{A}\!:\!\mathrm{B} & + & \mathrm{B}\!:\!\mathrm{C} & + & \mathrm{C}\!:\!\mathrm{A} \\[4pt] \operatorname{h} & = & \mathrm{A}\!:\!\mathrm{A} & + & \mathrm{B}\!:\!\mathrm{C} & + & \mathrm{C}\!:\!\mathrm{B} \\[4pt] \operatorname{i} & = & \mathrm{A}\!:\!\mathrm{C} & + & \mathrm{B}\!:\!\mathrm{B} & + & \mathrm{C}\!:\!\mathrm{A} \\[4pt] \operatorname{j} & = & \mathrm{A}\!:\!\mathrm{B} & + & \mathrm{B}\!:\!\mathrm{A} & + & \mathrm{C}\!:\!\mathrm{C} \end{matrix}\) These days one is much more likely to encounter the natural representation of \(S_3\!\) in the form of a linear representation, that is, as a family of linear transformations that map the elements of a suitable vector space into each other, all of which would in turn usually be represented by a set of matrices like these: \(\text{Matrix Representations of Permutations in}~ \operatorname{Sym}(3)\) \(\operatorname{e}\) \(\operatorname{f}\) \(\operatorname{g}\) \(\operatorname{h}\) \(\operatorname{i}\) \(\operatorname{j}\) \(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\) \(\begin{matrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix}\) \(\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}\) \(\begin{matrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{matrix}\) \(\begin{matrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}\) \(\begin{matrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{matrix}\) The key to the mysteries of these matrices is revealed by noting that their coefficient entries are arrayed and overlaid on a place-mat marked like so: \(\begin{bmatrix} \mathrm{A}\!:\!\mathrm{A} & \mathrm{A}\!:\!\mathrm{B} & \mathrm{A}\!:\!\mathrm{C} \\ \mathrm{B}\!:\!\mathrm{A} & \mathrm{B}\!:\!\mathrm{B} & \mathrm{B}\!:\!\mathrm{C} \\ \mathrm{C}\!:\!\mathrm{A} & \mathrm{C}\!:\!\mathrm{B} & \mathrm{C}\!:\!\mathrm{C} \end{bmatrix}\) Of course, the place-settings of convenience at different symposia may vary. Note 24   In the beginning was the three-pointed star, One smile of light across the empty face; One bough of bone across the rooting air, The substance forked that marrowed the first sun; And, burning ciphers on the round of space, Heaven and hell mixed as they spun.   — Dylan Thomas, "In The Beginning", Verse 1 I'm afrayed that this thread is just bound to keep encountering its manifold of tensuous distractions, but I'd like to try and return now to the topic of inquiry, espectrally viewed in differential aspect. Here's one picture of how it begins, one angle on the point of departure: o-----------------------------------------------------------o | | | | | o-------------o | | / \ | | / \ | | / \ | | / \ | | / \ | | o o | | | | | | | | | | | Observation | | | | | | | | | | | o--o----------o o----------o--o | | / \ \ / / \ | | / \ d_I ^ o ^ d_E / \ | | / \ \/ \/ / \ | | / \ /\ /\ / \ | | / \ / @ \ / \ | | o o--o---|---o--o o | | | | | | | | | | | v | | | | | Expectation | d_O | Intention | | | | | | | | | | | | | | | o o o o | | \ \ / / | | \ \ / / | | \ \ / / | | \ o / | | \ / \ / | | o-------------o o-------------o | | | | | o-----------------------------------------------------------o From what we must assume was a state of Unconscious Nirvana (UN), since we do not acutely become conscious until after we are exiled from that garden of our blissful innocence, where our Expectations, our Intentions, our Observations all subsist in a state of perfect harmony, one with every barely perceived other, something intrudes on that scene of paradise to knock us out of that blessed isle and to trouble our countenance forever after at the retrospect thereof. The least disturbance, it being provident and prudent both to take that first up, will arise in just one of three ways, in accord with the mode of discord that importunes on our equanimity, whether it is Expectation, Intention, Observation that incipiently incites the riot, departing as it will from congruence with the other two modes of being. In short, we cross just one of the three lines that border on the center, or perhaps it is better to say that the objective situation transits one of the chordal bounds of harmony, for the moment marked as \(\operatorname{d}_E, \operatorname{d}_I, \operatorname{d}_O\) to note the fact one's Expectation, Intention, Observation, respectively, is the mode that we duly indite as the one that's sounding the sour note. A difference between Expectation and Observation is experienced as a Surprise, a phenomenon that calls for an Explanation. A discrepancy between Intention and Observation is experienced as a Problem, a situation that calls for a Plan of Action. A disparity between Expectation and Intention has no obvious name — I remember once thinking of a term that I thought was apt at the time, but I can't recall what it was, nor find the notes where I recorded it. At any rate, the modes of experiencing a surprising phenomenon or a problematic situation, as described just now, are already complex modalities, and will need to be analyzed further if we want to relate them to the minimal changes \(\operatorname{d}_E, \operatorname{d}_I, \operatorname{d}_O.\) Let me think about that for a little while and see what transpires. Note 25   In the beginning was the pale signature, Three-syllabled and starry as the smile; And after came the imprints on the water, Stamp of the minted face upon the moon; The blood that touched the crosstree and the grail Touched the first cloud and left a sign.   — Dylan Thomas, "In The Beginning", Verse 2 Note 26   In the beginning was the mounting fire That set alight the weathers from a spark, A three-eyed, red-eyed spark, blunt as a flower; Life rose and spouted from the rolling seas, Burst in the roots, pumped from the earth and rock The secret oils that drive the grass.   — Dylan Thomas, "In The Beginning", Verse 3 Document History Ontology List (Apr–Jul 2002) http://web.archive.org/web/20110612002240/http://suo.ieee.org/ontology/thrd28.html#04040 http://web.archive.org/web/20140406040004/http://suo.ieee.org/ontology/msg04040.html http://web.archive.org/web/20110612001949/http://suo.ieee.org/ontology/msg04041.html http://web.archive.org/web/20110612010502/http://suo.ieee.org/ontology/msg04045.html http://web.archive.org/web/20110612005212/http://suo.ieee.org/ontology/msg04046.html http://web.archive.org/web/20110612001954/http://suo.ieee.org/ontology/msg04047.html http://web.archive.org/web/20110612010620/http://suo.ieee.org/ontology/msg04048.html http://web.archive.org/web/20110612010550/http://suo.ieee.org/ontology/msg04052.html http://web.archive.org/web/20110612010724/http://suo.ieee.org/ontology/msg04054.html http://web.archive.org/web/20110612000847/http://suo.ieee.org/ontology/msg04055.html http://web.archive.org/web/20110612001959/http://suo.ieee.org/ontology/msg04067.html http://web.archive.org/web/20110612010507/http://suo.ieee.org/ontology/msg04068.html http://web.archive.org/web/20110612002014/http://suo.ieee.org/ontology/msg04069.html http://web.archive.org/web/20110612010701/http://suo.ieee.org/ontology/msg04070.html http://web.archive.org/web/20110612003540/http://suo.ieee.org/ontology/msg04072.html http://web.archive.org/web/20110612005229/http://suo.ieee.org/ontology/msg04073.html http://web.archive.org/web/20110610153117/http://suo.ieee.org/ontology/msg04074.html http://web.archive.org/web/20110612010555/http://suo.ieee.org/ontology/msg04077.html http://web.archive.org/web/20110612001918/http://suo.ieee.org/ontology/msg04079.html http://web.archive.org/web/20110612005244/http://suo.ieee.org/ontology/msg04080.html http://web.archive.org/web/20110612005249/http://suo.ieee.org/ontology/msg04268.html http://web.archive.org/web/20110612010626/http://suo.ieee.org/ontology/msg04269.html http://web.archive.org/web/20110612000853/http://suo.ieee.org/ontology/msg04272.html http://web.archive.org/web/20110612010514/http://suo.ieee.org/ontology/msg04273.html http://web.archive.org/web/20110612002235/http://suo.ieee.org/ontology/msg04290.html Inquiry List (May–Jul 2004) http://stderr.org/pipermail/inquiry/2004-May/thread.html#1400 http://stderr.org/pipermail/inquiry/2004-July/thread.html#1685 http://stderr.org/pipermail/inquiry/2004-May/001400.html http://stderr.org/pipermail/inquiry/2004-May/001401.html http://stderr.org/pipermail/inquiry/2004-May/001402.html http://stderr.org/pipermail/inquiry/2004-May/001403.html http://stderr.org/pipermail/inquiry/2004-May/001404.html http://stderr.org/pipermail/inquiry/2004-May/001405.html http://stderr.org/pipermail/inquiry/2004-May/001406.html http://stderr.org/pipermail/inquiry/2004-May/001407.html http://stderr.org/pipermail/inquiry/2004-May/001408.html http://stderr.org/pipermail/inquiry/2004-May/001410.html http://stderr.org/pipermail/inquiry/2004-May/001411.html http://stderr.org/pipermail/inquiry/2004-May/001412.html http://stderr.org/pipermail/inquiry/2004-May/001413.html http://stderr.org/pipermail/inquiry/2004-May/001415.html http://stderr.org/pipermail/inquiry/2004-May/001416.html http://stderr.org/pipermail/inquiry/2004-May/001418.html http://stderr.org/pipermail/inquiry/2004-May/001419.html http://stderr.org/pipermail/inquiry/2004-May/001420.html http://stderr.org/pipermail/inquiry/2004-May/001421.html http://stderr.org/pipermail/inquiry/2004-May/001422.html http://stderr.org/pipermail/inquiry/2004-May/001423.html http://stderr.org/pipermail/inquiry/2004-May/001424.html http://stderr.org/pipermail/inquiry/2004-July/001685.html http://stderr.org/pipermail/inquiry/2004-July/001686.html http://stderr.org/pipermail/inquiry/2004-July/001687.html http://stderr.org/pipermail/inquiry/2004-July/001688.html NKS Forum (May–Jul 2004) http://forum.wolframscience.com/archive/topic/420.html http://forum.wolframscience.com/printthread.php?threadid=420 http://forum.wolframscience.com/showthread.php?threadid=420 http://forum.wolframscience.com/showthread.php?postid=1282#post1282 http://forum.wolframscience.com/showthread.php?postid=1285#post1285 http://forum.wolframscience.com/showthread.php?postid=1289#post1289 http://forum.wolframscience.com/showthread.php?postid=1292#post1292 http://forum.wolframscience.com/showthread.php?postid=1293#post1293 http://forum.wolframscience.com/showthread.php?postid=1294#post1294 http://forum.wolframscience.com/showthread.php?postid=1296#post1296 http://forum.wolframscience.com/showthread.php?postid=1299#post1299 http://forum.wolframscience.com/showthread.php?postid=1301#post1301 http://forum.wolframscience.com/showthread.php?postid=1304#post1304 http://forum.wolframscience.com/showthread.php?postid=1307#post1307 http://forum.wolframscience.com/showthread.php?postid=1309#post1309 http://forum.wolframscience.com/showthread.php?postid=1311#post1311 http://forum.wolframscience.com/showthread.php?postid=1314#post1314 http://forum.wolframscience.com/showthread.php?postid=1315#post1315 http://forum.wolframscience.com/showthread.php?postid=1318#post1318 http://forum.wolframscience.com/showthread.php?postid=1321#post1321 http://forum.wolframscience.com/showthread.php?postid=1323#post1323 http://forum.wolframscience.com/showthread.php?postid=1326#post1326 http://forum.wolframscience.com/showthread.php?postid=1327#post1327 http://forum.wolframscience.com/showthread.php?postid=1330#post1330 http://forum.wolframscience.com/showthread.php?postid=1331#post1331 http://forum.wolframscience.com/showthread.php?postid=1598#post1598 http://forum.wolframscience.com/showthread.php?postid=1601#post1601 http://forum.wolframscience.com/showthread.php?postid=1602#post1602 http://forum.wolframscience.com/showthread.php?postid=1603#post1603