Difference between revisions of "User:Jon Awbrey/GRAPHICS"
Jon Awbrey (talk | contribs) (→Analysis of contingent propositions: table of unscaled figs) |
Jon Awbrey (talk | contribs) (→Analysis of contingent propositions: tables of thin line figs : unscaled & scaled) |
||
| Line 820: | Line 820: | ||
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-0.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-1.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-2.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-3.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-4.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-5.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-6.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-7.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-8.jpg]] |
|- | |- | ||
| − | | [[Image: | + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-9.jpg]] |
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" cellpadding="8" style="text-align:center" | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-0.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-1.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-2.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-3.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-4.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-5.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-6.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-7.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-8.jpg|500px]] | ||
| + | |- | ||
| + | | [[Image:Proof (P (Q)) (P (R)) = (P (Q R)) 2-1-9.jpg|500px]] | ||
|} | |} | ||
Revision as of 11:50, 18 August 2009
Cactus Graphs
Hi Res
|
117 px → 20 px |
|
117 px → 20 px |
|
117 px → 20 px |
_Big.jpg){kind=small}
|
117 px → 20 px |
|
290 px → 50 px |
(B)(C))_Big.jpg)
|
386 px → 65 px |
B_Big.jpg){kind=small}
|
204 px → 35 px |
)_Big.jpg)
|
348 px → 60 px |
_Big.jpg)
|
386 px → 65 px |
)_Big.jpg)
|
386 px → 65 px |
_Big.jpg)
|
386 px → 65 px |
,(B),(C))_Big.jpg)
|
386 px → 65 px |
)_Big.jpg)
|
386 px → 65 px |
,(B),(C)))_Big.jpg)
|
386 px → 65 px |
,(C))_Big.jpg)
|
386 px → 65 px |
,B,C))_Big.jpg)
|
386 px → 65 px |
)_Big.jpg)
|
530 px → 90 px |
,(B),(C))_Big.jpg)
|
530 px → 90 px |
Lo Res
|
|
|
|
Differential Logic
ASCII Graphics
Series 1
o-------------------------------------------------o | | | | | o-------------o o-------------o | | / \ / \ | | / o \ | | / /%\ \ | | / /%%%\ \ | | o o%%%%%o o | | | |%%%%%| | | | | P |%%%%%| Q | | | | |%%%%%| | | | o o%%%%%o o | | \ \%%%/ / | | \ \%/ / | | \ o / | | \ / \ / | | o-------------o o-------------o | | | | | o-------------------------------------------------o | f = p q | o-------------------------------------------------o Figure 22-a. Conjunction pq : X -> B |
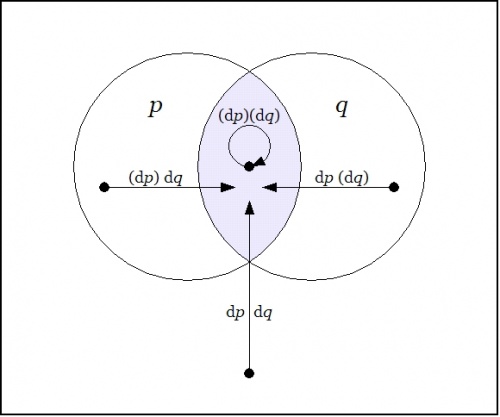
o-------------------------------------------------o | | | | | o-------------o o-------------o | | / \ / \ | | / P o Q \ | | / /%\ \ | | / /%%%\ \ | | o o.->-.o o | | | p(q)(dp)dq |%\%/%| (p)q dp(dq) | | | | o---------------|->o<-|---------------o | | | | |%%^%%| | | | o o%%|%%o o | | \ \%|%/ / | | \ \|/ / | | \ o / | | \ /|\ / | | o-------------o | o-------------o | | | | | | | | | | | o | | (p)(q) dp dq | | | o-------------------------------------------------o | f = p q | o-------------------------------------------------o | | | Ef = p q (dp)(dq) | | | | + p (q) (dp) dq | | | | + (p) q dp (dq) | | | | + (p)(q) dp dq | | | o-------------------------------------------------o Figure 22-b. Enlargement E[pq] : EX -> B |
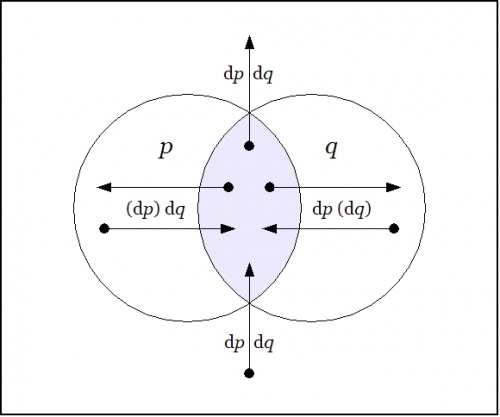
o-------------------------------------------------o | | | | | o-------------o o-------------o | | / \ / \ | | / P o Q \ | | / /%\ \ | | / /%%%\ \ | | o o%%%%%o o | | | (dp)dq |%%%%%| dp(dq) | | | | o<--------------|->o<-|-------------->o | | | | |%%^%%| | | | o o%%|%%o o | | \ \%|%/ / | | \ \|/ / | | \ o / | | \ /|\ / | | o-------------o | o-------------o | | | | | | | | v | | o | | dp dq | | | o-------------------------------------------------o | f = p q | o-------------------------------------------------o | | | Df = p q ((dp)(dq)) | | | | + p (q) (dp) dq | | | | + (p) q dp (dq) | | | | + (p)(q) dp dq | | | o-------------------------------------------------o Figure 22-c. Difference D[pq] : EX -> B |
o---------------------------------------------------------------------o | | | X | | o-------------------o | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | o o | | | | | | | | | | | | | | | G | | | | | | | | | | | | | | | o o | | \ / | | \ / | | \ T / | | \ o<------------/-------------o | | \ / | | \ / | | \ / | | o-------------------o | | | | | o---------------------------------------------------------------------o Figure 23. Elements of a Cybernetic System |
Series 2
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / /%\ \ | | / /%%%\ \ | | / /%%%%%\ \ | | / /%%%%%%%\ \ | | / /%%%%%%%%%\ \ | | o o%%%%%%%%%%%o o | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | | P |%%%%%%%%%%%| Q | | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | o o%%%%%%%%%%%o o | | \ \%%%%%%%%%/ / | | \ \%%%%%%%/ / | | \ \%%%%%/ / | | \ \%%%/ / | | \ \%/ / | | \ o / | | \ / \ / | | o-------------------o o-------------------o | | | | | o---------------------------------------------------------------------o Figure 24-1. Proposition pq : X -> B |
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (dp) (dq) o o | | | | o-->--o | | | | | | \ / | | | | | (dp) dq | \ / | dp (dq) | | | | o<-----------------o----------------->o | | | | | | | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | dp | dq | | | | | v | | o | | | o---------------------------------------------------------------------o Figure 24-2. Tacit Extension !e![pq] : EX -> B |
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (dp) (dq) o o | | | | o-->--o | | | | | | \ / | | | | | (dp) dq | \ / | dp (dq) | | | | o----------------->o<-----------------o | | | | | ^ | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | dp | dq | | | | | | | | o | | | o---------------------------------------------------------------------o Figure 25-1. Enlargement E[pq] : EX -> B |
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o o o | | | | | | | | | | | | | | | (dp) dq | | dp (dq) | | | | o<---------------->o<---------------->o | | | | | ^ | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | dp | dq | | | | | v | | o | | | o---------------------------------------------------------------------o Figure 25-2. Difference Map D[pq] : EX -> B |
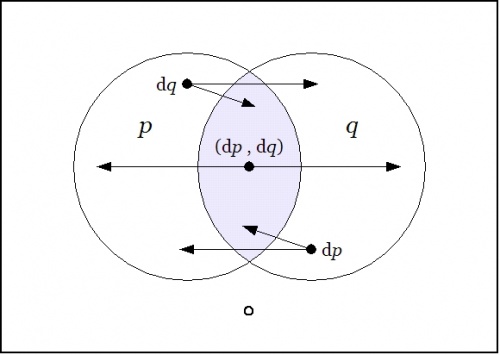
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / o \ \ | | / / ^ ^ \ \ | | o o / \ o o | | | | / \ | | | | | | / \ | | | | | |/ \| | | | | (dp)/ dq dp \(dq) | | | | /| |\ | | | | / | | \ | | | | / | | \ | | | o / o o \ o | | \ v \ dp dq / v / | | \ o<--------------------->o / | | \ \ / / | | \ \ / / | | \ \ / / | | \ o / | | \ / \ / | | o-------------------o o-------------------o | | | | | o---------------------------------------------------------------------o Figure 26-1. Differential or Tangent d[pq] : EX -> B |
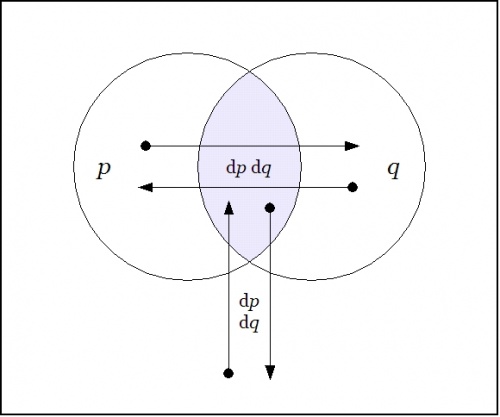
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o o o | | | | | | | | | | | | | | | | dp dq | | | | | o<------------------------------->o | | | | | | | | | | | | | | | | | o | | | | o o ^ o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ dp | dq / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | | | | | | | v | | o | | | o---------------------------------------------------------------------o Figure 26-2. Remainder r[pq] : EX -> B |
JPEG Graphics
Series 1
|
| \(\text{Figure 22-a. Conjunction}~ pq : X \to \mathbb{B}\) |
|
| \(\text{Figure 22-b. Enlargement}~ \operatorname{E}(pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \operatorname{E}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \end{array}\) |
|
| \(\text{Figure 22-c. Difference}~ \operatorname{D}(pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \operatorname{D}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(}q \texttt{)} & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \end{array}\) |
Series 2
|
|
| \(\text{Figure 24-1. Proposition}~ pq : X \to \mathbb{B}\) |
|
| \(\text{Figure 24-2. Tacit Extension}~ \varepsilon (pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \varepsilon (pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \\[4pt] & + & p & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \end{array}\) |
|
|
| \(\text{Figure 25-1. Enlargement Map}~ \operatorname{E}(pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \operatorname{E}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \end{array}\) |
|
|
| \(\text{Figure 25-2. Difference Map}~ \operatorname{D}(pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \operatorname{D}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(}q \texttt{)} & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \end{array}\) |
|
| \(\text{Figure 26-1. Tangent Map}~ \operatorname{d}(pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \operatorname{d}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{,} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \operatorname{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \operatorname{d}p \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & 0 \end{array}\) |
|
| \(\text{Figure 26-2. Remainder Map}~ \operatorname{r}(pq) : \operatorname{E}X \to \mathbb{B}\) |
|
\(\begin{array}{rcccccc} \operatorname{r}(pq) & = & p & \cdot & q & \cdot & \operatorname{d}p ~ \operatorname{d}q \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \operatorname{d}p ~ \operatorname{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \operatorname{d}p ~ \operatorname{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \operatorname{d}p ~ \operatorname{d}q \end{array}\) |
Propositional Equation Reasoning Systems
Analysis of contingent propositions
)_(P_(R)).jpg) |
(26) |
)_(P_(R)).jpg) |
(27) |
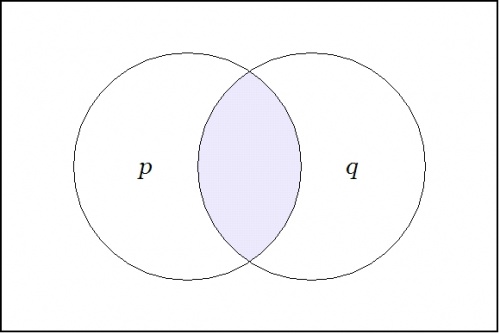
| \(\text{Venn Diagram for}~ \texttt{(} p \texttt{~(} q \texttt{))~(} p \texttt{~(} r \texttt{))}\) |
).jpg) |
(28) |
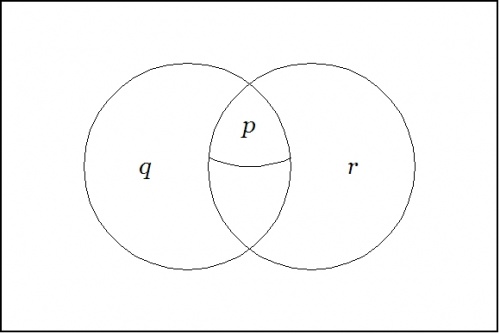
| \(\text{Venn Diagram for}~ \texttt{(} p \texttt{~(} q ~ r \texttt{))}\) |
)_(P_(R))_%3D_(P_(Q_R)).jpg) |
(29) |
)_(P_(R))_%3D_(P_(Q_R))_Proof_1.jpg)
|
(30) |
)_(P_(R))_%3D_(P_(Q_R))_Proof_2a_Alt.jpg)
|
(31) |
)_(P_(R))_%3D_(P_(Q_R))_2-1-0.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-1.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-2.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-3.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-4.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-5.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-6.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-7.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-8.jpg)
|
)_(P_(R))_%3D_(P_(Q_R))_2-1-9.jpg)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
