User:Jon Awbrey/GRAPHICS

Image Gallery

Reduction 6:1

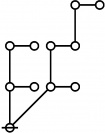
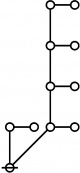
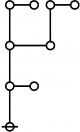
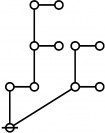
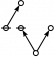
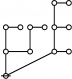
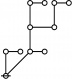
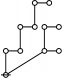
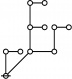
Cacti

Image	Scale
	117 px → 20 px
	117 px → 20 px

Riffs

Image	Scale
	117 px → 20 px
	240 px → 40 px
	233 px → 40 px
	384 px → 65 px
	384 px → 65 px
	377 px → 65 px
	384 px → 65 px
	240 px → 40 px
	528 px → 90 px
	528 px → 90 px
	384 px → 65 px
	384 px → 65 px
	521 px → 90 px
	528 px → 90 px
	377 px → 65 px
	521 px → 90 px
	384 px → 65 px
	528 px → 90 px
	528 px → 90 px
	521 px → 90 px
	672 px → 115 px
	384 px → 65 px
	672 px → 115 px
	384 px → 65 px
	528 px → 90 px
	384 px → 65 px
	521 px → 90 px
	528 px → 90 px
	672 px → 115 px
	672 px → 115 px
	528 px → 90 px
	672 px → 115 px
	665 px → 115 px
	521 px → 90 px
	384 px → 65 px
	384 px → 65 px
	672 px → 115 px

Rotes

Image	Scale
	117 px → 20 px
	233 px → 40 px
	233 px → 40 px
	377 px → 65 px
	233 px → 40 px
	473 px → 80 px
	377 px → 65 px
	377 px → 65 px
	473 px → 80 px
	473 px → 80 px
	233 px → 40 px
	617 px → 105 px
	473 px → 80 px
	617 px → 105 px
	473 px → 80 px
	521 px → 90 px
	377 px → 65 px
	713 px → 120 px
	377 px → 65 px
	617 px → 105 px
	617 px → 105 px
	473 px → 80 px
	473 px → 80 px
	617 px → 105 px
	473 px → 80 px
	713 px → 120 px
	473 px → 80 px
	761 px → 130 px
	473 px → 80 px
	713 px → 120 px
	233 px → 40 px
	377 px → 65 px
	473 px → 80 px
	617 px → 105 px
	617 px → 105 px
	857 px → 145 px
	617 px → 105 px
	617 px → 105 px
	713 px → 120 px
	617 px → 105 px
	473 px → 80 px
	857 px → 145 px
	617 px → 105 px
	617 px → 105 px
	713 px → 120 px
	713 px → 120 px
	473 px → 80 px
	617 px → 105 px
	473 px → 80 px
	713 px → 120 px
	617 px → 105 px
	857 px → 145 px
	521 px → 90 px
	713 px → 120 px
	473 px → 80 px
	761 px → 130 px
	617 px → 105 px
	713 px → 120 px
	377 px → 65 px
	905 px → 155 px
	1001 px → 170 px

Reduction 10:1

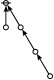
Cacti

Image	Scale
	117 px → 12 px
	117 px → 12 px

Riffs

Image	Scale
	117 px → 12 px
	240 px → 24 px
	233 px → 24 px
	384 px → 38 px
	384 px → 38 px
	377 px → 38 px
	384 px → 38 px
	240 px → 24 px
	528 px → 54 px
	528 px → 54 px
	384 px → 38 px
	384 px → 38 px
	521 px → 54 px
	528 px → 54 px
	377 px → 38 px
	521 px → 54 px
	384 px → 38 px
	528 px → 54 px
	528 px → 54 px
	521 px → 54 px
	672 px → 68 px
	384 px → 38 px
	672 px → 68 px
	384 px → 38 px
	528 px → 54 px
	384 px → 38 px
	521 px → 54 px
	528 px → 54 px
	672 px → 68 px
	672 px → 68 px
	528 px → 54 px
	672 px → 68 px
	665 px → 68 px
	521 px → 54 px
	384 px → 38 px
	384 px → 38 px
	672 px → 68 px

Rotes

Image	Scale
	117 px → 12 px
	233 px → 24 px
	233 px → 24 px
	377 px → 38 px
	233 px → 24 px
	473 px → 48 px
	377 px → 38 px
	377 px → 38 px
	473 px → 48 px
	473 px → 48 px
	233 px → 24 px
	617 px → 62 px
	473 px → 48 px
	617 px → 62 px
	473 px → 48 px
	521 px → 52 px
	377 px → 38 px
	713 px → 72 px
	377 px → 38 px
	617 px → 62 px
	617 px → 62 px
	473 px → 48 px
	473 px → 48 px
	617 px → 62 px
	473 px → 48 px
	713 px → 72 px
	473 px → 48 px
	761 px → 76 px
	473 px → 48 px
	713 px → 72 px
	233 px → 24 px
	377 px → 38 px
	473 px → 48 px
	617 px → 62 px
	617 px → 62 px
	857 px → 86 px
	617 px → 62 px
	617 px → 62 px
	713 px → 72 px
	617 px → 62 px
	473 px → 48 px
	857 px → 86 px
	617 px → 62 px
	617 px → 62 px
	713 px → 72 px
	713 px → 72 px
	473 px → 48 px
	617 px → 62 px
	473 px → 48 px
	713 px → 72 px
	617 px → 62 px
	857 px → 86 px
	521 px → 52 px
	713 px → 72 px
	473 px → 48 px
	761 px → 76 px
	617 px → 62 px
	713 px → 72 px
	377 px → 38 px
	905 px → 90 px
	1001 px → 100 px

Riffs in Numerical Order

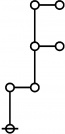
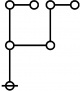
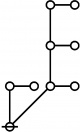
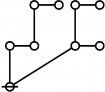
$\text{Riffs in Numerical Order}\!$

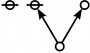
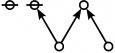
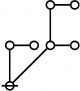
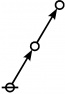
$\begin{array}{l} \varnothing \\ 1 \end{array}$	$\text{p}\!$ $\begin{array}{l} 1\!:\!1 \\ 2 \end{array}$	$\text{p}_\text{p}\!$ $\begin{array}{l} 2\!:\!1 \\ 3 \end{array}$	$\text{p}^\text{p}\!$ $\begin{array}{l} 1\!:\!2 \\ 4 \end{array}$	$\text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 3\!:\!1 \\ 5 \end{array}$
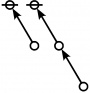
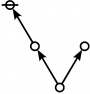
$\text{p} \text{p}_\text{p}\!$ $\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}$	$\text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 4\!:\!1 \\ 7 \end{array}$	$\text{p}^{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!3 \\ 8 \end{array}$	$\text{p}_\text{p}^\text{p}\!$ $\begin{array}{l} 2\!:\!2 \\ 9 \end{array}$	$\text{p} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}$
$\text{p}_{\text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 5\!:\!1 \\ 11 \end{array}$	$\text{p}^\text{p} \text{p}_\text{p}\!$ $\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}$	$\text{p}_{\text{p} \text{p}_\text{p}}\!$ $\begin{array}{l} 6\!:\!1 \\ 13 \end{array}$	$\text{p} \text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}$	$\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}$
$\text{p}^{\text{p}^\text{p}}\!$ $\begin{array}{l} 1\!:\!4 \\ 16 \end{array}$	$\text{p}_{\text{p}_{\text{p}^\text{p}}}\!$ $\begin{array}{l} 7\!:\!1 \\ 17 \end{array}$	$\text{p} \text{p}_\text{p}^\text{p}\!$ $\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}$	$\text{p}_{\text{p}^{\text{p}_\text{p}}}\!$ $\begin{array}{l} 8\!:\!1 \\ 19 \end{array}$	$\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}$
$\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}$	$\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}$	$\text{p}_{\text{p}_\text{p}^\text{p}}\!$ $\begin{array}{l} 9\!:\!1 \\ 23 \end{array}$	$\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!$ $\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}$	$\text{p}_{\text{p}_\text{p}}^\text{p}\!$ $\begin{array}{l} 3\!:\!2 \\ 25 \end{array}$
$\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}$	$\text{p}_\text{p}^{\text{p}_\text{p}}\!$ $\begin{array}{l} 2\!:\!3 \\ 27 \end{array}$	$\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}$	$\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 10\!:\!1 \\ 29 \end{array}$	$\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}$
$\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!$ $\begin{array}{l} 11\!:\!1 \\ 31 \end{array}$	$\text{p}^{\text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 1\!:\!5 \\ 32 \end{array}$	$\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}$	$\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}$	$\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}$
$\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!$ $\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}$	$\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!$ $\begin{array}{l} 12\!:\!1 \\ 37 \end{array}$	$\cdots$ $\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}$	$\cdots$ $\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!$ $\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}$	$\cdots$ $\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}$
$\cdots$ $\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!$ $\begin{array}{l} 13\!:\!1 \\ 41 \end{array}$	$\cdots$ $\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}$	$\cdots$ $\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!$ $\begin{array}{l} 14\!:\!1 \\ 43 \end{array}$	$\cdots$ $\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}$	$\cdots$ $\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}$
$\cdots$ $\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}$	$\cdots$ $\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 15\!:\!1 \\ 47 \end{array}$	$\cdots$ $\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!$ $\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}$	$\cdots$ $\text{p}_{\text{p}^\text{p}}^\text{p}\!$ $\begin{array}{l} 4\!:\!2 \\ 49 \end{array}$	$\cdots$ $\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!$ $\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}$
$\cdots$ $\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!$ $\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}$	$\cdots$ $\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}$	$\cdots$ $\text{p}_{\text{p}^{\text{p}^\text{p}}}\!$ $\begin{array}{l} 16\!:\!1 \\ 53 \end{array}$	$\cdots$ $\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}$	$\cdots$ $\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}$
$\cdots$ $\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!$ $\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}$	$\cdots$ $\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!$ $\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}$	$\cdots$ $\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!$ $\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}$	$\cdots$ $\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!$ $\begin{array}{l} 17\!:\!1 \\ 59 \end{array}$	$\cdots$ $\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!$ $\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}$

Rotes in Numerical Order

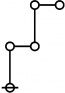
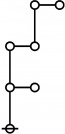
$\begin{array}{l} \varnothing \\ 1 \end{array}$	$\begin{array}{l} 1\!:\!1 \\ 2 \end{array}$	$\begin{array}{l} 2\!:\!1 \\ 3 \end{array}$	$\begin{array}{l} 1\!:\!2 \\ 4 \end{array}$	$\begin{array}{l} 3\!:\!1 \\ 5 \end{array}$
$\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}$	$\begin{array}{l} 4\!:\!1 \\ 7 \end{array}$	$\begin{array}{l} 1\!:\!3 \\ 8 \end{array}$	$\begin{array}{l} 2\!:\!2 \\ 9 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}$
$\begin{array}{l} 5\!:\!1 \\ 11 \end{array}$	$\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}$	$\begin{array}{l} 6\!:\!1 \\ 13 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}$	$\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}$
$\begin{array}{l} 1\!:\!4 \\ 16 \end{array}$	$\begin{array}{l} 7\!:\!1 \\ 17 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}$	$\begin{array}{l} 8\!:\!1 \\ 19 \end{array}$	$\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}$
$\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}$	$\begin{array}{l} 9\!:\!1 \\ 23 \end{array}$	$\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}$	$\begin{array}{l} 3\!:\!2 \\ 25 \end{array}$
$\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}$	$\begin{array}{l} 2\!:\!3 \\ 27 \end{array}$	$\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}$	$\begin{array}{l} 10\!:\!1 \\ 29 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}$
$\begin{array}{l} 11\!:\!1 \\ 31 \end{array}$	$\begin{array}{l} 1\!:\!5 \\ 32 \end{array}$	$\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}$	$\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}$
$\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}$	$\begin{array}{l} 12\!:\!1 \\ 37 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}$	$\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}$	$\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}$
$\begin{array}{l} 13\!:\!1 \\ 41 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}$	$\begin{array}{l} 14\!:\!1 \\ 43 \end{array}$	$\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}$	$\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}$
$\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}$	$\begin{array}{l} 15\!:\!1 \\ 47 \end{array}$	$\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}$	$\begin{array}{l} 4\!:\!2 \\ 49 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}$
$\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}$	$\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}$	$\begin{array}{l} 16\!:\!1 \\ 53 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}$	$\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}$
$\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}$	$\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}$	$\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}$	$\begin{array}{l} 17\!:\!1 \\ 59 \end{array}$	$\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}$

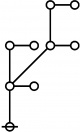
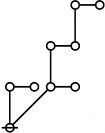
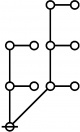
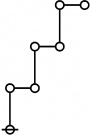
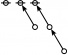
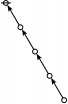
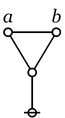
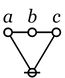
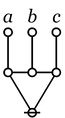
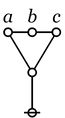
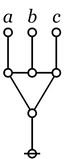
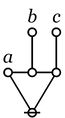
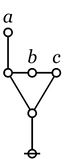
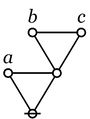
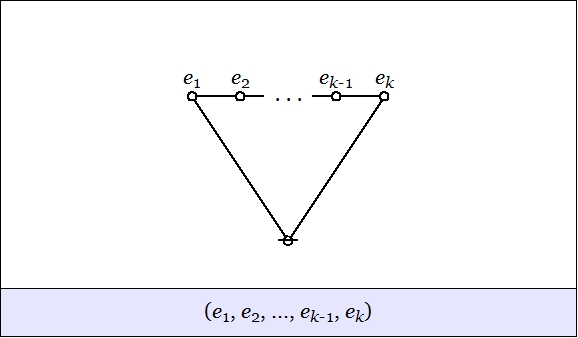
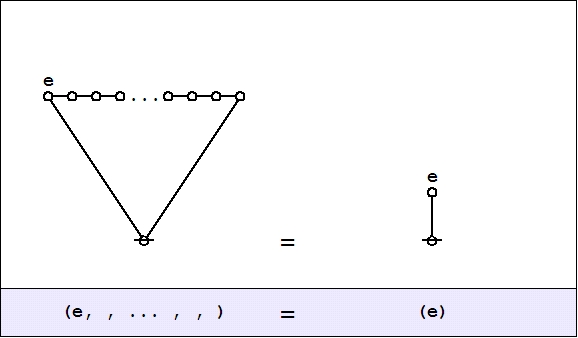
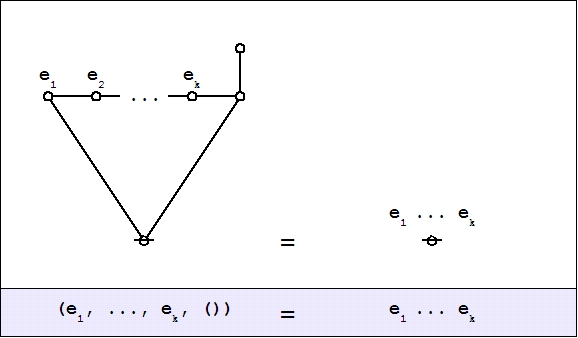
Cactus Graphs

Hi Res

	117 px → 20 px
	117 px → 20 px
	117 px → 20 px
	117 px → 20 px
	290 px → 50 px
	386 px → 65 px
	204 px → 35 px
	348 px → 60 px
	386 px → 65 px
	386 px → 65 px
	386 px → 65 px
	386 px → 65 px
	386 px → 65 px
	386 px → 65 px
	386 px → 65 px
	386 px → 65 px
	530 px → 90 px
	530 px → 90 px

Lo Res

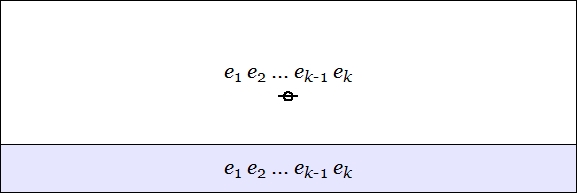
Differential Logic

ASCII Graphics

Series 1

o-------------------------------------------------o | | | | | o-------------o o-------------o | | / \ / \ | | / o \ | | / /%\ \ | | / /%%%\ \ | | o o%%%%%o o | | | |%%%%%| | | | | P |%%%%%| Q | | | | |%%%%%| | | | o o%%%%%o o | | \ \%%%/ / | | \ \%/ / | | \ o / | | \ / \ / | | o-------------o o-------------o | | | | | o-------------------------------------------------o | f = p q | o-------------------------------------------------o Figure 22-a. Conjunction pq : X -> B

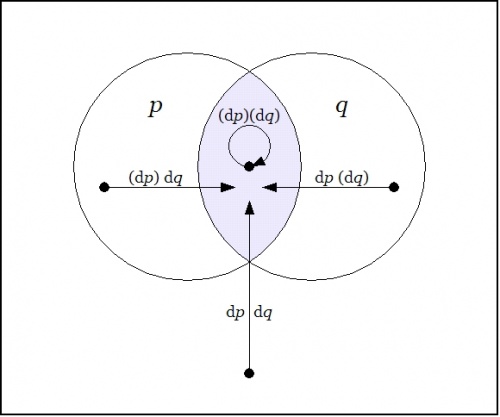
o-------------------------------------------------o | | | | | o-------------o o-------------o | | / \ / \ | | / P o Q \ | | / /%\ \ | | / /%%%\ \ | | o o.->-.o o | | | p(q)(dp)dq |%\%/%| (p)q dp(dq) | | | | o---------------|->o<-|---------------o | | | | |%%^%%| | | | o o%%|%%o o | | \ \%|%/ / | | \ \|/ / | | \ o / | | \ /|\ / | | o-------------o | o-------------o | | | | | | | | | | | o | | (p)(q) dp dq | | | o-------------------------------------------------o | f = p q | o-------------------------------------------------o | | | Ef = p q (dp)(dq) | | | | + p (q) (dp) dq | | | | + (p) q dp (dq) | | | | + (p)(q) dp dq | | | o-------------------------------------------------o Figure 22-b. Enlargement E[pq] : EX -> B

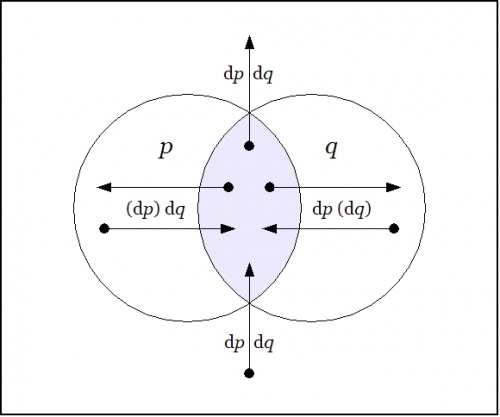
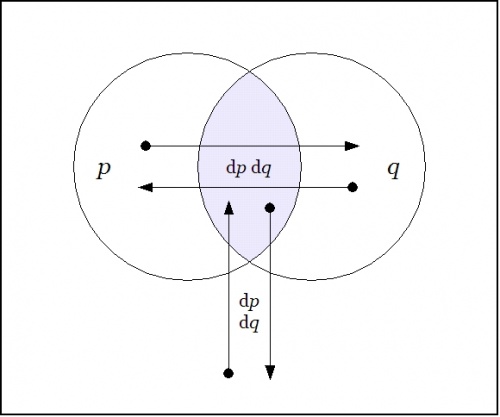
o-------------------------------------------------o | | | | | o-------------o o-------------o | | / \ / \ | | / P o Q \ | | / /%\ \ | | / /%%%\ \ | | o o%%%%%o o | | | (dp)dq |%%%%%| dp(dq) | | | | o<--------------|->o<-|-------------->o | | | | |%%^%%| | | | o o%%|%%o o | | \ \%|%/ / | | \ \|/ / | | \ o / | | \ /|\ / | | o-------------o | o-------------o | | | | | | | | v | | o | | dp dq | | | o-------------------------------------------------o | f = p q | o-------------------------------------------------o | | | Df = p q ((dp)(dq)) | | | | + p (q) (dp) dq | | | | + (p) q dp (dq) | | | | + (p)(q) dp dq | | | o-------------------------------------------------o Figure 22-c. Difference D[pq] : EX -> B

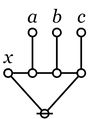
o---------------------------------------------------------------------o | | | X | | o-------------------o | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | o o | | | | | | | | | | | | | | | G | | | | | | | | | | | | | | | o o | | \ / | | \ / | | \ T / | | \ o<------------/-------------o | | \ / | | \ / | | \ / | | o-------------------o | | | | | o---------------------------------------------------------------------o Figure 23. Elements of a Cybernetic System

Series 2

o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / /%\ \ | | / /%%%\ \ | | / /%%%%%\ \ | | / /%%%%%%%\ \ | | / /%%%%%%%%%\ \ | | o o%%%%%%%%%%%o o | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | | P |%%%%%%%%%%%| Q | | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | | |%%%%%%%%%%%| | | | o o%%%%%%%%%%%o o | | \ \%%%%%%%%%/ / | | \ \%%%%%%%/ / | | \ \%%%%%/ / | | \ \%%%/ / | | \ \%/ / | | \ o / | | \ / \ / | | o-------------------o o-------------------o | | | | | o---------------------------------------------------------------------o Figure 24-1. Proposition pq : X -> B

o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (dp) (dq) o o | | | | o-->--o | | | | | | \ / | | | | | (dp) dq | \ / | dp (dq) | | | | o<-----------------o----------------->o | | | | | | | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | dp | dq | | | | | v | | o | | | o---------------------------------------------------------------------o Figure 24-2. Tacit Extension !e![pq] : EX -> B

o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (dp) (dq) o o | | | | o-->--o | | | | | | \ / | | | | | (dp) dq | \ / | dp (dq) | | | | o----------------->o<-----------------o | | | | | ^ | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | dp | dq | | | | | | | | o | | | o---------------------------------------------------------------------o Figure 25-1. Enlargement E[pq] : EX -> B

o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o o o | | | | | | | | | | | | | | | (dp) dq | | dp (dq) | | | | o<---------------->o<---------------->o | | | | | ^ | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | dp | dq | | | | | v | | o | | | o---------------------------------------------------------------------o Figure 25-2. Difference Map D[pq] : EX -> B

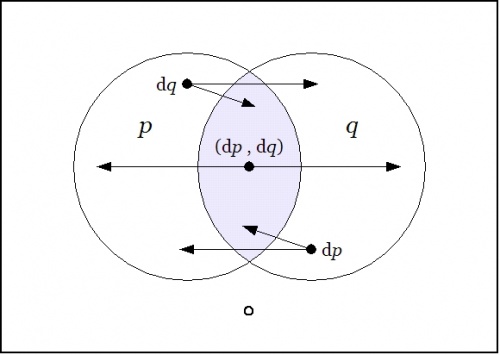
o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / o \ \ | | / / ^ ^ \ \ | | o o / \ o o | | | | / \ | | | | | | / \ | | | | | |/ \| | | | | (dp)/ dq dp \(dq) | | | | /| |\ | | | | / | | \ | | | | / | | \ | | | o / o o \ o | | \ v \ dp dq / v / | | \ o<--------------------->o / | | \ \ / / | | \ \ / / | | \ \ / / | | \ o / | | \ / \ / | | o-------------------o o-------------------o | | | | | o---------------------------------------------------------------------o Figure 26-1. Differential or Tangent d[pq] : EX -> B

o---------------------------------------------------------------------o | | | X | | o-------------------o o-------------------o | | / \ / \ | | / P o Q \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o o o | | | | | | | | | | | | | | | | dp dq | | | | | o<------------------------------->o | | | | | | | | | | | | | | | | | o | | | | o o ^ o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ dp | dq / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | | | | | | | v | | o | | | o---------------------------------------------------------------------o Figure 26-2. Remainder r[pq] : EX -> B

JPEG Graphics

Series 1

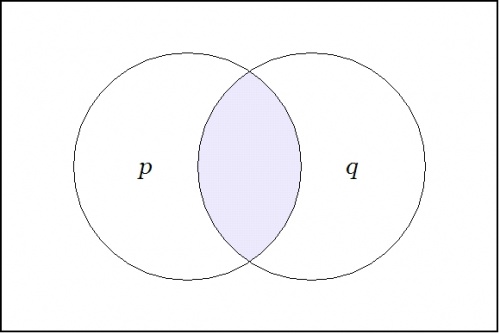
$\text{Figure 22-a. Conjunction}~ pq : X \to \mathbb{B}$

$\text{Figure 22-b. Enlargement}~ \operatorname{E}(pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \operatorname{E}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \end{array}$

$\text{Figure 22-c. Difference}~ \operatorname{D}(pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \operatorname{D}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(}q \texttt{)} & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \end{array}$

Series 2

$\text{Figure 24-1. Proposition}~ pq : X \to \mathbb{B}$

$\text{Figure 24-2. Tacit Extension}~ \varepsilon (pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \varepsilon (pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \\[4pt] & + & p & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \end{array}$

$\text{Figure 25-1. Enlargement Map}~ \operatorname{E}(pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \operatorname{E}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \end{array}$

$\text{Figure 25-2. Difference Map}~ \operatorname{D}(pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \operatorname{D}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \texttt{(} \operatorname{d}p \texttt{)} \texttt{(} \operatorname{d}q \texttt{)} \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \texttt{~} \texttt{(} \operatorname{d}p \texttt{)} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{(} \operatorname{d}q \texttt{)} \texttt{~} \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(}q \texttt{)} & \cdot & \texttt{~} \texttt{~} \operatorname{d}p \texttt{~} \texttt{~} \operatorname{d}q \texttt{~} \texttt{~} \end{array}$

$\text{Figure 26-1. Tangent Map}~ \operatorname{d}(pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \operatorname{d}(pq) & = & p & \cdot & q & \cdot & \texttt{(} \operatorname{d}p \texttt{,} \operatorname{d}q \texttt{)} \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \operatorname{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \operatorname{d}p \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & 0 \end{array}$

$\text{Figure 26-2. Remainder Map}~ \operatorname{r}(pq) : \operatorname{E}X \to \mathbb{B}$

$\begin{array}{rcccccc} \operatorname{r}(pq) & = & p & \cdot & q & \cdot & \operatorname{d}p ~ \operatorname{d}q \\[4pt] & + & p & \cdot & \texttt{(} q \texttt{)} & \cdot & \operatorname{d}p ~ \operatorname{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & q & \cdot & \operatorname{d}p ~ \operatorname{d}q \\[4pt] & + & \texttt{(} p \texttt{)} & \cdot & \texttt{(} q \texttt{)} & \cdot & \operatorname{d}p ~ \operatorname{d}q \end{array}$

Propositional Equation Reasoning Systems

Analysis of contingent propositions

(26)

	(27)
$\text{Venn Diagram for}~ \texttt{(} p \texttt{~(} q \texttt{))~(} p \texttt{~(} r \texttt{))}$

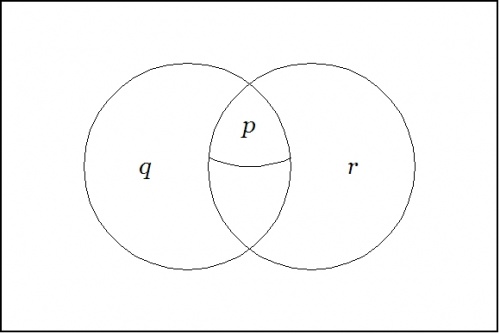	(28)
$\text{Venn Diagram for}~ \texttt{(} p \texttt{~(} q ~ r \texttt{))}$

(29)

Equation 1 : Proof 1

(30)

Equation 1 : Proof 2

Single Image Version

(31)

Serial Image Version

(31)

(33)

Equation 1 : Proof 3

Variant 1 start cast p dom can empty can cast q dom can dom spike can cast r can empty spike can

Variant 2 start cast p dom can empty can cast q can dom can spike can cast r can empty spike can

Variant 1

o-----------------------------------------------------------o | Equation E_1. Proof 3. | o-----------------------------------------------------------o | 1 | | q o o r q o r | | | | | | | p o o p p o | | \ / | | | o---------o | | \ / | | \ / | | \ / | | \ / | | o | | | | | | | | | | | | | | @ | | | o==================================< CAST "p" >=============o | 2 | | q r q r q r qr | | o o o o o o o o o | | | | | |/ |/ |/ | | o o o o o o | | \ / | \ / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | p o---------------o---o p | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o==================================< Domination >===========o | 3 | | q r q r | | o o o o o o | | | | | / / / | | o o o o o o | | \ / | \ / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | p o---------------o---o p | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o==================================< Cancellation >=========o | 4 | | q r q r | | o o o | | | | | | | o o o | | \ / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | p o---------------o---o p | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o==================================< Emptiness >============o | 5 | | q r q r | | o o o | | | | | | | o o o | | \ / | | | o-------o o | | \ / | | | \ / | | | \ / | | | o o | | | | | | | | | | | | | | p o---------------o---o p | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o==================================< Cancellation >=========o | 6 | | q r q r | | o o o | | | | | | | o o o | | \ / | | | o-------o | | \ / | | \ / | | \ / | | o | | | | | | | | | | | p o---------------o---o p | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o==================================< CAST "q" >=============o | 7 | | o o | | r r | r | | | o o o o o o r | | | | | | | | | | o o o o o o | | \ / | \ / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | q o---------------o---o q | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Domination >===========o | 8 | | o o | | r r | r | | | o o o o o o | | | | | | | | | | o o o o o o | | \ / | \ / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | q o---------------o---o q | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Cancellation >=========o | 9 | | r r r | | o o o | | | | | | | o o o o o | | / | \ / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | q o---------------o---o q | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Domination >===========o | 10 | | r r | | o o | | | | | | o o o o | | / | \ | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | q o---------------o---o q | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Spike >================o | 11 | | r r | | o o | | | | | | o o | | / | | | o-------o o | | \ / | | | \ / | | | \ / | | | o o | | | | | | | | | | | | | | q o---------------o---o q | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Cancellation >=========o | 12 | | r r | | o o | | | | | | o o | | / | | | o-------o | | \ / | | \ / | | \ / | | o | | | | | | | | | | | q o---------------o---o q | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< CAST "r" >=============o | 13 | | o o | | | | | | o o o o | | | | | | | | o o o o | | / | / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | r o---------------o---o r | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | q o-------o---o q | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Cancellation >=========o | 14 | | o o | | / | | | o-------o o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | | | | | | | | | | | | r o---------------o---o r | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | q o-------o---o q | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Emptiness & Spike >====o | 15 | | o o 16 | | | | | | | | | | | | | | o o | | | | | | | | | | | | | | r o---------------o---o r | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | q o-------o---o q | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< Cancellation >=========o | 17 | | r o-------o---o r | | \ / | | \ / | | \ / | | q o-------o---o q | | \ / | | \ / | | \ / | | p o-------o---o p | | \ / | | \ / | | \ / | | @ | | | o==================================< QED >==================o

(40)

Variant 2

(40)

Praeclarum Theorema : Proof by CAST

(23)